Miscellany 51: Apparent Wind Speed and True Wind Speed
Copyright © 2009, 2010 Joseph George Caldwell. All rights reserved. Posted at Internet website http://www.foundationwebsite.org. May be copied or reposted for non-commercial use, with attribution to author and website. (7 December 2009, revised 9 December 2009, minor edits 9 February 2010)
I recently spent a few days sailing with my brother on his sailboat off the east coast of the United States. He has a very nice sailboat, a Hunter 45-foot center-cockpit cruiser, that is equipped with all the latest features. The boat has a powerful guidance and control system, a Raymarine E Series system, that allows the pilot to chart his course on digital maps and then automatically steers the boat to follow the course, using the Global Positioning System (GPS).
The Raymarine system has a lot of features, including a radar tracking system. One of the features is a page that indicates various speeds, including ground wind speed (GWS), true wind speed (TWS), apparent wind speed (AWS), and speed over ground (SOG). My brother showed me this page, and during the time that I viewed it there was very little difference between the true wind speed and the apparent wind speed. This seemed strange, and so we consulted the Raymarine manual to see the definitions of the terms. They were not defined, and so my brother showed me two reference books that contained information on these terms: Chapman Piloting and Seamanship 64th edition by Elbert S. Maloney (Hearst Books / Sterling Publishing, 2003) and The Handbook of Sailing revised and updated by Bob Bond (Dorling Kindersley, 1992, 1980). While these books provided useful information on several of these terms, they did not define the term “ground wind speed,” and they did not explain calculation methods. We checked the Internet, and found a “True and Apparent Wind Calculator” at the US Sailing website, http://www.sailingusa.info/true_wind_calculator.htm. (Another true wind calculator is posted at http://www.starpathdemos.com/bowditch/table30.htm.) This website provides a detailed description on the methodology for calculating true and apparent wind speed. (Unfortunately, there is an error in the bottom right-hand panel, which is entitled, “Apparent-Wind Calculator Formulas”: the term “Apparent-Wind Degrees off the bow” should read “True-Wind Degrees off the bow”.)
The US Sailing website does not explain how the diagrams used to determine true and apparent wind speed were obtained. This note explains this.
The “apparent wind” is the wind that “appears” to you, whether you are moving (relative to the ground) or standing still (not moving relative to the ground). The “true wind” is the apparent wind while you are standing still. Wind speed is measured by an anemometer, and wind direction (the angle of the wind to the boat) is measured by a wind-direction indicator (e.g., burgee or tell-tale). (If the boat is not moving, these measurements are true wind speed and true wind angle; if the boat is moving, these measurements are apparent wind speed and apparent wind angle.)
It is noted that the sailor on the boat is always aware of the apparent wind speed and direction and the boat speed. The reason for wanting to know the true wind speed and direction is for recording in his log, or for reporting to other people (over the radio). The US Sailing wind-speed calculator can calculate true wind speed and direction from the apparent wind speed and direction (and boat speed), or the apparent wind speed and direction from the true wind speed and direction (and boat speed). It is not clear why or when one would wish to do the latter. The US Sailing website presents the following comment for its calculator:
“The true-wind is the apparent wind which you feel when you are not moving, for example at anchor. The apparent-wind is the wind direction and speed which you feel while the boat is moving. The apparent-wind is forward of the true-wind (except when it is directly forward or behind the boat). In a close reach, the apparent-wind is forward and is stronger than the true-wind. In a deep broad reach, the apparent-wind is forward and is weaker than the true-wind.”
To determine the relationship of apparent wind speed and true wind speed, we use the branch of physics called kinematics. The velocity of an object is defined by vector that is composed of a magnitude – the speed – and a direction. From the theory of kinematics it is known that all velocities are relative, and that velocities compose vectorially. We shall determine the relationship of apparent and true wind speeds by examining the vector diagram that describes the relationship between them. (For more details, see any book on elementary physics, such as Elements of Physics 2nd edition by George Shortley and Dudley Williams (Prentice-Hall, 1953, 1955).)
Since this problem relates to wind, and wind is the movement of air relative to the observer, it is easier to solve it by considering the motion of the boat (on which the observer is located), rather than the motion of the air. The reason for this is that the boat velocities (relative to a specified frame of reference) add vectorially, whereas the various wind speeds involved in this problem do not (since they are relative to different frames of reference, viz., the ground for true wind and the boat for apparent wind). Furthermore, for a problem involving wind velocities, it seems conceptually simpler to me to represent the boat (observer) velocities relative to the mass of air rather than to the ground. In this frame of reference (i.e., in the mass of air), the direction of the observer through the air mass is the negative of the direction of the air past the observer, i.e. of the wind direction.
The vector diagram presented below represents the various quantities of interest. In this diagram, TW denotes the true wind velocity (relative to the ground), B denotes the boat velocity (relative to the ground, measured by GPS) and AW denotes the apparent wind speed velocity (relative to the boat/observer). I have oriented the frame of reference (air mass) so that the observer (on the boat) is facing directly into the wind, headed along the y axis (i.e., “up” the page). (Remember that this diagram is in terms of boat velocities relative to the air mass. The wind vectors pictured in the US Sailing diagrams are the negatives of these velocities, and the vectors in their diagrams do not “add.”)
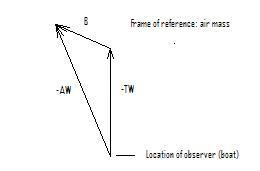
The problem with the diagram shown is that it does not (in general) involve right angles, and so the calculation of the quantities of interest is complicated. The calculations are simplified by rotating the diagram so that it is (always) included in a right triangle. Let us assume, as was done in the US Sailing example, that the boat velocity vector is oriented “up.” Then we have the following vector diagram. Since a right triangle is involved, calculation of the relationships is straightforward. A principal advantage of this particular orientation is that it displays the directions (angles off the bow) of the true and apparent winds to the boat in a very natural fashion. The direction (angle off the bow) of the true wind to the boat is denoted by dTW and the direction (angle off the bow) of the apparent wind to the boat is denoted by dAW. (The angle of the wind (either apparent or real) off the bow is measured clockwise in degrees from the pointing direction of the boat. For example, a headwind is zero degrees and a wind coming directly from the right (starboard) is ninety degrees.)
Notation. AW refers to a vector (velocity) whose magnitude (speed) is AWS and direction (“angle”) is dAW. TW refers to a vector whose magnitude is TWS and direction is dTW. B refers to a vector whose magnitude is BS and direction is zero degrees off the bow.
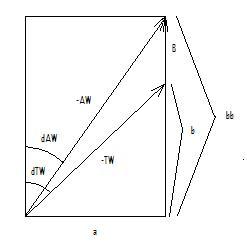
The formulas for the true wind speed (TWS) and direction (dTW), given the apparent wind speed (AWS) and direction (dAW) and the boat speed (BS) are:
Y = 90 – dAW
a = AWS cos Y
bb = AWS sin Y
b = bb – BS
TWS = (a2 + b2)1/2
dTW = 90 – arctan (b/a)
The formulas for the apparent wind speed (AWS) and direction (dAW), given the true wind speed (TWS) and direction (dTW) and the boat speed (BS) are:
Y = 90 – dTW
a = TWS cos Y
bb = TWS sin Y
bb = b + BS
AWS = (a2 + b2)1/2
dAW = 90 – arctan (bb/a)
Here are some sample calculations:
True wind speed = 8 knots
True wind direction = 0 degrees off the bow
Boat speed = 6 knots
Apparent wind speed = 14 knots
Apparent wind direction = 0
Apparent wind speed = 13 knots
Apparent wind direction = 20 degrees off the bow
Boat speed = 6 knots
True wind speed = 7.14 knots
True wind direction = 35.58 degrees off the bow
Here are some examples of the Raymarine output (actual screen output while sailing):
Ground wind speed: 8 (knots)
True wind speed: 14
Apparent wind speed: 14
Speed over ground: 6
Wind angle = 0 (degrees)
Ground wind speed: 7
True wind speed: 13
Apparent wind speed: 13
Speed over ground: 6
Wind angle: 20
Ground wind speed: 6
True wind speed: 10
Apparent wind speed: 10
Speed over ground: 6
Wind angle: 45
Ground wind speed: 9
True wind speed: 15
Apparent wind speed: 15
Speed over ground: 7
Wind angle: 0
Ground wind speed: 8
True wind speed: 14
Apparent wind speed: 14
Speed over ground: 7
Wind angle: 0
The Raymarine output appears to be correct if “ground wind” is true wind speed and “speed over ground” is boat speed. If so, what does Raymarine mean by “true wind”?
Special Case
Note that if the value of a in the formulas presented above is zero, the term b/a is undefined (“infinite”). This corresponds to the case in which the boat is headed directly into the wind. In this case, the formulas fail. In these cases, the apparent wind is simply the sum of the true wind and the boat speed. The US Sailing wind speed calculator handles this case, but the Starpath wind speed calculator does not – it returns the value NaN (“Not a Number”) as the result (speed).
True Wind Direction Relative to Ground (Geographic North or Magnetic North)
The formulas presented above give the true wind direction relative to the boat, i.e., degrees off the bow. What is more useful to record and report is the true wind direction relative to the ground, i.e., relative to geographic north (or perhaps to magnetic north, as reported by a compass). If the boat direction is north, then the true wind direction relative to north (that is, blowing from the north) is the same as the direction off the bow (i.e., angle off the bow). If the boat is headed in a direction dC degrees east of north, and the true wind direction is dTW degrees off the bow (clockwise), then the true wind direction relative to north (i.e., coming from the north) is dTW + dC. For example, if the boat is headed due north and the true wind direction is 15 degrees off the bow, then the true wind direction relative to north is 15 degrees east of north (i.e., the wind is blowing from a direction 15 degrees east of north). Or, if the boat is headed 10 degrees east (of north), and the true wind direction is 15 degrees (clockwise) off the bow, then the true wind direction relative to north is 25 degrees east of north.
FndID(124)
FndTitle(Miscellany51: Apparent Wind Speed and True Wind Speed)
FndDescription(Miscellany51: Apparent Wind Speed and True Wind Speed)
FndKeywords(apparent wind speed; true wind speed; wind speed)