Determination of Sample Size for Analytical Surveys, Using a Pretest-Posttest-Comparison-Group Design
Joseph George Caldwell, PhD (Statistics)
1432 N Camino Mateo, Tucson, AZ 85745 USA
Tel. (001)(520)222-3446, E-mail jcaldwell9@yahoo.com
Updated November 11, 2016
Minor edit September 1, 2020
Copyright © 2011-2016 Joseph George Caldwell. All rights reserved. Posted at Internet web site http://www.foundationwebsite.org. May be copied or reposted for non-commercial use, with attribution to author and website.
Introduction. The following article presents an example of sample size determination for an evaluation of a hypothetical agricultural development program. The basic evaluation design is a four-group, pretest-posttest-comparison-group design, implemented using a stratified two-stage sample survey design in which a stratified first-stage sample of districts is selected followed by a second-stage sample of households within each selected district. The districts are stratified (using marginal stratification with variable probabilities of selection) by district-level variables (available from a geographic-information-system (GIS) database) that affect agricultural output, such as elevation, temperature, and precipitation. The primary motivation for the stratification is to assure variation in variables that are expected to affect agricultural productivity (to enhance the precision of regression models in the data analysis).
Places in which the article should be modified to accommodate other sample designs are indicated (with notes placed in square brackets).
The basic design involves randomized assignment of districts to treatment, not households to treatment. The reason for this is that the program is implemented at the district level, but the selection of farmers for participation is determined by recruitment and screening, not by random assignment. (Because of the non-randomized assignment of farmers to treatment, the analysis to estimate program impact would require the use of causal-analysis models (such as a Neyman-Rubin Causal Model or a Heckman Causal Model) to account for selection effects.)
For descriptive surveys, the standard approach to sample size estimation is to estimate the precision of estimates of interest corresponding to a specified sample size and survey design, or to estimate the sample size required (or sample sizes required at each level of sampling, if multistage sampling is used) to achieve a specified level of precision. For analytical surveys, the standard approach to sample size estimation is to estimate the sample size required (or sample sizes required at each level of sampling, if multistage sampling is used) to achieve a specified power (probability) of detecting an impact of specified size, using a specified test. For this project, we will employ the latter method. The size of impact to be detected is called the minimum detectable effect, or minimum detectable impact.
In order to estimate sample size, the following must be specified (in order to estimate power):
1. The impact estimator to be used
2. The test parameters (power level, significance level)
3. The minimum detectable effect
4. Characteristics of the sampled (target) population (means, standard deviations, intra-unit correlation coefficients (if multistage sampling is used))
5. The sample design to be used for the sample survey to collect quantitative data
The Impact Estimator
The power calculations presented below will be made for a estimating the double difference in means for pretest-posttest-comparison-group design. For a design based on randomized assignment to treatment (i.e., an “experimental design”), an unbiased estimator of the average treatment effect (ATE) is the “double-difference” estimator (i.e., the difference, between the treatment and control samples, of the difference in means between the before and after samples). If randomized assignment is not used, the “raw” double difference estimator is biased, and it is necessary to use regression analysis to obtain an unbiased estimate of the ATE. For a regression model based on this design, the estimate of the average treatment effect is the coefficient of the treatment indicator variable. This coefficient is the double-difference estimator if no explanatory variables are included in the model. When explanatory variables are included, the regression equation (coefficient) estimates ATE(x), where x denotes the vector of explanatory variables, and the estimate of ATE is obtained by averaging ATE(x) over the values of x.)
The Test Parameters
The power analysis assumes that a one-sided test is being made of the hypothesis that the impact effect exceeds the value D, which is the minimum detectable effect. A one-sided test is used because in evaluation projects it is generally known in which direction change will occur. The test parameters are the probability, α, of making a Type I error of deciding that the effect exceeds D when in fact it does not, and the probability, β, of making a Type II error of deciding that the effect does not exceed D when it in fact does. The parameter α is called the size (or significance level) of the test, and the parameter 1 – β, which is the probability of correctly deciding that the effect exceeds D when it in fact does, is called the power of the test. We shall assume the values α = .05 and β = .1 (i.e., a power of 90%).
The Minimum Detectable Effect
The minimum detectable effect, D, is the smallest effect size, measured as a double difference, that is to be detected with power 1 – β (here assumed to be 90%). The value of D may differ for different outcome variables of interest. The value of D may be specified by program staff (e.g., in a monitoring and evaluation plan), or, alternatively, the power analysis may be done by specifying a range of values for D and estimating the power in each case. The calculations are done for a range of sample sizes, and a sample size is selected that satisfies budgetary constraints and has a high probability (power) of detecting effects of anticipated magnitudes.
Characteristics of the Sampled Population
In order to determine power, it is necessary to specify the means and standard deviations of the outcome variables of interest. (If two-stage sampling is done, it is also necessary to specify the intra-unit correlation coefficient (icc) of the first-stage sampling units, or primary sample units (PSUs). The icc may differ for each outcome variable.) This information may be available from previous sample surveys, or obtained by analysis of existing data bases. If not, assumptions are made about population means and standard deviations, and power calculations are made conditional on those assumptions.
For outcome variables that are proportions, the situation is simplified, since the standard error of an estimated proportion is a function of the true value of the proportion. If the true value of the proportion is p, then the standard deviation is sqrt(p(1-p)). The value of p for which the standard deviation is maximum is p = .5. For this value, the standard deviation is also .5. The power calculations presented below assume these values for the mean and the standard deviation. If it is desired to specify other values for the mean and standard deviation, then the power calculations can be redone.
If the minimum detectable effect, D, is specified in standard-deviation units, it is not necessary to specify the population standard deviation, σ, but only the relative standard error, σ/μ (i.e., the coefficient of variation). This is sometimes helpful in specifying the population characteristics needed for the power formula, since in many applications the coefficient of variation is known, whereas the standard deviation is not. For example, in many developing countries the coefficient of variation of income in rural areas varies from .5 to 2, and the value 1 may be used as a nominal value.
Estimates of sample sizes will now be presented, based on assumptions about the preceding items, and the assumption that the impact estimator is the double-difference estimator. The formula on which power calculations are based is the following. This formula shows the sample size, n, as a function of β (i.e., 1 – power). In order to show β as a function of n, simply solve the following formula for β:
n = (zα + zβ)2 var / D2
where
n = sample size
D = minimum detectable effect
zα = standard normal deviate having probability α to the right, where α denotes the significance level of the one-sided test of hypothesis that D exceeds zero (i.e., the probability of making a Type I error of deciding that D exceeds zero when in fact it does not)
zβ = standard normal deviate having probability β to the right, where 1 – β denotes the power of the test (i.e., the probability of deciding that D exceeds zero when it does). (β denotes the probability of making a Type II error of deciding that D does not exceed zero when in fact it does.)
var = variance factor for impact estimator.
The value of var is given by
var = deff [σ12 + σ22 + σ32 + σ42 -2ρ12σ1σ2 – 2 ρ13σ1σ3 + 2ρ14σ1σ4 + 2ρ23σ2σ3 - 2ρ24σ2σ4 - 2ρ34σ3σ4]
where
the four design groups are designated by the indices 1 (treatment before), 2 (treatment after), 3 (comparison before) and 4 (comparison after)
σi2 = variance for group i
ρij = coefficient of correlation between groups i and j
deff = Kish’s design effect (to reflect the effect of survey design features such as stratification and multi-stage sampling) (deff is the ratio of the variance of the estimator under the design to the variance using a simple random sample of the same size).
The factor deff is a variance adjustment factor that takes into account all of the features of the design and the analysis which modify the variance from the quantity included in brackets. This includes the effect of multistage sampling (or "clustering"), the effect of stratification, and the effect of regression models used in the analysis (after the questionnaire data are available). In fact, the effect of all of these factors are combined in the analysis, which would take all of them into account in a single estimation procedure. Conceptually, although it is an oversimplification, it is helpful to consider them separately in constructing sample size estimates. From this perspective, we may write
deff = deffclustering deffstratification deffregressionanalysis,
where deffclustering represents the variance adjustment caused by multistage sampling ("clustering"), deffstratification represents the variance adjustment caused by stratification, and deffregressionanalysis represents the variance adjustment caused by regression analysis (simple covariate adjustment or causal modelling). The effects of matching are accounted for by the term in brackets. (It is emphasized that this is a conceptual model, and that in fact all design features contribute to variance adjustment in a combined fashion in the data analysis, not strictly in the multiplicative fashion shown. Since the three design features mentioned – multistage sampling, stratification, and regression analysis may in fact be applied independently, this conceptual model is not unreasonable. The deffstratification factor may be considered to be the additional adjustment (to the variance of the double-difference estimator) of stratification after taking into account the effect of clustering, and the deffregressionanalysis factor may be considered to be the additional adjustment (to the variance) of regression analysis after all other factors have been taken into account.)
The effect of multistage sampling is usually to increase the variance rather substantially, e.g., by a factor of two or more. Multistage sampling is used even though it generally increases the variance over that obtained using simple random sampling (for the same total element sample size) because it is generally more efficient (i.e., provides a higher level of precision or power for a specified survey cost).
Stratification may increase or decrease the variance. If stratification is used to assure adequate sample sizes for subpopulations of special interest, it may increase the variance substantially (if the allocation of the sample departs substantially from proportional to population). If stratification is used specifically to increase precision (by allocation the sample in a way that takes into account both sampling costs and stratum variances, e.g., the Neyman allocation), then precision may be increased substantially. In the present application, stratification is being used at the district level mainly to assure adequate variation in variables that may have a significant effect on outcomes of interest. It may increase the precision of some regression-model parameter estimates, and decrease the precision of some overall-population estimates, such as means, proportions and totals.
Note that the preceding formula assumes sampling from an infinite population. In evaluation research, the objective is to make inferences about the effect of a program intervention on a population. It is not, as is the case for descriptive surveys, to make inferences about overall characteristics (means, proportions, totals) of the particular finite population at hand. For this reason, the “finite population correction” does not appear in the preceding formula.
The Sample Design
As mentioned, the power formula presented above corresponds to a double-difference estimator based on a pretest-posttest-comparison-group (or “four-group”) design. In an analytical design, the major design features to consider typically involve matching to increase precision of differences and regression coefficients (which are similar to differences). The present project will involve two types of matching [MODIFY this assertion, as appropriate]. First is matching of individual households in the two survey rounds (pretest/posttest), implemented by interviewing the same household in both survey rounds. Second is matching of treatment and comparison districts on design variables that are considered to have an appreciable effect on outcomes of interest.
Apart from matching, the other major design features that affect precision and power are multistage sampling and stratification.
The effects of the preceding design features will be reflected in design-effect parameters in the formula used to estimate power. The effect of interviewing the same households in both panels will be indicated by a “panel” correlation (i.e., the coefficient of correlation between observations made on the same household in the two survey rounds). This correlation may differ for different outcome variables. [MODIFY the following assumptions, as appropriate.] For the present application, it is expected to be fairly high for most variables, such as ρ12 = ρ34 =.5. The effect of matching of treatment and comparison districts is expected to be modest, e.g., a correlation coefficient of.1-.2. We shall assume the value ρ13 = ρ24 = .1. (The values of ρ14 and ρ23 are "artifactual" (not physically meaningful), and we specify them as ρ14 = ρ12 ρ13 = (.5) (.1) = .05 and ρ23 = ρ24 ρ34 = (.5) (.1) = .05. The rationale for these values is presented in the sample-size estimation program, SampleSize.exe.)
Since two-stage sampling is involved in this design, it is necessary to specify sample sizes for both the first-stage and second stage units. We propose selecting a fixed number of second-stage units (households) from each selected first-stage unit (district, primary sampling unit (PSU), and to select the first-stage units within design strata with probabilities proportional to size (number of households). To determine the optimal number, m, of households to select from each district, it is necessary to take into account the relative costs of sampling first- and second-stage units, and the intra-unit correlation, ρ. As mentioned, the value of ρ may be different for each outcome variable of interest.
If the within-unit (within-district) sample size is a constant, m, as is assumed here, then the variance of the sample mean is given (approximately) by
![]() .
.
The factor (1 + (m-1)ρ) is hence the design effect, deffclustering, associated with multistage sampling.
For many applications, ρ is in the range .05 - .15, and m is in the range 10-20. For ρ = .05 and m = 10, the value of deffclustering is 1.45. For ρ = .10 and m = 15, deffclustering = 2.4. For ρ = .15 and m = 20, deffclustering = 3.85. Typical “nominal” values for ρ and m are ρ = .1 and m = 12, for which deffclustering = 2.1.
Since the value of ρ varies according to the variable being measured, it is useful in the detailed sample design effort to estimate sample sizes for several values of ρ, including values in the range expected for the most important outcome variables. For the initial estimation of sample size, a typical ("nominal") value may be used.
An optimal value for m may be determined by specifying the ratio of the costs of sampling first-stage and second-stage sample units, and the ratio of the variances of the first- and second-stage units. The value of m is determined by minimizing the variance of the estimate given total cost, or minimizing the total cost given the variance. The optimal value of m does not depend on n.
[Optional section, on determining an optimal value of m.]
Determination of the optimal value of m would likely not be done for a preliminary estimation of sample size, but in the detailed survey design (which is not addressed here). The formula for the optimal value of m, denoted by mopt, is as follows.
Suppose that the cost of sampling is given by the function
C = c1n + c2nm
where c1 denotes the marginal cost of sampling a first-stage unit and c2 denotes the marginal cost of sampling a second-stage unit.
Then

where M denotes the size of the first-stage units. If the denominator is zero or negative, then all subunits are selected (i.e., one-stage sampling is used). This may be expressed as
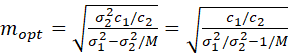 .
.
If we define σu2 = σ12 – σ22/M, mopt may be written as
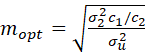 .
.
Since σ22/σu2 is approximately equal to (1 – ρ)/ρ (where ρ denotes the intra-unit correlation), this expression is approximately
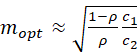 .
.
If something is known about the value of σ22/σ12, σ22/σu2 or the value of ρ, then mopt may be estimated (as a function of c1/c2). In most applications the optimum is rather flat, so that an error in mopt does not affect precision very much. The value ρ = .5 ( a high value) corresponds to σ22/σu2 = 1; ρ = .1 ( a moderate value) corresponds to σ22/σu2 = 9; ρ = .01 ( a low value) corresponds to σ22/σu2 = 99.
In international development applications, for two-stage sampling where the first-stage sample unit is a village and the second-stage unit is a household, the value of m is generally set according to how many household interviews the field survey team can conduct in a village in a single day or two days. A typical value for m in this setting is 12. If ρ = .1 and c1/c2 = 30, then mopt = sqrt(30(1 - .1)/.1) = 16.
[End of optional section, on determining an optimal value of m.]
For the present, we shall assume "nominal" values of ρ=.1 and m=12, in which case deffclustering = (1 + (m-1)ρ) = (1 + (12-1).1 = 2.1.
The preceding discussion has addressed the effects of the design feature of two-stage sampling on precision (and hence on power). In addition to two-stage sampling (and, of course, matching), the other salient feature of the design is stratification.
In this application, stratification is used to achieve variation in explanatory variables in regression models to be used in the data analysis, rather than to achieve an "optimal" allocation to increase the precision of estimates of population means, proportions or totals. That is, it is used here to increase the precision of "model-based" estimates such as regression-model coefficients, not of overall-population "design-based" estimates such as estimates of means, proportions and totals. This sort of stratification may reduce precision of estimates of population means, proportions and totals to the extent that it "unbalances" the allocation of the sample to strata from proportional allocation. At the present time, little is known about either of these effects (more will be learned in the construction of a detailed sample design). The effect of stratification on precision (and hence on power) is expected to be modest, compared to the effects of multistage sampling and matching. (This assessment applies to either design-based (double difference) or model-based (regression-model) estimates of impact, since both essentially involve differences among treatment-comparison groups and survey rounds, and the precision of these estimates is determined mainly by the design matching.) The primary purpose of using regression analysis in this application will be to reduce bias associated with selection effects, not to increase precision (or power) by consideration of covariates that affect outcome. For these several reasons, we shall assume that the effects of stratification and regression analysis, compared to the effect of matching and multistage sampling, are low, and set the values of deffstratification and deffregressionanalysis equal to 1.0.
The combined design effect of multistage sampling and stratification is taken to be the product of deffclustering, deffstratification and deffregressionanalysis, or deff = deffclustering deffstratification deffregressionanalysis = 2.1 x 1.0 x 1.0 = 2.1.
Statistical Power Analysis (Estimation of Sample Size)
The following table presents the power function corresponding to the assumptions specified above, for a range of sample sizes. (These sample-size calculations were done using the program SampleSize.exe, module 6d, setting α = .05, deff = 2.1, and sample sizes ranging from 500 to 4,000 in increments of 500.) The “power function” is the power for a range of values of the minimum detectable effect, D, measured as a double difference of proportions. D is varied from zero to .3. In the table, the specified sample size is for each of the four design groups. For example, a sample size of 1,000 corresponds to 1,000 treatment before, 1,000, comparison before, 1,000 treatment after, and 1,000 comparison after, for a total sample size (treatment and comparison groups over two survey rounds) of 4,000. The sample size specified in the table is the number of households. For the sample size in terms of districts, divide the tabled sample size by 12 (since 12 households are selected from each sample district). (For example, a sample size of 1,000 households corresponds to a district sample size of 1,000/12 = 83. For the actual sample design, the household sample size will be a multiple of the within-district household sample size, m = 12, e.g., 84 x 12 = 1,008, not 1,000.)
|
Power Function Corresponding to Different Sample Sizes (α=.05, deff=2.1) Table entry is the power (probability of detecting an effect of size D) |
|||||
|
Sample Size of Each Design Group |
Minimum Detectable Effect, D (for a proportion with baseline value p=.5) |
||||
|
0 |
.05 |
.1 |
.2 |
.3 |
|
|
500 |
.05 |
.311 |
.744 |
.997 |
1.0 |
|
1000 |
.05 |
.493 |
.945 |
1.0 |
1.0 |
|
1500 |
.05 |
.636 |
.990 |
1.0 |
1.0 |
|
2000 |
.05 |
.744 |
.997 |
1.0 |
1.0 |
|
2500 |
.05 |
.822 |
.335 |
1.0 |
1.0 |
|
3000 |
.05 |
.878 |
1.0 |
1.0 |
1.0 |
|
3500 |
.05 |
.916 |
1.0 |
1.0 |
1.0 |
|
4000 |
.05 |
.995 |
1.0 |
1.0 |
1.0 |
This table shows that a sample size of 1,000 can detect, for example, a double-difference change of D=.1 in a proportion with high probability (.945). If analysis is done using a small portion of the sample, e.g., 500 observations, then the probability of detecting such an effect size is .744.
File name: SampleSizeEstimationAnalyticalSurveysGeneric.doc
FndID(180)
FndTitle(Determination of Sample Size for Analytical Surveys, Using a Pretest-Posttest-Comparison-Group Design)
FndDescription(The following article presents an example of sample size determination for an evaluation of a hypothetical agricultural development program. The basic evaluation design is a four-group, pretest-posttest-comparison-group design.)
FndKeywords(sample size estimation; sample size determination; statistical precision analysis; statistical power analysis; pretest-posttest-comparison-group; two-sstage sample design)