CONTINUOUS MULTIVARIATE ANALYSIS: LECTURE NOTES
Joseph George Caldwell, PhD (Statistics)
1432 N Camino Mateo, Tucson, AZ 85745-3311 USA
Tel. (001)(520)222-3446, E-mail jcaldwell9@yahoo.com
Version without figures
March 21, 2018
Copyright © 2018 Joseph George Caldwell. All rights reserved.
Contents
2. CLASSIFICATION OF THE PROBLEMS OF MULTIVARIATE ANALYSIS. 4
3. VECTOR AND MATRIX ALGEBRA RELATED TO CONTINUOUS MULTIVARIATE ANALYSIS. 6
4. SOME PARTICULAR MULTIVARIATE DISTRIBUTIONS. 26
5. MULTIVARIATE TECHNIQUES WHEN THE POPULATION PARAMETERS ARE KNOWN.. 31
MARGINAL AND CONDITIONAL DISTRIBUTIONS; DISTRIBUTION OF LINEAR COMBINATIONS. 32
REGRESSION AND CORRELATION.. 32
MULTIPLE CORRELATION COEFFICIENT. 34
THE GENERAL LINEAR STATISTICAL MODEL. 34
CANONICAL CORRELATIONS AND CANONICAL VARIABLES. 38
6. ESTIMATION AND HYPOTHESIS TESTING.. 47
ESTIMATION OF THE MEAN VECTOR AND COVARIANCE MATRIX. 47
TESTS OF HYPOTHESES ABOUT ONE OR TWO MEAN VECTORS. 50
TESTS OF HYPOTHESES ABOUT COVARIANCE MATRICES. 52
THE MULTIVARIATE GENERAL LINEAR STATISTICAL MODEL. 52
MULTIVARIATE ANALYSIS OF VARIANCE AND ANALYSIS OF COVARIANCE. 56
PRINCIPAL COMPONENTS ANALYSIS. 57
MULTIVARIATE TIME SERIES MODELS (SUMMARY) 61
1. OVERVIEW
THIS PRESENTATION SUMMARIZES THE THEORY OF MULTIVARIATE STATISTICAL ANALYSIS FOR CONTINUOUS RANDOM VARIABLES. THE PRESENTATION INCLUDES A SUMMARY DESCRIPTION OF THE MAJOR TOPICS OF THIS FIELD. A BRIEF DESCRIPTION OF MULTIVARIATE ANALYSIS FOR DISCRETE RANDOM VARIABLES IS INCLUDED IN ANOTHER PRESENTATION (ON STATISTICAL INFERENCE).
A MAJOR FOCUS OF THE PRESENTATION IS TO COVER MATERIAL THAT IS NECESSARY TO AN UNDERSTANDING OF MULTIVARIATE TIME SERIES ANALYSIS.
CONTINUOUS MULTIVARIATE ANALYSIS REQUIRES A BASIC KNOWLEDGE OF VECTOR AND MATRIX OPERATIONS, SOME OF WHICH HAS BEEN INCLUDED IN OTHER PRESENTATIONS. THIS PRESENTATION SUMMARIZES THAT MATERIAL, AND THEN BUILDS ON IT.
THE TOPICS COVERED IN THIS PRESENTATION ARE THE FOLLOWING:
CLASSIFICATION OF MULTIVARIATE ANALYSIS METHODOLOGIES
VECTOR AND MATRIX ALGEBRA RELATED TO CONTINUOUS MULTIVARIATE ANALYSIS
SOLUTION OF EQUATIONS
THE GENERAL LINEAR STATISTICAL MODEL
THE GENERALIZED LINEAR STATISTICAL MODEL
OPTIMIZATION AND CONSTRAINED OPTIMIZATION
SOME MULTIVARIATE DISTRIBUTIONS
THE MULTIVARIATE GENERAL LINEAR MODEL
MULTIVARIATE ANALYSIS OF VARIANCE AND ANALYSIS OF COVARIANCE
PRINCIPAL COMPONENTS ANALYSIS
FACTOR ANALYSIS
CANONICAL CORRELATION
DISCRIMINANT ANALYSIS
CLASSIFICATION ANALYSIS
MULTIVARIATE TIME SERIES MODELS (SUMMARY)
THERE ARE A LARGE NUMBER OF TEXTBOOKS COVERING THE SUBJECT OF MULTIVARIATE ANALYSIS. A SELECTION OF THESE BOOKS IS THE FOLLOWING:
Fienberg, Stephen E., The Analysis of Cross-Classified Categorical Data, The MIT Press, 1977
Agresti, Alan, An Introduction to Categorical Data Analysis, Wiley, 1996
Agresti, Alan, Categorical Data Analysis, Wiley, 1990
Anderson, T. W., An Introduction to Multivariate Statistical Analysis, Wiley, 1958
Roy, S. N., Some Aspects of Multivariate Analysis, Asia Publishing House, 1958
Lawley, D. N., and A. E. Maxwell, Factor Analysis as a Statistical Method, Butterworths, 1963
Harman, Harry H., Modern Factor Analysis 2nd ed. revised, University of Chicago Press, 1960
Cooley, William W. and Paul R. Lohnes, Multivariate Data Analysis, Wiley, 1971
Berridge, Damon M. and Robert Crouchley, Multivariate Generalized Linear Mixed Models Using R, CRC Press / Chapman & Hall, 2011
MANY BOOKS CONTAIN SECTIONS DEALING WITH MULTIVARIATE APPLICATIONS WITHIN A LARGER SUBJECT AREA, SUCH AS:
Rao, C. Radhakrishna Rao, Linear Statistical Inference and Its Applications, 2nd ed., Wiley, 1965, 1973
McCulloch, Charles E., Shayne R. Searle, and John M. Neuhaus, Generalized, Linear and Mixed Models, 2nd ed., Wiley, 2008
MANY BOOKS INCLUDE APPENDICES THAT PRESENT SUMMARY DESCRIPTIONS OF MULTIVARIATE ANALYSIS AND RELATED VECTOR AND MATRIX ALGEBRA. THESE INCLUDE:
Tsay, Ruey S., Multivariate Time Series Analysis with R and Financial Applications, Wiley, 2014
Lϋtkepohl, Helmut, New Introduction of Multiple Time Series Analysis, Springer, 2006
Hamilton, James D., Time Series Analysis, Princeton University Press, 1994
Greene, William H., Econometric Analysis 7th ed., Prentice Hall, 2012
2. CLASSIFICATION OF THE PROBLEMS OF MULTIVARIATE ANALYSIS
FIENBERG (OP. CIT.) PROVIDES A SUCCINCT CLASSIFICATION OF THE MAJOR CATEGORIES OF MULTIVARIATE ANALYSIS, CLASSIFIED BY WHETHER THE EXPLAINED AND EXPLANATORY VARIABLES OF AN APPLICATION ARE CONTINUOUS, DISCRETE, OR BOTH.
|
Explanatory Variables |
||||
|
Categorical |
Continuous |
Mixed |
||
|
Response Variables |
Categorical |
a |
b |
c |
|
Continuous |
d |
e |
f |
|
|
Mixed |
g |
h |
i |
|
APPLICATIONS IN CATEGORY a ARE CROSS-CLASSIFIED CATEGORICAL DATA PROBLEMS (MULTIDIMENSIONAL CONTINGENCY TABLES), AND ARE DEALT WITH IN TEXTS SUCH AS FIENBERG AND AGRESTI (OP. CIT.). AN EXAMPLE OF THIS TYPE OF APPLICATION IS THE LOG-LINEAR MODEL, WHICH IS DISCUSSED IN A SEPARATE PRESENTATION (ON STATISTICAL INFERENCE). FOR APPLICATIONS INVOLVING A SINGLE RESPONSE VARIABLE, THOSE IN CATEGORIES b AND c ARE DEALT WITH USING GENERALIZED LINEAR MODELS (SUCH AS LOGISTIC AND PROBIT MODELS).
APPLICATIONS IN THE MIDDLE ROW OF THE TABLE (d, e, AND f) CORRESPOND TO THE STANDARD MODELS OF MULTIVARIATE ANALYSIS, INCLUDING MULTIVARIATE ANALYSIS OF VARIANCE (d), MULTIVARIATE REGRESSION ANALYSIS (e), AND MULTIVARIATE ANALYSIS OF COVARIANCE (OR REGRESSION ANALYSIS WITH CATEGORICAL (“DUMMY”) EXPLANATORY VARIABLES (f).
APPLICATIONS IN THE LAST ROW OF THE TABLE ARE HANDLED BY MEANS OF SPECIALIZED MODELS. EXAMPLES OF TECHNIQUES FOR ANALYZING SUCH PROBLEMS ARE PRESENTED IN BERRIDGE AND CROUCHLY (OP. CIT.).
THIS PRESENTATION DEALS MAINLY WITH APPLICATIONS OF TYPE e (I.E., MULTIVARIATE PROBLEMS IN WHICH ALL VARIABLES ARE CONTINUOUS, WHETHER EXPLANATORY OR EXPLAINED).
A COMMENT ON TERMINOLOGY. CONFUSION OFTEN ARISES INVOLVING THE MEANING OF THE TERM “MULTIVARIATE.” AN APPLICATION IS A MULTIVARIATE APPLICATION ONLY IF IT INVOLVES A JOINT DISTRIBUTION OF RANDOM VARIABLES THAT MAY NOT BE INDEPENDENT. AN APPLICATION MAY INVOLVE MULTIPLE VARIABLES, EITHER RANDOM OR DETERMINISTIC, AND NOT BE A MULTIVARIATE APPLICATION. FOR EXAMPLE, A REGRESSION ANALYSIS INVOLVING A SINGLE RESPONSE VARIABLE AND A NUMBER OF EXPLANATORY VARIABLES (EITHER RANDOM OR DETERMINISTIC) IS A “MULTIVARIABLE” PROBLEM, BUT IT IS NOT A MULTIVARIATE PROBLEM – IT IS A UNIVARIATE PROBLEM.
3. VECTOR AND MATRIX ALGEBRA RELATED TO CONTINUOUS MULTIVARIATE ANALYSIS
THE SUBJECT OF VECTOR AND MATRIX ALGEBRA IS COVERED IN A COURSE IN LINEAR ALGEBRA. THIS SECTION WILL DESCRIBE CONCEPTS OF VECTOR AND MATRIX ALGEBRA SUFFICIENT TO ENABLE AN UNDERSTANDING OF THE BASIC CONCEPTS OF CONTINUOUS MULTIVARIATE ANALYSIS.
REFERENCE TEXTS ON VECTORS AND MATRICES INCLUDE THE FOLLOWING:
Perlis, Sam, Theory of Matrices, Addison-Wesley, 1952 (reprinted by Dover, 1991)
Hadley, G, Linear Algebra, Addison-Wesley, 1961
Schneider, Hans and George Phillip Barker, Matrices and Linear Algebra, 2nd ed. Holt, Reinhart and Winston, 1968 (Dover edition 1989)
Searle, S. R. and W. H. Hausman, Matrix Algebra for Business and Economics, Wiley, 1970
Graybill, Franklin A., Introduction to Matrices with Applications in Statistics, Wadsworth, 1969
THE PRECEDING TEXTS ARE COMPREHENSIVE AND DETAILED. FOR THE PURPOSES OF THIS PRESENTATION, THEY INCLUDE MUCH MORE INFORMATION THAN IS NEEDED.THE MATERIAL PRESENTED IN THE APPENDICES LISTED EARLIER ON MULTIVARIATE ANALYSIS IS SUFFICIENT (I.E., TO TSAY, HAMILTON, LÜTKEPOHL, AND GREENE). THIS PRESENTATION IS SIMILAR TO BUT BRIEFER THAN THOSE SUMMARIES, PRESENTING THE MINIMAL AMOUNT OF THEORY REQUIRED FOR THIS PRESENTATION.
AS MENTIONED, SOME BASIC MATERIAL ON VECTORS AND MATRICES IS PRESENTED IN OTHER PRESENTATIONS OF THIS SERIES (IN PARTICULAR, DAY 10 ON SMALL-AREA ESTIMATION). IN THE INTEREST OF CONTINUITY AND COMPLETENESS OF THIS PRESENTATION, SOME OF THAT MATERIAL IS REPEATED HERE.
A COLUMN VECTOR IS A VERTICAL ARRAY OF A SEQUENCE OF n ELEMENTS
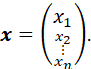
A ROW VECTOR IS A HORIZONTAL ARRAY OF A SEQUENCE OF n ELEMENTS
![]()
IN THIS APPLICATION, THE ELEMENTS ARE SYMBOLS OR VARIABLES OR NUMBERS.
VECTORS ARE INDICATED BY BOLDFACE OR UNDERLINED FONT. A VECTOR CONSISTING OF ONE ELEMENT IS CALLED A SCALAR. FOR EXAMPLE, x MAY DENOTE A SCALAR AND x AND x MAY DENOTE VECTORS.
THE ELEMENT xi IS CALLED THE i-th COMPONENT OF x. THE NUMBER OF COMPONENTS IN x IS VARIOUSLY CALLED THE DIMENSION OR SIZE OR LENGTH OF x. (THE TERMS “LENGTH” AND “SIZE” HAVE DIFFERENT MEANINGS, TO BE DEFINED LATER.)
THE TRANSPOSE OF A
COLUMN VECTOR x, DENOTED BY x’ or xT IS THE ROW
VECTOR OF LENGTH n, ![]() OR
OR ![]() . THE TRANSPOSE OF A ROW VECTOR IS DEFINED SIMILARLY.
. THE TRANSPOSE OF A ROW VECTOR IS DEFINED SIMILARLY.
THE TERM “VECTOR” MAY REFER TO EITHER A COLUMN VECTOR OR A ROW VECTOR. ABSENT AN EXPLICIT INDICATOR (PRIME OR “T”), AN ARBITRARY VECTOR IS ASSUMED TO BE A COLUMN VECTOR.
A MATRIX X OF m ROWS AND n COLUMNS (AN “m by n” MATRIX) IS A RECTANGULAR ARRAY OF ELEMENTS:
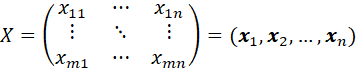
WE SHALL DENOTE MATRICES STANDARD (NON-BOLDFACE) FONT. (THIS IS NOT A UNIVERSAL CONVENTION – MOST AUTHORS WRITE VECTORS IN BOLDFACE, BUT MANY AUTHORS WRITE MATRICES IN BOLDFACE, ALSO.)
IF xij DENOTES THE ELEMENT IN ROW i AND COLUMN j OF MATRIX X, THEN THE MATRIX X MAY BE DENOTED AS X = [xij]. IF WE WISH TO MAKE THE NUMBER OF ROWS AND COLUMNS EXPLICIT, WE WRITE X = [xij]mxn. THE TRANSPOSE X’ (OR XT) IS DEFINED AS THE MATRIX HAVING ELEMENT xji IN ROW i AND COLUMN j. THE ROWS AND THE COLUMNS OF A MATRIX ARE VECTORS. A MATRIX HAVING JUST ONE ROW OR ONE COLUMN IS A VECTOR (OR, IF JUST ONE ROW AND ONE COLUMN, A SCALAR).
IF A MATRIX HAS THE SAME NUMBER OF ROWS AS COLUMNS, IT IS CALLED SQUARE, AND THE NUMBER OF ROWS (OR COLUMNS) IS CALLED THE SIZE OR ORDER OF THE MATRIX.
BASIC OPERATIONS ON MATRICES ARE THE FOLLOWING. SUPPOSE THAT A = [aij] IS AN m x n MATRIX AND B = [bij] IS A p x q MATRIX.
ADDITION: IF m=p AND n=q, THEN A + B = [aij + bij]mxn.
SUBTRACTION: IF m=p AND n=q, THEN A - B = [aij - bij]mxn.
SCALAR MULTIPLICATION: IF c IS A SCALAR, THEN cA = [caij].
MULTIPLICATION: AB = ![]() where n=p.
where n=p.
THE PRODUCT OF AN n BY m MATRIX A AND AN m BY k MATRIX B IS THE n BY k MATRIX WHOSE i,j-th ELEMENT (I.E., ENTRY IN ROW i AND COLUMN j) IS THE VECTOR PRODUCT OF THE i-th ROW OF A AND THE j-th COLUMN OF B. NOTE THAT THE PRODUCT IS DEFINED ONLY IF THE MATRICES ARE CONFORMABLE, I.E., THE NUMBER OF COLUMNS OF A IS EQUAL TO THE NUMBER OF ROWS OF B.
SINCE VECTORS ARE MATRICES, THE PRECEDING DEFINITIONS APPLY TO VECTORS. FOR EXAMPLE, THE PRODUCT OF A SCALAR a AND A VECTOR x WHOSE i-th COMPONENT IS xi IS THE VECTOR WHOSE i-th COMPONENT is axi: a x’ = (ax1, ax2,…,axn).
IF VECTORS a AND b
ARE OF THE SAME LENGTH n, THE VECTOR PRODUCT (OR INNER PRODUCT) IS ![]() . TWO VECTORS WHOSE INNER PRODUCT IS ZERO ARE SAID TO
BE ORTHOGONAL. (THIS DEFINITION REFERS TO GEOMETRIC ORTHOGONALITY; IN
STATISTICS, TWO RANDOM VECTORS ARE SAID TO BE ORTHOGONAL IF THEY ARE
UNCORRELATED.)
. TWO VECTORS WHOSE INNER PRODUCT IS ZERO ARE SAID TO
BE ORTHOGONAL. (THIS DEFINITION REFERS TO GEOMETRIC ORTHOGONALITY; IN
STATISTICS, TWO RANDOM VECTORS ARE SAID TO BE ORTHOGONAL IF THEY ARE
UNCORRELATED.)
THE DIAGONAL (OR MAIN DIAGONAL OR PRINCIPAL DIAGONAL) OF A MATRIX IS THE VECTOR OF ELEMENTS FOR WHICH THE ROW INDEX EQUALS THE COLUMN INDEX.
THE SQUARE MATRIX, I, SUCH THAT ALL OF THE DIAGONAL ELEMENTS EQUAL TO ONE AND ZEROS ELSEWHERE IS CALLED THE IDENTITY MATRIX, SINCE IA = A FOR ANY MATRIX A. (IF I IS AN n x n MATRIX, IT IS DENOTED AS In IF IT IS DESIRED TO INDICATE ITS SIZE.)
THE INVERSE OF A SQUARE MATRIX A IS A MATRIX B = A-1 SUCH THAT AB = I, IF IT EXISTS, IT IS UNIQUE, AND A-1 A = I. IF THE INVERSE EXISTS, THE MATRIX IS CALLED NONSINGULAR OR INVERTIBLE.
THE RANK, r, OF A MATRIX IS THE NUMBER OF LINEARLY INDEPENDENT ROWS OR COLUMNS (WHICH ARE EQUAL). FOR A SQUARE MATRIX, IF r=n, THE MATRIX IS SAID TO BE OF FULL RANK, AND IT IS INVERTIBLE.
A SYMMETRIC MATRIX IS A SQUARE MATRIX FOR WHICH xij = xji.
EXAMPLES:
THE MATRIX
![]()
IS OF RANK 2. ITS INVERSE IS THE SAME MATRIX.
THE MATRIX
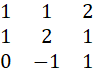
IS SINGULAR (NON-INVERTIBLE), SINCE THE THIRD ROW IS THE FIRST MINUS THE SECOND. IT IS OF RANK 2.
THE MATRIX
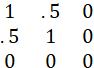
IS SINGULAR, AND OF RANK 2.
IN MATRIX NOTATION, A SYSTEM OF SIMULTANEOUS LINEAR EQUATIONS, FOR EXAMPLE,
y1 = a11 x1 + a12 x2
y2 = a21 x1 + a22 x2
MAY BE REPRESENTED AS
y = A x
WHERE y’ = (y1, y2), x’ = (x1, x2) AND A = (a1, a2) WHERE a1’ = (a11, a21) AND a2’ = (a12, a22).
CONSIDER THE SYSTEM OF LINEAR EQUATIONS
Ax = b
WHERE A IS AN n x n MATRIX AND x AND b ARE VECTORS OF LENGTH n. IT IS DESIRED TO DETERMINE NONZERO SOLUTIONS, x, TO THIS SYSTEM, WHICH ARE LINEAR COMBINATIONS OF THE COLUMNS OF A. THERE ARE TWO CASED TO CONSIDER, DEPENDING ON WHETHER b IS ZERO OR NONZERO. IF b IS ZERO, THE SYSTEM IS CALLED HOMOGENEOUS, AND IF b IS NONZERO THE SYSTEM IS CALLED NONHOMOGENEOUS.
IF b = 0, THEN A SOLUTION EXISTS IF AND ONLY IF THERE EXISTS A LINEAR COMBINATION (I.E., Ab) OF THE COLUMNS OF A THAT IS EQUAL TO 0. THAT IS, THERE IS A NONZERO SOLUTION TO THE SYSTEM IF AND ONLY IF A IS NOT OF FULL RANK, I.E., IS SINGULAR.
SUPPOSE THAT b IS NONZERO. IT IS DESIRED TO DETERMINE CONDITIONS UNDER WHICH THE SYSTEM HAS SOLUTIONS FOR ALL NONZERO VECTORS b, NOT JUST FOR SOME VECTORS b. IN THIS CASE, THERE IS A SOLUTION IF A IS INVERTIBLE, SINCE IN THAT CASE WE HAVE (PREMULTIPLYING BOTH SIDES OF THE SIMULTANEOUS EQUATIONS BY A-1),
A-1Ax = A-1b
OR
x = A-1b.
IF A IS NOT INVERTIBLE, THEN THERE IS NO MATRIX A-1 FOR WHICH A-1A = I, THAT IS, THERE IS NO MATRIX A-1 FOR WHICH A-1Ax = A-1b, I.E., NO MATRIX A-1 FOR WHICH x = A-1b. THAT IS, THERE IS NO LINEAR COMBINATION OF THE COLUMNS OF A WHICH SATISFY THE SYSTEM OF EQUATIONS.
IN SUMMARY, FOR b NOT EQUAL TO ZERO, THE SYSTEM HAS A NONZERO SOLUTION THAT MAY BE EXPRESSED AS A LINEAR COMBINATION OF THE COLUMNS OF A IF AND ONLY IF A IS NONSINGULAR. THE SOLUTION IS x = A-1b.
THE TRACE OF A MATRIX IS
THE SUM OF ITS DIAGONAL ELEMENTS: IF A IS AN nxn MATRIX, THEN ![]() . IT HOLDS THAT tr(A + C) = tr(A) + tr(C), tr(AC) =
tr(CA) AND tr(A) = tr(A’) (WHERE THE MATRICES ARE ASSUMED CONFORMABLE).
. IT HOLDS THAT tr(A + C) = tr(A) + tr(C), tr(AC) =
tr(CA) AND tr(A) = tr(A’) (WHERE THE MATRICES ARE ASSUMED CONFORMABLE).
SUPPOSE THAT A IS AN nxn
SQUARE MATRIX. A NUMBER λ AND AN nx1 NONZERO VECTOR b ARE A RIGHT
EIGENVALUE AND EIGENVECTOR PAIR OF A IF Ab=λb. THERE ARE UP TO n
POSSIBLE EIGENVALUES FOR A. THEY MAY BE COMPLEX NUMBERS, IN WHICH CASE THEY
OCCUR IN CONJUGATE PAIRS. DENOTE THE n EIGENVALUES AS λi FOR i=
1,…,n. THEN tr(A) = ![]() .
.
THE DETERMINANT OF A
MATRIX, A, DENOTED BY |A|, IS DEFINED AS ![]() . THE NOTATION det(A) IS ALSO COMMON FOR |A|.
. THE NOTATION det(A) IS ALSO COMMON FOR |A|.
IT CAN BE SHOWN THA T THE DETERMINANT OF A MATRIX A = [aij] MAY BE CALCULATED AS THE SUM OF ALL PRODUCTS
![]()
CONSISTING OF ONE ELEMENT FROM EACH ROW AND EACH COLUMN, WHERE p IS THE NUMBER OF INVERSIONS REQUIRED TO TRANSFORM THE PERMUTATION i1,…,im into 1,…,m. FOR EXAMPLE, FOR THE 2x2 MATRIX A = [aij], THE DETERMINANT IS a11a22 – a12a21.
SOME FEATURES OF DETERMINANTS ARE THE FOLLOWING, WHERE IT IS ASSUMED THAT ALL MATRICES ARE NONSINGULAR (INVERTIBLE):
1. IF A AND B ARE n x n MATRICES, THEN |AB| = |A||B|.
2. |A’| = |A|.
3. |A-1| = 1/|A|.
A MATRIX IS NONSINGULAR IF AND ONLY IF ALL OF ITS EIGENVALUES ARE NONZERO, I.E., ITS DETERMINANT IS NONZERO.
ALL OF THE EIGENVALUES OF A SYMMETRIC MATRIX ARE REAL.
THE RANK OF A MATRIX, A, IS THE NUMBER OF NONZERO EIGENVALUES OF THE SYMMETRIC MATRIX AA’.
SINCE THE EIGENVALUE / EIGENVECTOR PAIR λ, b SATISFY
Ab = λb,
IT FOLLOWS THAT
Ab – λIb = 0
OR
(A – λI)b = 0.
FROM THE DISCUSSION EARLIER ABOUT SOLUTIONS TO A SYSTEM OF SIMULTANEOUS EQUATIONS, THIS SYSTEM HAS A SOLUTION ONLY IF THE MATRIX A – ΛI IS SINGULAR.
IF (A – λI) WERE NONSINGULAR, THEN WE COULDPREMULTIPLY THE PRECEDING EXPRESSION BY (A – λI)-1 AND OBTAIN b = 0. BUT b IS ASSUMED TO BE NONZERO, HENCE (A – λI) MUST BE SINGULAR. HENCE AN EIGENVALUE OF A IS A NUMBER λ SUCH THAT |A – λI| = 0.
EIGENVALUES ARE ALSO CALLED CHARACTERISTIC VALUES OR CHARACTERISTIC ROOTS OR LATENT ROOTS, AND THE JUST-PRECEDING EQUATION IS CALLED THE CHARACTERISTIC EQUATION.
EIGENVECTORS SPAN THE VECTOR SPACE SPANNED BY THE ROWS OR COLUMNS OF A MATRIX. EIGENVALUES ARE MEASURES OF LENGTH ALONG EIGENVECTORS, AND THE DETERMINANT IS A MEASURE OF VOLUME. FOR EXAMPLE, CONSIDER THE CASE OF AN n x n IDENTITY MATRIX. THE EIGENVECTORS ARE UNIT VECTORS POINTING ALONG n ORTHOGONAL AXES. THE LENGTH OF EACH EIGENVECTOR IS ONE (THE CORRESPONDING EIGENVALUE), AND THE PRODUCT OF ALL OF THE LENGTHS (EIGENVALUES) IS THE n-DIMENSIONAL VOLUME OF THE n-DIMENSIONAL HYPERCUBE SPANNED BY THE n EIGENVECTORS.
THERE ARE A NUMBER OF NUMERICAL METHODS FOR EVALUATING THE DETERMINANT AND FINDING THE EIGENVALUES AND EIGENVECTORS.
DECOMPOSITION, OR FACTORING, OF SYMMETRIC MATRICES
THE JORDAN CANONICAL FORM; JORDAN DECOMPOSITION
LET A DENOTE AN n x n MATRIX WITH EIGENVALUES λ1,…,λn. THEN THERE EXISTS A NONSINGULAR MATRIX P SUCH THAT
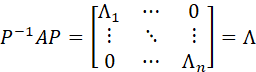
OR
![]()
WHERE
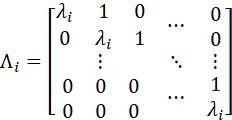
THIS DECOMPOSITION OF A IS CALLED THE JORDAN DECOMPOSITION, OR THE JORDAN CANONICAL FORM. (A DECOMPOSITION IS ALSO CALLED A FACTORING.)
IF A MATRIX A HAS DISTINCT EIGENVALUES, THEN IT MAY BE DECOMPOSED AS
![]()
A SYMMETRIC n x n REAL MATRIX A IS SAID TO BE POSITIVE DEFINITE IF xTAx IS POSITIVE FOR EVERY NON-ZERO COLUMN VECTOR x OF n REAL NUMBERS. ALTERNATIVELY, A SQUARE MATRIX A IS POSITIVE DEFINITE IF IT IS SYMMETRIC AND ALL EIGENVALUES ARE POSITIVE. A SYMMETRIX REAL MATRIX A IS SAID TO BE POSITIVE SEMIDEFINITE IF xTAx IS NONNEGATIVE FOR EVERY NON-ZERO COLUMN VECTOR x OF n REAL NUMBERS.
A TRIANGULAR MATRIX IS ONE HAVING ALL ZEROS ABOVE THE DIAGONAL (IN WHICH CASE IT IS CALLED A LOWER TRIANGULAR MATRIX) OR ALL ZEROS BELOW THE DIAGONAL (IN WHICH CASE IT IS CALLED AN UPPER TRIANGULAR MATRIX).
THE CHOLESKI DECOMPOSITION
IF A IS A POSITIVE DEFINITE n x n MATRIX, THEN THERE EXISTS A TRIANGULAR MATRIX (EITHER UPPER OR LOWER) P WITH POSITIVE MAIN DIAGONAL SUCH THAT
![]()
OR
![]()
IF P IS LOWER TRIANGULAR, THIS DECOMPOSITION IS CALLED A CHOLESKI DECOMPOSITION (OR CHOLESKI FACTORIZATION). (IF P IS LOWER TRIANGULAR, THEN P’ IS UPPER TRIANGULAR. IF P IS DENOTED BY L (FOR “LOWER”) AND P’ IS DENOTED BY U (FOR “UPPER”), THEN A = LU AND THE CHOLESKI DECOMPOSITION IS REFERRED TO AS THE “LU” DECOMPOSITION.)
SINCE ALL OF THE EIGENVALUES ARE ASSUMED POSITIVE, THE SQUARE ROOT MAY BE TAKEN OF EACH. IF WE DEFINE
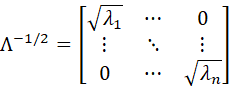
AND
![]()
THEN
![]()
AND Q IS CALLED THE SQUARE ROOT OF A AND IS DENOTED AS A-1/2.
IF A IS POSITIVE SEMIDEFINITE WITH RANK r < n, THEN THERE EXISTS A NONSINGULAR MATRIX P SUCH THAT
![]()
AND
![]()
WHERE
![]()
IF x DENOTES AN n-COMPONENT VECTOR, THEN THE VARIANCE OF A VECTOR RANDOM VARIABLE x (DENOTED BY VAR(x) OR V(x) OR var(x)) IS DEFINED TO BE THE n BY n MATRIX Σ WHOSE ij-th ELEMENT IS COV(xi, xj). THE i-th DIAGONAL ELEMENT IS THE VARIANCE OF xi. (THE VARIANCE OF A VECTOR x IS ALSO CALLED THE VARIANCE MATRIX OR THE COVARIANCE MATRIX OR THE VARIANCE-COVARIANCE MATRIX OR THE DISPERSION MATRIX.) NOTE THAT A CORRELATION MATRIX IS SYMMETRIC.CORRELATION MATRICES OF FULL RANK ARE POSITIVE DEFINITE.
IF x AND y DENOTE ANY TWO SCALAR RANDOM VARIABLES AND a DENOTES A SCALAR CONSTANT, THEN VAR(ax) = a2x AND VAR(x + y) = VAR(x) + VAR(y) + 2 COV(x,y).
IF a IS A SCALAR, WE HAVE V(ax) = a2V(x). IF a IS A VECTOR OF LENGTH n, WE HAVE V(ax) = a V(x) a’. IF A IS A MATRIX HAVING n COLUMNS, THEN V(Ax) = AV(x)A’. IF A COVARIANCE MATRIX, Σ, IS OF FULL RANK, IT IS POSITIVE DEFINITE AND HAS A UNIQUE MATRIX SQUARE ROOT, DENOTED BY Σ1/2, SUCH THAT Σ1/2Σ1/2 = Σ. NOTE THATΣ-1 = Σ-1/2Σ-1/2.
PARTITION OF A MATRIX
A PARTITIONED MATRIX IS A MATRIX WHOSE ELEMENTS ARE MATRICES. FOR EXAMPLE, IF A DENOTES AN m x n MATRIX, THEN THE MATRIX
![]()
IS A PARTITION OF MATRIX A INTO FOUR SUBMATRICES, WHERE THE NUMBER OF ROWS OF A SUBMATRIX IS THE SAME AS THAT OF A SUBMATRIX TO THE LEFT OR RIGHT, AND THE NUMBER OF COLUMNS OF A SUBMATRIX IS THE SAME AS THAT OF A SUBMATRIX ABOVE OR BELOW. PARTITIONED MATRICES MAY BE ADDED AND MULTIPLIED AS IF THEY WERE COMPOSED OF SCALARS, AS LONG AS THE COMPONENTS OF THE SUM OR PRODUCT ARE CONFORMABLE.
THE REFERENCED APPENDICES PRESENT A NUMBER OF PROPERTIES OF PARTITIONED MATRICES (I.E., EXPRESSIONS FOR INVERSES AND DETERMINANTS).
THE STACKING (vec, vech) AND KRONECKER PRODUCT OPERATORS
IF A = [aij] IS AND m x n MATRIX AND B = [bij]IS A p x q MATRIX, THEN THE KRONECKER PRODUCT (OR DIRECT PRODUCT) IF A AND B IS THE mp X nq MATRIX
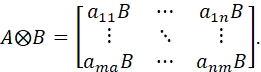
IFA = (a1,…,an) IS AN m x n MATRIX WITH m COLUMNS ai. THE vec OPERATOR (THE STACKING OPERATOR) TRANSFORMS A INTO AN mn x 1 VECTOR BY STACKING THE COLUMNS:
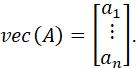
THE vech OPERATOR (THE HALF-STACKING OPERATOR) IS A STACKING OPERATOR THAT STACKS ONLY THE ELEMENTS ON OR BELOW THE MAIN DIAGONAL OF A SQUARE MATRIX. FOR EXAMPLE:
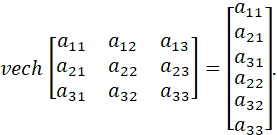
A SUMMARY OF PROPERTIES OF THE vec, vech AND KRONECKER PRODUCT OPERATORS IS PRESENTED IN TSAY (OP. CIT.). FOR EXAMPLE:
vec(A + B) = vec(A) + vec(B)
vec(AB) = (I ![]() A)vec(B) = (B’
A)vec(B) = (B’ ![]() I)vec(A).
I)vec(A).
VECTOR AND MATRIX DIFFERENTIATION
LET y BE A (REAL-VALUED) FUNCTION OF A (REAL-VALUED) VARIABLE x, DENOTED BY y = y(x) OR y = f(X). WE ASSUME THAT THE FUNCTION f(x) IS CONTINUOUS AND DIFFERENTIABLE, WITH DERIVATIVES DENOTED AS
![]()
A TAYLOR SERIES APPROXIMATION OF THE FUNCTION f ABOUT A POINT X0 IS DEFINED AS
![]()
FOR p=1 WE HAVE A LINEAR TAYLOR SERIES APPROXIMATION:
![]()
NOW, LET y = f(x) BE A (REAL-VALUED) FUNCTION OF A VECTOR x. THE GRADIENT VECTOR, OR GRADIENT OF y IS THE VECTOR OF PARTIAL DERIVATIVES:
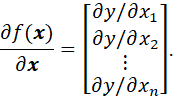
THE VECTOR SHAPE OF A DERIVATIVE (ROW OR COLUMN) IS THE SAME AS THAT OF THE DENOMINATOR OF THE DERIVATIVE.
THE SECOND DERIVATIVES MATRIX, OR HESSIAN, IS DEFINED AS

IT FOLLOWS THAT
![]()
FORMULAS AND RESULTS FROM ORDINARY (NON-VECTOR) DIFFERENTIATION HAVE ANALOGS IN VECTOR DIFFERENTIATION. THE FOLLOWING ARE SOME EXAMPLES.
IF a AND x ARE VECTOR (OF THE SAME LENGTH), THEN
![]()
IF y AND x ARE VECTORS OF LENGTH n AND A IS AN n x n MATRIX, THEN
![]()
AND
![]()
IF A IS SYMMETRIC, THEN THIS LAST EXPRESSION BECOMES
![]()
FOR MATRIX A = [aij], WE DEFINE
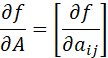
AND
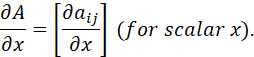
THEN WE HAVE
![]()
CHAIN RULE. LET y BE AN n x 1 VECTOR AND x BE AN m x 1 VECTOR. SUPPOSE THAT y = g(x). SUPPOSE THAT h(.) IS A p x 1 VECTOR OF FUNCTIONS gi(.) OF x. THEN
![]()
THERE ARE ALSO ANALOGOUS DIFFERENTIATION PRODUCT RULES (PRESENTED IN APPENDIX A OF TSAY (OP. CIT.).
OPTIMIZATION
CONSIDER THE PROBLEM OF FINDING A LOCAL EXTREME VALUE (OPTIMUM; MINIMUM OR MAXIMUM) VALUE OF A (REAL-VALUED) DIFFERENTIABLE FUNCTION f(x) OF A REAL VARIABLE x.
A NECESSARY CONDITION FOR A LOCAL OPTIMUM IS
![]()
A SUFFICIENT CONDITION FOR A LOCAL OPTIMUM IS
![]()
![]()
FOR A FUNCTION f(x) OF SEVERAL VARIABLES (I.E., OF A VECTOR x), THE NECESSARY CONDITION IS
![]()
AND THE SUFFICIENT CONDITION IS THAT
![]()
BE POSITIVE DEFINITE FOR A MINIMUM AND NEGATIVE DEFINITE FOR A MAXIMUM.
IN GENERAL, IT IS NECESSARY TO DETERMINE THE EIGENVALUES OF H TO DETERMINE WHETHER IT IS POSITIVE DEFINITE OR NEGATIVE DEFINITE. IF, HOWEVER, H HAS THE FORM H = A’A WHERE A IS A KNOWN MATRIX OF FULL RANK, THEN IT IS POSITIVE DEFINITE. (THIS RESULT IS USEFUL IN LEAST-SQUARES ESTIMATION, SUCH AS REGRESSION ANALYSIS.)
CONSTRAINED OPTIMIZATION
CONSIDER THE PROBLEM OF MAXIMIZING THE FUNCTION DIFFERENTIABLE f(x) OF A REAL VARIABLE x, SUBJECT TO THE CONSTRAINT c(x)=0. THIS PROBLEM MAY BE SOLVED BY THE METHOD OF LAGRANGE MULTIPLIERS. A SOLUTION SATISFIES THE CONDITION THAT THE DERIVATIVES OF THE LAGRANGIAN FUNCTION
![]()
WITH RESPECT TO x AND λ BE ZERO. THAT IS:
![]()
![]()
THE PARAMETER λ IS CALLED A LAGRANGE MULTIPLIER.
FOR MULTIPLE CONSTRAINTS, c1(x)=0, …, cp(x)=0, THERE ARE MULTIPLE LAGRANGE MULTIPLIERS, λ1,…,λp, AND, DENOTING c(x) = [ci(x)] AND λ= [λi], THE LAGRANGIAN FUNCTION IS
![]()
TO FIND THE CONSTRAINED OPTIMUM, THE DERIVATIVES WITH RESPECT TO x AND ALL OF THE λi ARE SET EQUAL TO ZERO.
FOR THE MULTIDIMENSIONAL CASE OF A VECTOR x, THE CONDITIONS ARE ANALOGOUS. THE FUNCTION TO BE OPTIMIZED IS STILL A REAL-VALUED (SCALAR) FUNCTION – THE ONLY VECTOR IS THE ARGUMENT x. THE LAGRANGIAN FUNCTION IS
![]()
IN THE VECTOR CASE, THE OPTIMAL SOLUTION SATISFIES THE EQUATIONS
![]()
![]()
THE SECOND TERM IN THE FIRST EQUATION ABOVE IS
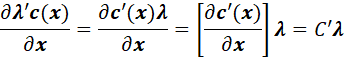
WHERE C DENOTES THE MATRIX OF DERIVATIVES OF THE CONSTRAINTS WITH RESPECT TO x.
LEAST-SQUARES ESTIMATION (THE GENERAL LINEAR STATISTICAL MODEL)
PERHAPS THE MOST WIDELY USED OF ALL STATISTICAL ESTIMATION METHODS IS THE METHOD OF LEAST SQUARES, AND IN PARTICULAR, THE METHOD OF LEAST SQUARES APPLIED TO A LINEAR MODEL.
IN THE METHOD OF LEAST SQUARES, THE MODEL ESTIMATES ARE TAKEN TO BE THOSE VALUES THAT MINIMIZE THE SUM OF SQUARES OF THE DEVIATIONS BETWEEN THE OBSERVED VALUES OF A RANDOM VARIABLE AND THE VALUES PREDICTED BY THE MODEL, I.E., THAT MINIMIZE THE MODEL ERRORS OF ESTIMATION.
UNIVARIATE LINEAR STATISTICAL MODEL
IN THE UNIVARIATE CASE, A LINEAR STATISTICAL MODEL IS DEFINED AS
y = Xβ + e
WHERE y = (y1, …, yn)’ DENOTES AN n x 1 VECTOR OF n OBSERVED VALUES OF A RESPONSE VARIABLE, β= (β1,…,βp)’ DENOTES A p x 1 VECTOR OF PARAMETERS (TO BE ESTIMATED), X DENOTES AN n x p MATRIC OF n OBSERVATIONS ON A SET OF p EXPLANATORY VARIABLES,
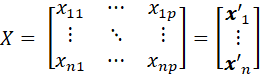
AND e = (e1,…,en)’ DENOTES AN n x 1 VECTOR OF MODEL ERROR TERMS. IN THE SIMPLEST CASE IT IS ASSUMED THAT THE MODEL ERROR TERMS ARE UNCORRELATED WITH COMMON VARIANCE σ2.
FOR THE i-th OBSERVATION, THE MODEL IS
yi = x’iβ + ei.
LET ![]() DENOTE AN ESTIMATE OF THE PARAMETER β, AND
DENOTE AN ESTIMATE OF THE PARAMETER β, AND
![]()
DENOTE THE ESTIMATE OF y
CORRESPONDING THE VALUE xi OF THE EXPLANATORY VARIABLES.
THEN THE ESTIMATED MODEL ERROR TERM, OR MODEL RESIDUAL, FOR THE i-th
OBSERVATION IS ![]() . USING THE METHOD OF LEAST SQUARES, THE GOAL IS TO
DETERMINE
. USING THE METHOD OF LEAST SQUARES, THE GOAL IS TO
DETERMINE ![]() SO THAT THE SUM OF SQUARES OF THE RESIDUALS IS
MINIMIZED.
SO THAT THE SUM OF SQUARES OF THE RESIDUALS IS
MINIMIZED.
THAT IS, MINIMIZE
![]()
OR, IN VECTOR NOTATION, MINIMIZE
![]()
THE DERIVATIVE OF THIS EXPRESSION WITH RESPECT TO β IS
![]()
SETTING THIS EQUAL TO ZERO
AND DENOTING THE SOLUTION BY ![]() PRODUCES
PRODUCES
![]()
IF XX’ IS INVERTIBLE, PREMULTIPLYING BOTH SIDES OF THIS EQUATION BY (X’X)-1YIELDS
![]()
THE GENERAL LINEAR MODEL, UNIVARIATE CASE
IN THE PRECEDING MODEL, THE MODEL ERROR TERMS WERE ASSUMED TO BE UNCORRELATED. THIS ASSUMPTION HOLDS, FOR EXAMPLE, IF THE OBSERVATIONS ARE SAMPLED INDEPENDENTLY. IN MANY APPLICATIONS, THE ASSUMPTION OF UNCORRELATEDNESS DOES NOT APPLY. FOR EXAMPLE, IN PANEL SAMPLING OBSERVATIONS TAKEN ON THE SAME HOUSEHOLD AT DIFFERENT TIMES WILL BE CORRELATED; OR OBSERVATIONS IN THE SAME SAMPLE-SURVEY CLUSTER (FIRST STAGE SAMPLE UNIT) OR STRATUM MAY BE CORRELATED.
ALSO, IN MANY APPLICATIONS THE VARIANCE OF THE MODEL ERROR TERMS IS ASSUMED TO BE THE SAME FOR ALL OBSERVATIONS. IN MANY APPLICATIONS THIS ASSUMPTION IS NOT REASONABLE.
SUPPOSE, IN GENERAL, THAT THE VARIANCE MATRIX OF THE MODEL ERROR TERMS IS Σ, AND THAT IT IS OF FULL RANK. THEN, AS DISCUSSED EARLIER, THE SQUARE ROOT MATRIX Σ1/2 IS DEFINED, SUCH THAT Σ1/2Σ1/2 = Σ AND Σ-1/2Σ1/2= I. THE TRANSFORMED VARIATE Z = Σ-1/2Y HAS VARIANCE I.
IF THE MODEL IS
y = Xβ + e
WHERE var(e) = Σ
THEN THE MODEL
z = Σ-1/2y = Σ-1/2Xβ + Σ-1/2e
SATISFIES THE CONDITIONS FOR THE LINEAR STATISTICAL MODEL HAVING UNCORRELATED MODEL ERROR TERMS, AND THE LEAST-SQUARES ESTIMATES OF THE PARAMETERS ARE
![]()
OR
![]()
THIS VERSION OF THE LINEAR STATISTICAL MODEL, WITH ARBITRARY VARIANCE MATRIX FOR THE MODEL ERROR TERMS, IS CALLED THE GENERAL LINEAR STATISTICAL MODEL (FOR THE UNIVARIATE CASE), OR SIMPLY THE GENERAL LINEAR MODEL, WITH THE WORD “STATISTICAL” UNDERSTOOD. THIS GENERAL CASE IS ALSO REFERRED TO AS THE METHOD OF WEIGHTED LEAST SQUARES.
MULTIVARIATE LINEAR STATISTICAL MODEL
THE MULTIVARIATE EXTENSION OF THE GENERAL LINEAR MODEL IS STRAIGHTFORWARD. THE MODEL IS
![]()
WHERE Z IS AN n x m MATRIX, X IS AN n x p MATRIX, B IS A p x m MATRIX, AND E IS AN n x m MATRIX. IN THIS FORMAT, THE n MULTIVARIATE OBSERVATIONS ARE THE n ROWS OF Z.
TO CAST THIS MODEL IN THE FORMAT JUST PRESENTED FOR THE UNIVARIATE CASE, THE COLUMNS OF Z ARE STACKED, YIELDING:
![]()
IN THIS FORM, THE MODEL HAS THE SAME STRUCTURE AS THE GENERAL LINEAR MODEL. NOTE THAT THERE ARE TWO TYPES OF COVARIANCES: THOSE AMONG THE m COMPONENT VARIABLES OF Z (CORRESPONDING TO THE COLUMNS OF Z), AND THOSE AMONG THE n SAMPLE OBSERVATIONS (CORRESPONDING TO THE ROWS OF Z). IT IS CLEAR TO SEE THAT THIS MODEL ALLOWS FOR AN EXTREMELY LARGE NUMBER OF PARAMETERS. A MAJOR PROBLEM IN ESTIMATION FOR THIS LINEAR MODEL IS THE IMPOSITION OF RESTRICTIONS TO REDUCE THE NUMBER OF PARAMETERS.
IF THERE IS NO CORRELATION
AMONG SAMPLE OBSERVATIONS, THEN THEVARIANCE MATRIX OF vec(E) IS ![]() , WHERE Σe DENOTES THE VARIANCE MATRIX AMONG
THE COMPONENT VARIABLES OF THE MULTIVARIATE VECTOR. IN THIS CASE IT MAY BE
SHOWN THAT THE LEAST-SQUARES ESTIMATES ARE
, WHERE Σe DENOTES THE VARIANCE MATRIX AMONG
THE COMPONENT VARIABLES OF THE MULTIVARIATE VECTOR. IN THIS CASE IT MAY BE
SHOWN THAT THE LEAST-SQUARES ESTIMATES ARE
![]()
NOTE THAT THIS EXPRESSION DOES NOT DEPEND ON Σe.
4. SOME PARTICULAR MULTIVARIATE DISTRIBUTIONS
GIVEN TWO DISCRETE RANDOM VARIABLES X AND Y, THE JOINT PROBABILITY FUNCTION IS DEFINED AS
fX,Y(x,y) = f(x,y) = P(X=x and Y=y) = P(X=x,Y=y).
GIVEN TWO CONTINUOUS RANDOM VARIABLES X AND Y, A FUNCTION f(x,y) IS A JOINT PROBABILITY DENSITY FUNCTION (PDF) IF
f(x,y)≥0 for all (x,y)
![]() and
and
for
any set A![]() R x R, P((X,Y)єA =
R x R, P((X,Y)єA = ![]()
(RECALL THAT R DENOTES THE REAL LINE.)
IN BOTH THE DISCRETE AND CONTINUOUS CASES, THE JOINT CDF IS DEFINED AS
FX,Y(x,y) = P(X≤x, Y≤Y)
THE PRECEDING DEFINITION DEFINES A JOINT DISTRIBUTION IN THE CASE OF TWO RANDOM VARIABLES. SUCH A DISTRIBUTION IS CALLED A BIVARIATE DISTRIBUTION. THIS DEFINITION MAY BE EXTENDED TO THE CASE OF MORE THAN TWO RANDOM VARIABLES. FOR EXAMPLE, GIVEN THREE DISCRETE RANDOM VARIABLES X, Y AND Z, THE JOINT PROBABILITY FUNCTION IS DEFINED AS
fX,Y,Z(x,y,z) = f(x,y,z) = P(X=x and Y=y and Z=z) = P(X=x,Y=y,Z=z).
A PROBABILITY DISTRIBUTION OF MORE THAN ONE RANDOM VARIABLE IS CALLED A MULTIVARIATE DISTRIBUTION. WHEN DEALING WITH MULTIVARIATE DISTRIBUTIONS IN GENERAL, IT IS MORE COMMON TO USE SUBSCRIPTED VARIABLE NAMES, SUCH AS x1, x2, x3,… or y1, y2, y3,… THAN SEQUENTIAL NAMES, SUCH AS x, y, z,…. IF SOME OF THE RANDOM VARIABLES ARE RESPONSE VARIABLES AND THE OTHERS ARE EXPLANATORY VARIABLES, DIFFERENT LETTERS MAY BE USED, SUCH AS y1, y2, y3,… FOR THE RESPONSE VARIABLES AND x1, x2, x3,… FOR THE EXPLANATORY VARIABLES.
MULTINOMIAL DISTRIBUTION
THE BINOMIAL DISTRIBUTION IS THE DISTRIBUTION OF THE NUMBER OF OCCURRENCES IN EACH OF TWO CATEGORIES, WHERE THE TOTAL SAMPLE SIZE IS FIXED (n).
THE PROBABILITY MASS FUNCTION FOR THE BINOMIAL DISTRIBUTION IS
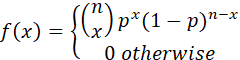
NOTATION X ~ Binomial(n,p).
THE CUMULATIVE DISTRIBUTION FUNCTION FOR THE BINOMIAL DISTRIBUTION IS:
![]()
THE EXTENSION TO MORE THAN TWO CATEGORIES IS DESCRIBED BY THE MULTINOMIAL DISTRIBUTION.
MULTINOMIAL DISTRIBUTION (CASELLA AND BURGER): LET n AND m BE POSITIVE INTEGERS AND LET p1,..., pn BE NUMBERS SATISFYING 0 ≤ pi ≤1, i = 1,...,n AND ∑pi = 1. A RANDOM VECTOR (X1,...,Xn) HAS A MULTINOMIAL DISTRIBUTION WITH m TRIALS AND CELL PROBABILITIES p1,..., pn IF ITS JOINT PROBABILITY MASS FUNCTION IS
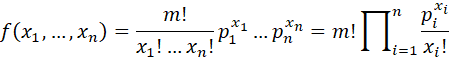
ON THE SET OF (x1,...,xn) SUCH THAT EACH xi IS A NONNEGATIVE INTEGER AND ∑xi = m.
AN EXAMPLE OF A MULTINOMIAL DISTRIBUTION IS THE NUMBER OF COUNTS IN EACH CELL OF A CROSSTABULATION, WHERE m IS THE TOTAL NUMBER OF COUNTS.
IT IS NOTED THAT ALTHOUGH THE MULTINOMIAL DISTRIBUTION IS DISCRETE, THE METHODS OF CONTINUOUS DISTRUBUTION THEORY ARE OFTEN APPLIED TO PROBLEMS INVOLVING THIS DISTRIBUTION, SUCH AS IN THE CASE OF USING A GENERALIZED LINEAR STATISTICAL MODEL (IN WHICH CASE THE DISTRIBUTION IS REPRESENTED BY AN UNDERLYING CONTINUOUS MULTIVARIATE DISTRIBUTION AND A LINK FUNCTION).
MULTIVARIATE NORMAL DISTRIBUTION
THE UNIVARIATE NORMAL (GAUSSIAN) DISTRIBUTION HAS DENSITY FUNCTION
![]()
NOTATION X ~ N(μ, σ2).
AND DISTRIBUTION FUNCTION

THIS DISTRIBUTION IS DENOTED AS N(μ,σ2) (I.E., IF X HAS A NORMAL DISTRIBUTION WITH PARAMETERS μ AND σ, X~N(μ,σ2)). THERE IS NO CLOSED-FORM EXPRESSION FOR F(x*). THE MEAN OF THE DISTRIBUTION IS μ AND THE VARIANCE IS σ2. IF μ=0 AND σ2=1, THE DISTRIBUTION IS CALLED A STANDARD NORMAL DISTRIBUTION. IF x~N(μ,σ2) THEN Z = (X – μ)/σ ~N(0,1).
THE PROBABILITY DENSITY FUNCTION OF A STANDARDIZED NORMAL RANDOM VARIABLE z IS DENOTED BY φ(z) AND THE CDF IS DENOTED BY Φ(z). TABLES OF φ(z) AND Φ(z) ARE INCLUDED IN MOST STATISTICS TEXTS.
LET -∞ <μX< ∞, -∞ <μY< ∞, 0 <σX, 0 <σY AND -1 < ρ <1 BE FIVE REAL NUMBERS. THE BIVARIATE NORMAL PDF WITH MEANS μX AND μY, VARIANCES σX2 AND σY2 AND CORRELATION ρ IS
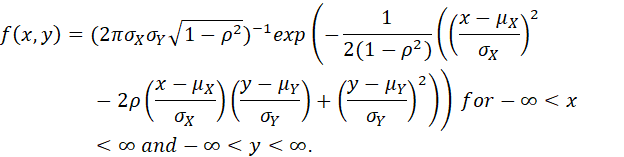
NOTE THAT IF WE DEFINE THE VECTORS
![]()
AND
![]()
AND THE MATRIX
![]()
WHERE ![]() , THEN WE MAY WRITE THE BIVARIATE NORMAL DENSITY µFUNCTION IN
VECTOR/MATRIX NOTATION AS
, THEN WE MAY WRITE THE BIVARIATE NORMAL DENSITY µFUNCTION IN
VECTOR/MATRIX NOTATION AS
![]()
WHERE
![]()
DENOTES THE DETERMINANT OF THE MATRIX Σ.
THE QUANTITIES µX AND µY ARE THE
MEANS OF X AND Y; ![]() IS THE VARIANCE OF X;
IS THE VARIANCE OF X;![]() IS THE VARIANCE OF Y; AND
IS THE VARIANCE OF Y; AND ![]() IS THE COVARIANCE OF X AND Y.
IS THE COVARIANCE OF X AND Y.
THE NORMAL DISTRIBUTION MAY BE EXTENDED TO AN ARBITRARY NUMBER OF JOINTLY DISTRIBUTED RVs. FOR MORE THAN TWO RVs, MATRIX NOTATION IS USED.
A VECTOR X = (X1,...,Xk) HAS A MULTIVARIATE NORMAL DISTRIBUTION, DENOTED AS X ~ N(μ,∑), IF ITS DENSITY FUNCTION IS
![]()
WHERE μ IS A VECTOR OF LENGTH k AND ∑ IS A k x k SYMMETRIC POSITIVE DEFINITE MATRIX. THE VECTOR μ IS THE VECTOR OF MEANS, [E(Xi)], AND THE MATRIX ∑ IS THE MATRIX OF COVARIANCES, [E(Xi – E(Xi))(Xj – E(Xj))]. THAT IS,
![]()
AND
![]()
5. MULTIVARIATE TECHNIQUES WHEN THE POPULATION PARAMETERS ARE KNOWN
THIS SECTION DESCRIBES MAJOR TOPICS IN MULTIVARIATE ANALYSIS, WHEN THE POPULATION DISTRIBUTION IS A KNOWN MULTIVARIATE NORMAL DISTRIBUTION, I.E., THE MEAN µ AND THE COVARIANCE MATRIX Σ ARE KNOWN.
MANY OF THE PROBAILITY DISTRIBUTIONS THAT ARISE IN NORMAL-BASED MULTIVARIATE ANALYSIS ARE THE SAME ONES (SUCH AS CHI-SQUARED AND FISHER’S F) THAT OCCUR IN UNIVARIATE ANALYSIS. THESE DISTRIBUTIONS HAVE BEEN DISCUSSED IN ANOTHER PRESENTATION, AND THAT DISCUSSION IS NOT REPEATED HERE.
THIS PRESENTATION IS A SURVEY OF MULTIVARIATE ANALYSIS, PRESENTING BASIC INFORMATION IN SUMMARY FORM, AND OMITTING MATHEMATICAL PROOFS. FOR A COMPLETE, DETAILED DISCUSSION OF MULTIVARIATE ANALYSIS, SEE THE BOOK BY ANDERSON (OP. CIT.).
MARGINAL AND CONDITIONAL DISTRIBUTIONS; DISTRIBUTION OF LINEAR COMBINATIONS
SOME OF THE BASIC PROPERTIES OF THE MULTIVARIATE NORMAL DISTRIBUTION ARE THE FOLLOWING:
1. THE MARGINAL DISTRIBUTION OF ONE OR MORE COMPONENTS OF A MULTIVARIATE NORMAL DISTRIBUTION IS ALSO A MULTIVARIATE NORMAL DISTRIBUTION, WITH THE SAME COMPONENT MEANS AND COVARIANCES AS THE FULL DISTRIBUTION.
2. IF X~ N(µ,Σ), THEN Y = CX, WHERE C IS A NONSINGULAR MATRIX, HAS DISTRIBUTION N(Cµ,CΣC’), I.E., Y ~ N(Cµ,CΣC’).
3. SUPPOSE THAT X~ N(µ,Σ). LET Σ1/2 DENOTE THE SQUARE ROOT MATRIX OF Σ, AND Σ-1/2 THE INVERSE OF THE SQUARE ROOT MATRIX. THEN THE DISTRIBUTION OF Y = Σ-1/2(X - µ) IS N(0,I).
4. A NECESSARY AND SUFFICIENT CONDITION THAT TWO SUBSETS OF THE RANDOM VARIABLES OF A JOINT MULTIVARIATE VECTOR BE INDEPENDENT IS THAT EACH COVARIANCE OF A VARIABLE FROM ONE SET AND A VARIABLE FROM THE OTHER SET BE ZERO.
REGRESSION AND CORRELATION
LET X~ N(µ,Σ) AND PARTITION X, HAVING p COMPONENTS, INTO TWO VECTORS HAVING q AND p – q COMPONENTS, RESPECTIVELY:
![]()
LET
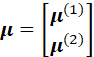
DENOTE THE CORRESPONDING PARTITION OF THE MEAN VECTOR, AND
![]()
THE CORRESPONDING PARTITION OF THE COVARIANCE MATRIX.
THEN THE CONDITIONAL DISTRIBUTION OF X(1) GIVEN X(2) IS A MULTIVARIATE NORMAL DISTRIBUTION f(x(1),x(2)) WITH MEAN
![]()
AND COVARIANCE
![]()
NOTE THAT THE COVARIANCE DOES NOT DEPEND ON MEANS.
THE QUANTITY
![]()
(I.E., THE CONDITIONAL MEAN OF X(1) GIVEN x(2)) IS CALLED THE REGRESSION FUNCTION.
THE q x p-q MATRIX ![]() IS THE MATRIX OF REGRESSION COEFFICIENTS OF X(1)
ON x(2). (THIS NOTATION IS MISLEADING. THE LETTER B IS
INTENDED TO BE AN UPPER-CASE GREEK-LETTER BETA. THAT IS,
IS THE MATRIX OF REGRESSION COEFFICIENTS OF X(1)
ON x(2). (THIS NOTATION IS MISLEADING. THE LETTER B IS
INTENDED TO BE AN UPPER-CASE GREEK-LETTER BETA. THAT IS,
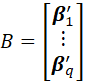
WHERE
![]()
LET σij.q+1,…,p DENOTE THE i,j-th ELEMENT OF ![]() . THESE ELEMENTS ARE CALLED PARTIAL COVARIANCES. THE
QUANTITY
. THESE ELEMENTS ARE CALLED PARTIAL COVARIANCES. THE
QUANTITY
![]()
IS CALLED THE PARTIAL CORRELATION BETWEEN Xi AND Xj HOLDING Xq+1,…,Xp FIXED.
FOR THE CASE IN WHICH THE MULTIVARIATE DISTRIBUTION CONSISTS OF JUST TWO COMPONENTS, THE PRECEDING FORMULAS REDUCE TO THE FAMILIAR FORMULAS FOR THE REGRESSION OF ONE VARIABLE ON ANOTHER.
MULTIPLE CORRELATION COEFFICIENT
CONTINUING WITH THE PRECEDING DISCUSSION, SUPPOSE THAT A MULTIVARIATE VECTOR X IS PARTITIONED AS ABOVE, INTO TWO SUBVECTORS X(1) AND X(2), AS BEFORE.
LET Xi DENOTE A COMPONENT (SINGLE RANDOM VARIABLE) OF X(1). THEN IT CAN BE PROVED THAT THE LINEAR COMBINATION αX(2) THAT MINIMIZES THE VARIANCE OF Xi - αX(2)AND THAT MAXIMIZES THE CORRELATION BETWEEN Xi AND αX(2) IS β’iX(2).
THE MAXIMUM CORRELATION BETWEEN Xi AND THE LINEAR COMBINATION αX(2) IS CALLED THE MULTIPLE CORRELATION COEFFICIENT BETWEEN Xi AND X(2).
DEFINE σ(i) AS THE i-th ROW OF Σ12. THEN IT FOLLOWS THAT THE VALUE OF THE MULTIPLE CORRELATION COEFFICIENT IS
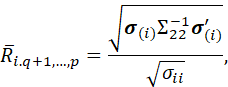
AND THE VALUE OF THE PARTIAL CORRELATION IS GIVEN BY
![]()
THE GENERAL LINEAR STATISTICAL MODEL
AS MENTIONED ABOVE, THE CONDITIONAL DISTRIBUTION OF X(1) GIVEN X(2) IS A MULTIVARIATE NORMAL DISTRIBUTION f(x(1),x(2)) WITH MEAN
![]()
AND COVARIANCE
![]()
AND THE CONDITIONAL MEAN OF X(1) GIVEN x(2) IS CALLED THE REGRESSION FUNCTION. THAT IS, THE REGRESSION FUNCTION IS
![]()
THE RIGHT-HAND SIDE OF THIS EXPRESSION IS SIMPLY A LINEAR COMBINATION OF x(2). LET US DENOTE THIS LINEAR COMBINATION AS β0 + Bx(2), WHERE β0 IS THE VECTOR OF PARAMETERS
![]()
AND B IS A MATRIX OF PARAMETERS
![]()
IN THIS NOTATION, THE REGRESSION FUNCTION BECOMES
![]()
ANY RANDOM VARIABLE, Y, THAT IS CONDITIONAL ON A VARIABLE X MAY BE WRITTEN IN THE FORM
Y = E(Y|X) + U
WHERE E(U|X) = 0. (Y AND X MAY BE SCALARS OR VECTORS OR MATRICES.) THIS FACT IS A DEFINITION OF Y, NOT A PROVED RESULT. IT CAN BE PROVED THAT THE CONDITION E(U|X) = 0 IMPLIES E(U)=0. THIS FACT FOLLOWS FROM THE LAW OF ITERATED EXPECTATIONS:
FOR ANY RANDOM VARIABLES, X, Y AND W, SUPPOSE THAT X IS A FUNCTION OF W, SAY X = f(W). THEN
![]()
(NOTE THAT THIS RESULT IS NOT THE SAME AS THE SIMPLER RESULT CONCERNING EXPECTATIONS, THAT E(Y) = E[E(Y|W)], OR, IN PARTICULAR, E(Y|X) = E[E(Y|X)|W].)
IT CAN ALSO BE PROVED THAT THE CONDITION E(U|X) = 0 IMPLIES THAT U IS UNCORRELATED WITH ANY FUNCTION OF X.
THESE RESULTS IMPLY THAT THE FACT THAT A RANDOM VARIABLE X(1)|x(2) HAS MULTIVARIATE NORMAL DISTRIBUTION N(µ1.2(x),Σ1.2) IMPLIES THAT
![]()
WHERE U ~ N(0,Σ1.2). USING THE “BETA” NOTATION JUST INTRODUCED, THIS BECOMES
![]()
THIS FORM IS A VERSION OF THE GENERAL LINEAR STATISTICAL MODEL, IN WHICH IT IS ASSUMED THAT THE MODEL ERROR TERM (U) HAS A MULTIVARIATE NORMAL DISTRIBUTION (WITH MEAN 0 AND VARIANCE Σ1.2). IN GENERAL, THE DISTRIBUTIONAL ASSUMPTIONS ABOUT THE MODEL ERROR TERM MAY BE RELAXED (E.G., BY DROPPING THE ASSUMPTION THAT IT IS MULTIVARIATE NORMAL, OR THAT THE VARIANCE FUNCTION IS THE SAME FOR ALL OBSERVATIONS). THE ESSENTIAL REQUIREMENT IS THAT U BE UNCORRELATED WITH x(2). (THE DESCRIPTOR “LINEAR” IN THE GENERAL LINEAR STATISTICAL MODEL REFERS TO THE FACT THAT THE EXPECTED VALUE IS A LINEAR COMBINATION OF THE PARAMETER B, NOT OF x(2).)
PRINCIPAL COMPONENTS
A MAJOR DIFFICULTY ASSOCIATED WITH MULTIVARIATE ANALYSIS IS THE VERY LARGE NUMBER OF PARAMETERS INVOLVED. SUPPOSE THAT WE ARE DEALING WITH A MULTIVARIATE VECTOR OF p COMPONENTS. THEN THE NUMBER OF PARAMETERS REQUIRED TO SPECIFY A p-DIMENSIONAL MULTIVARIATE NORMAL DISTRIBUTION IS p MEANS, p VARIANCES AND (p2 – p)/2 COVARIANCES, FOR A TOTAL OF (p2 -p)/2 + 2p PARAMETERS.
MULTIVARIATE PROBLEMS MAY INVOLVE MANY COMPONENTS. FOR EXAMPLE, A PSYCHOLGICAL QUESTIONNAIRE MAY INVOLVE 100 QUESTIONS. A GENERAL REPRESENTATION OF A 100-COMPONENT MULTIVARIATE NORMAL DISTRIBUTION INVOLVES (1002 – 100)/2 + 2(100) = 5,150 PARAMETERS. THIS NUMBER OF PARAMETERS IS VASTLY TOO LARGE FOR A REASONABLE MODEL. IN ORDER TO DEVELOP A REASONABLE MODEL (USEFUL MODEL OF REALITY), IT IS DESIRABLE TO REDUCE THE NUMBER OF PARAMETERS.
THE NUMBER OF PARAMETERS CAN BE REDUCED IN A NUMBER OF WAYS. THE DISTRIBUTION MAY BE SIMPLIFIED EITHER BY REDUCING THE NUMBER OF COMPONENTS OF THE MULTIVARIATE VECTOR, OR BY REDUCING THE NUMBER OF NONZERO COVARIANCES. PRIOR KNOWLEDGE OR THEORY MAY SUGGEST THAT SOME VARIABLES ARE UNCORRELATED, IN WHICH CASE THE COVARIANCES ASSOCIATED WITH THEM ARE EQUAL TO ZERO. BY EXAMINING THE CORRELATIONS AMONG VARIABLES, IT MAY BE POSSIBLE TO DISCARD SOME VARIABLES, OR TO COMBINE SIMILAR VARIABLES INTO COMPOSITE SCORES. ANOTHER METHOD IS TO TRANSFORM THE DATA IN SUCH A WAY THAT THE NUMBER OF COVARIANCES IS REDUCED.
THIS SECTION DESCRIBES A STANDARD METHODOLOGY FOR SIMPLIFYING A MULTIVARIATE DISTRIBUTION, VIZ., THE METHOD OF PRINCIPAL COMPONENTS. THE METHOD OF PRINCIPAL COMPONENTS TRANSFORMS THE ORIGINAL MULTIVARIATE VECTOR SUCH THAT THE COVARIANCES BETWEEN DIFFERENT COMPONENTS OF THE TRANSFORMED VECTOR ARE ZERO.
A MULTIVARIATE PROBABILITY DISTRIBUTION MAY BE VISUALIZED AS A MULTIDIMENSIONAL ELLIPSOID, WHERE THE ELLIPSOID IS DEFINED BY SURFACES HAVING EQUAL PROBABILITY DENSITY. IF THE COMPONENT VARIABLES ARE UNCORRELATED, THEN THE PRINCIPAL AXES OF THE ELLIPSOID ARE PARALLEL TO THE COMPONENT AXES. IF THE COMPONENT VARIABLES ARE CORRELATED, THEN THE PRINCIPAL AXES OF THE ELLIPSOID ARE OBLIQUE TO THE COMPONENT AXES.
A DISTRIBUTION OF THE LATTER TYPE (PRINCIPAL AXES OBLIQUE TO THE COMPONENT AXES) MAY BE TRANSFORMED TO THE FORMER TYPE (PRINCIPAL AXES PARALLEL TO THE COMPONENT AXES) BY A ROTATION TRANSFORMATION. A ROTATION TRANSFORMATION IS ACCOMPLISHED SIMPLY BY MULTIPLYING THE ORIGINAL (UNTRANSFORMED) MULTIVARIATE VECTOR BY A SUITABLE MATRIX. SUCH A PROCEDURE WAS DISCUSSED EARLIER IN THE SECTION DEALING WITH CONVERTING A MATRIX TO JORDAN CANONICAL FORM, OR WITH APPLYING A CHOLESKI TRANFORMATION. THE TRANSFORMED VARIABLE HAS p MEANS AND p VARIANCES, BUT ALL OF THE COVARIANCES ARE ZERO. THIS TRANSFORMATION RESULTS IN A TREMENDOUS REDUCTION IN THE NUMBER OF PARAMETERS.
ALTHOUGH THE PRINCIPAL COMPONENTS TRANFORMATION REDUCES THE NUMBER OF PARAMETERS INVOLVED, IT MAY OR MAY NOT BE A REASONABLE APPROACH TO SIMPLIFYING A MULTIVARIATE PROBLEM. IT IS BEST SUITED TO SITUATIONS WHERE THE COMPONENT VARIABLES ARE SIMILAR IN SUBSTANTIVE NATURE, SUCH AS A SET OF PSYCHOLOGICAL TEST SCORES. OTHERWISE, THE COMPONENTS OF THE TRANSFORMED VECTOR MAY BE DIFFICULT TO INTERPRET.
THE METHOD OF PRINCIPAL COMPONENTS FOCUSES ON DESCRIBING A SYSTEM SUCCINCTLY IN TERMS OF VARIANCES OF TRANSFORMED VARIABLES. IT ACCOMPLISHES THIS OBJECTIVE AT THE COST OF ELIMINATING THE INTER-CORRELATIONAL RELATIONSHIPS AMONG THE VARIABLES. THE NEXT SECTION WILL DISCUSS A PROCEDURE (FACTOR ANALYSIS) FOR SIMPLIFYING A MULTIVARIATE PROBLEM IN A WAY THAT FOCUSES ON THE INTER-RELATIONSHIPS AMONG THE ORIGINAL COMPONENT VARIABLES.
IT CAN BE PROVED THAT THE PRINCIPAL COMPONENTS ARE THE CHARACTERISTIC VECTORS OF THE COVARIANCE MATRIX. (SEE ANDERSON OP. CIT. FOR THE PROOF, WHICH INVOLVES LAGRANGIAN OPTIMIZATION OF MATRIX EXPRESSIONS.)
CANONICAL CORRELATIONS AND CANONICAL VARIABLES
IN A PRECEDING SECTION WE PRESENTED THE RESULT THAT THE MULTIPLE CORRELATION COEFFICIENT WAS THE MAXIMUM CORRELATION BETWEEN A VARIABLE Xi AND A LINEAR COMBINATION OF A SET OF COMPONENTS, X(2). THIS CONCEPT MAY BE EXTENDED. SUPPOSE THAT THE p-COMPONENT VECTOR X IS PARTITIONED INTO TWO PARTS, X(1) AND X(2), CONSISTING OF p1 AND p2 COMPONENTS, RESPECTIVELY, WHERE p1 + p2 = n. (IN THE NOTATION OF THE PREVIOUS SECTION, p1 WAS DENOTED AS q AND p2 AS p – q.)
IN THE TOPIC OF CANONICAL CORRELATIONS AND CANONICAL VARIABLES, THE PROBLEM IS TO DETERMINE LINEAR COMBINATIONS OF EACH PARTITION SUCH THAT:
1. THE FIRST LINEAR COMBINATION IN EACH PARTITION HAS MAXIMUM CORRELATION (OF THE SET OF ALL POSSIBLE LINEAR COMBINATIONS);
2. THE SECOND LINEAR COMBINATION IN EACH PARTITION HAS MAXIMUM CORRELATION, OF ALL LINEAR COMBINATIONS THAT ARE UNCORRELATED WITH THE FIRST LINEAR COMBINATIONS;
3. THE i-th SET OF LINEAR COMBINATIONS (ONE FROM EACH PARTITION) HAS MAXIMUM CORRELATION, OF ALL LINEAR COMBINATIONS THAT ARE UNCORRELATED WITH ALL PREVIOUS SETS OF LINEAR COMBINATIONS.
SAID ANOTHER WAY, THE r-th PAIR OF CANONICAL VARIATES ARE THE PAIR OF LINEAR COMBINATIONS α(r)’X(1) and γ(r)’X(2), EACH OF UNIT VARIANCE AND UNCORRELATED WITH THE FIRST r – 1 PAIRS OF CANONICAL VARIATES AND HAVING MAXIMUM CORRELATION. THE CORRELATION IS THE CANONICAL CORRELATION.
IT CAN BE SHOWN THAT THE r-th CANONICAL CORRELATION IS THE r-th LARGEST ROOT OF THE MATRIX
![]()
IN THE SPECIAL CASE OF p1 = 1, THE SINGLE CANONICAL CORRELATION IS THE MULTIPLE CORRELATION BETWEEN X(1) = X1 AND X(2).
SEE ANDERSON OP. CIT. FOR DERIVATION OF THESE RESULTS.
CLASSIFICATION ANALYSIS
CLASSIFICATION ANALYSIS IS THE PROBLEM OF DECIDING TO WHAT POPULATION (CLASS, GROUP, CATEGORY) AN INDIVIDUAL BELONGS, BASED ON MEASUREMENTS TAKEN ON THE INDIVIDUAL. IN THIS PRESENTATION, THIS PROBLEM WILL BE ADDRESSED FOR THE CASE IN WHICH THE MEASUREMENTS HAVE A MULTIVARIATE NORMAL DISTRIBUTION.
THE PROBLEM WILL BE ADDRESSED BY FIRST CONSIDERING THE CASE IN WHICH THERE EXIST JUST TWO POPULATIONS OF INTEREST. WE SHALL USE THE INDEX VALUE “1” TO REFER TO THE FIRST POPULATION AND THE VALUE “2” TO REFER TO THE SECOND POPULATION.
THIS PROBLEM IS A TWO-ALTERNATIVE STATISTICAL DECISION PROBLEM. GIVEN A SAMPLE OBSERVATION, THE STATISTICIAN (DECISIONMAKER) MUST DECIDE WHETHER THE INDIVIDUAL BELONGS TO POPULATION 1 OR POPULATION 2.
THE PROBLEM MAY BE REPRESENTED BY A 2 x 2 MATRIX, WHERE THE TWO POPULATIONS ARE REPRESENTED BY THE TWO ROWS, AND THE TWO POSSIBLE DECISIONS ARE REPRESENTED BY THE TWO COLUMNS. THE ENTRIES IN THE TABLE INDICATE WHETHER A CORRECT DECISION IS MADE.
|
Decision |
|||
|
1 |
2 |
||
|
Population |
1 |
Correct decision |
Error |
|
2 |
Error |
Correct decision |
|
THIS PROBLEM MAY BE CONSIDERED TO BE A TEST OF THE STATISTICAL HYPOTHESIS THAT THE TRUE POPULATION IS POPULATION 1. IN THAT CASE, THE ERROR OF DECIDING POPULATION 2 WHEN THE INDIVIDUAL IS FROM POPULATION 1 IS CALLED A TYPE 1 ERROR, AND THE ERROR OF DECIDING POPULATION 1 WHEN THE INDIVIDUAL IS FROM POPULATION 2 IS CALLED A TYPE 2 ERROR. THIS FRAMEWORK IS OFTEN ADOPTED IN THE APPLICATION OF MEDICAL DIAGNOSIS, WHERE POPULATION 1 IS THE POPULATION OF INDIVIDUALS HAVING AN ILLNESS OR CONDITION OF INTEREST, AND POPULATION 2 IS THE POPULATION OF INDIVIDUALS NOT HAVE THE ILLNESS OR CONDITION.
THE DECISION ABOUT WHICH POPULATION AN OBSERVED INDIVIDUAL BELONGS TO IS MADE ACCORDING TO A DECISION CRITERION, TAKING INTO ACCOUNT THE OBSERVED MEASUREMENTS. A SPECIFIED DECISION CRITERION WILL BE ASSOCIATED WITH VALUES FOR THE PROBABILITIES OF MAKING THE TWO TYPES OF ERROR. TYPICALLY, IF A DECISION CRITERION HAS A HIGHER PROBABILITY OF ONE TYPE OF ERROR, IT WILL HAVE A LOWER PROBABILITY OF THE OTHER TYPE OF ERROR.
IF THIS (HYPOTHESI-TESTING) FRAMEWORK IS ADOPTED, A STANDARD METHODOLOGY FOR SUMMARIZING THE PERFORMANCE OF ALTERNATIVE DECISION CRITERIA IS TO CONSTRUCT A GRAPH SHOWING 1 – Pr(Type 2 error) VERSUS Pr(Type 1 error) FOR MEMBERS OF THE SET OF ALTERNATIVE DECISION CRITERIA. SUCH A GRAPH IS CALLED A RECEIVER OPERATING CHARACTERISTIC GRAPH (OR CURVE), OR ROC GRAPH (OR CURVE). A PREFERRED DECISION CRITERIA IS SELECTED CORRESPONDING TO A POINT ON THE ROC CURVE.
(A DETAILED DISCUSSION OF THE USE OF ROC CURVES IS PRESENTED IN SIGNAL DETECTION THEORY AND PSYCHOPHYSICS BY DAVID M. GREEN AND JOHN A. SWETS (WILEY, 1966) OR IN EVALUATION OF DIAGNOSTIC SYSTEMS: METHODS FROM SIGNAL DETECTION THEORY BY JOHN A. SWETS AND RONALD M. PICKETT (ACADEMIC PRESS, 1982).)
FOR THIS PRESENATION WILL ADOPT A DIFFERENT FRAMEWORK, IN WHICH A COST IS ASSIGNED TO EACH OF THE TWO TYPES OF ERROR, AND THE OBJECTIVE IS TO IDENTIFY A DECISION CRITERION THAT MINIMIZES THE EXPECTED COST. (THIS IS THE APPROACH DESCIRBED IN ANDERSON OP. CIT. THIS APPROACH IS MORE COMMON IN STATISTICAL DECISION THEORY THAN THE ROC APPROACH. IT ALSO GENERALIZES MORE EASILY TO THE CASE IN WHICH THERE ARE MORE THAN TWO POPULATIONS OF INTEREST. THE ROC APPROACH IS APPROPRIATE IF THERE ARE JUST TWO POPULATIONS (E.G., PRESENCE OR ABSENCE OF A CONDITION) AND THE COSTS OF MAKING THE TWO TYPES OF ERRORS ARE NOT COMMENSURABLE (E.G., THE COST OF A FALSE POSITIVE MAY BE A MINOR EXPENSE OR INCONVENIENCE, WHEREAS THE COST OF A FALSE NEGATIVE MAY BE DEATH).
THE METHODOLOGY PRESENTED HERE USES THE SAME NOTATION AS ANDERSON.
THE SOLUTION TO THE CLASSIFICATION PROBLEM INVOLVES TWO PROBABILITY DISTRIBUTIONS: THE A PRIORI PROBABILITY THAT AN OBSERVATION IS DRAWN FROM A PARTICULAR POPULATION, AND THE CONDITIONAL PROBABILITIY DISTRIBUTION OF THE OBSERVED MEASUREMENTS, GIVEN THE POPULATION.
A PRIORI PROBABILITIES OF POPULATION MEMBERSHIP: LET q1 DENOTE THE PROBABILITY OF DRAWING AN OBSERVATION FROM POPULATION 1 AND q2 DENOTE THE PROBABILITY OF DRAWING AN OBSERVATION FROM POPULATION 2.
CONDITIONAL SAMPLING DISTRIBUTION: LET pi(x) DENOTE THE PROBABILITY DENSITY OF OBSERVATION x, GIVEN THAT IT IS DRAWN FROM POPULATION i.
COSTS OF MISSCLASSIFICATION: LET C(2|1) DENOTE THE COST ASSOCIATED WITH THE ERROR OF DECIDING POPULATION 2 WHEN THE OBSERVATION IS FROM POPULATION 1, AND C(1|2) DENOTE THE COST ASSOCIATED WITH THE ERROR OF DECIDING POPULATION 1 WHEN THE OBSERVATION IS FROM POPULATION 2.
LET Ri DENOTE THE REGION OF CLASSIFICATION FOR POPULATION i, THAT IS, THE DECISION IS MADE THAT THE OBSERVATION IS FROM POPULATION i IF THE OBSERVATION x IS IN REGION Ri.
THEN IT CAN BE PROVED THAT THE REGIONS Ri THAT CORRESPOND TO MINIMUM EXPECTED COST ARE DEFINED BY
![]()
![]()
THIS CRITERION MAY BE RECOGNIZED AS THE USUAL LIKELIHOOD-RATIO TEST OF THE HYPOTHESIS THAT THE DISTRIBUTION OF THE OBSERVED VALUE x IS p1(x) VERSUS THE ALTERNATIVE THAT IT IS p2(x).
THE PRECEDING RESULT APPLIES TO ANY PROBABILITY DISTRIBUTIONS. IN THE CASE IN WHICH THE TWO DISTRIBUTIONS ARE MULTIVARIATE NORMAL WITH DIFFERENT MEAN VECTORS BUT THE SAME COVARIANCE MATRIX, THE DENSITY FUNCTION IS
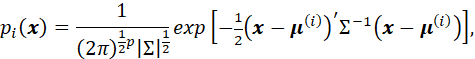
AND THE RATIO OF THE DENSITIES BECOMES
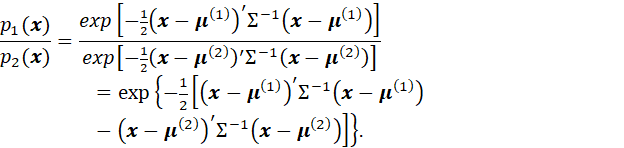
TAKING LOGARITHMS OF THE DECISION CRITERION, IT BECOMES:
![]()
![]()
WHERE
![]()
THE TERMS IN THE LEFT-HAND-SIDE OF THE INEQUALITY DEFINING THE REGIONS MAY BE REARRANGED TO PRODUCE:
![]()
![]()
THE FIRST TERM OF THE LEFT-HAND SIDE OF THE INEQUALITY,
![]()
IS CALLED THE DISCRIMINANT FUNCTION. IT IS A LINEAR FUNCTION OF THE COMPONENTS OF THE OBSERVATION VECTOR. THE SECOND TERM,
![]()
IS SIMPLY A CONSTANT (DEPENDENT ON THE DISTRIBUTION PARAMETERS).
THE PRECEDING DISCUSSION HAS DESCRIBED THE TOPIC OF CLASSIFICATION ANALYSIS IN THE CASE OF TWO POPULATIONS. EXTENSION TO THE CASE OF MORE THAN TWO POPULATIONS IS STRAIGHTFORWARD.
THE FOLLOWING RESULT IS QUOTED FROM ANDERSON:
IF qi is the a priori probability of drawing an observation from population πi = N(µ(i),Σ) (i=1,…,m) and if the costs of misclassification are equal, then the regions of classification R1,…,Rm that minimize the expected cost are defined by
![]()
and
![]()
TIME SERIES
A TIME SERIES IS A SET OF OBSERVATIONS TAKEN AT VARIOUS POINTS IN TIME (OR IN SPACE). IN MANY APPLICATIONS OF INTEREST, NEARBY OBSERVATIONS ARE CORRELATED. IN ORDER TO UNDERSTAND THE STOCHASTIC NATURE OF A SYSTEM, AND TO CONDUCT TESTS OF HYPOTHESES, IT IS HELPFUL TO TRANSFORM THE OBSERVED VARIABLES FROM ONES THAT ARE CORRELATED TO ONES THAT ARE UNCORRELATED (AND CONDUCT THE TESTS ON THE TRANSFORMED VARIABLES). SUCH A TRANSFORMATION CORRESPONDS TO A MATHEMATICAL (STATISTICAL) MODEL OF THE STOCHASTIC PROCESS THAT GENERATES THE OBSERVED DATA. THE DESIRE IS TO IDENTIFY A MODEL THAT HAS A RELATIVELY SMALL NUMBER OF PARAMETERS.
TIME SERIES MAY BE CLASSIFIED IN A NUMBER OF WAYS. ONE CLASSIFICATION IS WHETHER THE OBSERVATIONS ARE UNIVARIATE OR MULTIVARIATE. FOR UNIVARIATE OBSERVATIONS, THE CORRELATION OF INTEREST IS THE CORRELATION BETWEEN NEARBY OBSERVATIONS. FOR MULTIVARIATE OBSERVATIONS, TWO TYPES OF CORRELATIONS MAY OCCUR: CORRELATION BETWEEN NEARBY OBSERVATIONS, AND CORRELATIONS AMONG THE COMPONENT VARIABLES OF THE MULTIVARIATE OBSERVATION VECTOR.
SINCE THE 1960s MUCH WORK HAS BEEN DONE IN THE FIELD OF TIME SERIES ANALYSIS. MOST OF THE METHODOLOGY IN USE TODAY STEMS FROM THE WORK OF G. E. P. BOX AND GWILYM JENKINS, WHO SHOWED IN DETAIL HOW A PARTICULAR CLASS OF TIME-SERIES MODELS – THE AUTOREGRESSIVE INTEGRATED MOVING AVERAGE (ARIMA) MODELS – MAY BE USED TO DESCRIBE THE STOCHASTIC BEHAVIOR OF A WIDE RANGE OF TIME-VARYING PHENOMENA. THESE MODELS ARE GENERALLY KNOWN AS BOX-JENKINS MODELS.
BOX-JENKINS MODELS MAY BE UNIVARIATE OR MULTIVARIATE. THE CLASSIC TEXT ON BOX-JENKINS MODELS IS
Box, George E. P., Gwilym M. Jenkins, Gregory C. Reinsel and Greta M. Ljung, Time Series Analysis, Forecasting and Control, 5th ed., Wiley, 2016
THERE ARE A LARGE NUMBER OF TEXTS ON UNIVARIATE BOX-JENKINS MODELS. A RECENT ONE IS
Cryer, Jonathan D. and Kung-Sik Chan, Time Series Analysis with Applications in R, Springer, 2008.
MAJOR TEXTS ON MULTIVARIATE TIME SERIES ANALYSIS ARE:
Tsay, Ruey S., Multivariate Time Series Analysis with R and Financial Applications, Wiley, 2014.
Lütkepohl, Helmut, New Introduction to Multiple Time Series Analysis, Springer, 2006.
Hamilton, James D., Time Series Analysis, Princeton University Press, 1994.
IN THE UNIVARIATE CASE, A BOX-JENKINS MODEL MAY BE REPRESENTED AS
![]()
WHERE zt DENOTES AN OBSERVED VALUE AT TIME t, at IS A MODEL ERROR TERM AT TIME t, AND THE φs AND θs ARE MODEL PARAMETERS. IT IS ASSUMED THAT THE at’s HAVE ZERO MEAN AND CONSTANT VARIANCE σ2, AND ARE UNCORRELATED. (THE ASSUMPTION OF CONSTANT VARIANCE MAY BE RELAXED.)
IN THE PRECEDING EQUATION, THE “φ” TERMS (OF INDEX 1 OR GREATER) ARE REFERRED TO AS THE AUTOREGRESSIVE PART OF THE MODEL, AND THE “θ” TERMS ARE REFERRED TO AS THE MOVING AVERAGE PART OF THE MODEL.
IN THE MULTIVARIATE CASE, THE SCALARS zt AND at ARE REPLACED BY A MULTIVARIATE VECTORS AND THE φs AND θs ARE REPLACED BY MATRICES.
THIS PRESENTATION PRESENTS ONLY SUMMARY INFORMATION ABOUT TIME SERIES. THE TOPIC OF TIME SERIES ANALYSIS IS ADDRESSED IN DETAIL IN ANOTHER PRESENTATION. THE GOAL IN TIME SERIES ANALYSIS IS TO DETERMINE THE VALUES OF THE MODEL PARAMETERS, AND TO USE THE ESTIMATED MODEL TO FORECAST AND/OR CONTROL A PROCESS.
THIS SECTION HAS PRESENTED BASIC INFORMATION ABOUT THE NATURE OF A MULTIVARIATE NORMAL DISTRIBUTION, ASSUMING THAT ALL OF THE DISTRIBUTION PARAMETERS (µs and Σs) ARE KNOWN. THE NEXT SECTION ADDRESSES THE ISSUE OF ESTIMATION OF DISTRIBUTION PARAMETERS AND MAKING TESTS OF HYPOTHESIS (OR DECISIONS) ABOUT THEM.)
AS FOR THIS SECTION, THE PRIMARY REFERENCE TEXT IS ANDERSON OP. CIT.
WITH THE UBIQUITY OF GENERAL-PURPOSE STATISTICAL SOFTWARE PACKAGES, MUCH MULTIVARIATE STATISTICAL ANALYSIS IS NOW PERFORMED WITH SUPERFICIAL KNOWLEDGE OF DETAILED DISTRIBUTION THEORY AND ESTIMATION PROCEDURES. ALSO, FOR APPLICATIONS IN WHICH THE DISTRIBUTION THEORY BECOMES COMPLICATED, AS IT DOES IN MULTIVARIATE ANALYSIS, MUCH ANALYSIS IS DONE USING RESAMPLING PROCEDURES (“BOOTSTRAP” METHODS); IN SUCH CASES IT IS NOT NECESSARY TO KNOW THE EXACT FORMULA FOR A SAMPLING DISTRIBUTION. FOR THESE REASONS, THE DISCUSSION THAT FOLLOWS IS SURVEY IN NATURE, WITH MENTION OF MAJOR RESULTS AND SPECIAL CASES BUT LIMITED DISCUSSION OF DETAILS. A PRIMARY CONSIDERATION IN THE LEVEL OF DETAIL OF THE PRESENTATION IS TO PROVIDE SUFFICIENT BACKGROUND TO HAVE A HIGH-LEVEL UNDERSTANDING OF STANDARD MULTIVARIATE PROCEDURES EMPLOYED BY MAJOR STATISTICAL SOFTWARE PACKAGES.
6. ESTIMATION AND HYPOTHESIS TESTING
ESTIMATION OF THE MEAN VECTOR AND COVARIANCE MATRIX
THE FIRST PROBLEM IN NORMAL-DISTRIBUTION MULTIVARIATE ANALYSIS IS ESTIMATION OF THE PARAMETERS THAT DEFINE THE DISTRIBUTION, VIZ., THE MEAN VECTOR AND THE COVARIANCE MATRIX.
SINCE THE PARAMETRIC FORM OF THE PROBABILITY DISTRIBUTION IS SPECIFIED (I.E., IS MULTIVARIATE NORMAL), THE STANDARD APPROACH TO PARAMETER ESTIMATION IS THE METHOD OF MAXIMUM LIKELIHOOD. THAT IS, THE PARAMETER ESTIMATES ARE THOSE PARAMETER VALUES THAT MAXIMIZE THE LIKELIHOOD FUNCTION. THIS PRESENTATION WILL NOT SHOW DETAILS OF THIS PROCEDURE (WHICH ARE PRESENTED IN DETAIL IN ANDERSON).
LET x1,…,xN BE A SAMPLE OF N OBSERVATIONS FROM A MULTIVARIATE NORMAL DISTRIBUTION, N(µ,Σ), WHERE IT IS ASSUMED THAT THE NUMBER OF COMPONENTS OF xi IS p, AND p < N. THEN THE MAXIMUM LIKELIHOOD ESTIMATES OF µ AND Σ ARE
![]()
AND
![]()
THE MAXIMUM LIKELIHOOD ESTIMATE OF THE MEAN IS UNBIASED, I.E.,
![]()
THE MAXIMUM LIKELIHOOD ESTIMATE OF THE COVARIANCE MATRIX IS NOT UNBIASED. ITS EXPECTED VALUE IS
![]()
HENCE THE QUANTITY
![]()
IS AN UNBIASED ESTIMATE OF
Σ.
S IS CALLED THE SAMPLE COVARIANCE MATRIX. IT IS OFTEN DENOTED AS ![]() .
.
THE SAMPLING
DISTRIBUTION OF ![]() .
.
THE DISTRIBUTION OF ![]() IS N(µ,(1/N)Σ). HENCE THE DISTRIBUTION OF
IS N(µ,(1/N)Σ). HENCE THE DISTRIBUTION OF ![]() IS N(0, Σ). THE DISTRIBUTION OF
IS N(0, Σ). THE DISTRIBUTION OF
![]()
IS A χ2 (CHI-SQUARED) DISTRIBUTION WITH p DEGREES OF FREEDOM.
HENCE, IF Σ IS KNOWN, THE
SAMPLING DISTRIBUTION OF ![]() IS ALSO KNOWN, AND WE CAN THEN CONSTRUCT CONFIDENCE REGIONS
FOR µ IN THE USUAL WAY.
IS ALSO KNOWN, AND WE CAN THEN CONSTRUCT CONFIDENCE REGIONS
FOR µ IN THE USUAL WAY.
IF Σ IS NOT KNOWN, THEN IT CAN BE SHOWN THAT THE DISTRIBUTION OF
![]()
WHERE
![]()
IS A NONCENTRAL F
DISTRIBUTION WITH p AND N – p DEGREES OF FREEDOM AND NONCENTRALITY PARAMETER ![]() IF µ = µ0, THEN THE F DISTRIBUTION IS
CENTRAL. THESE RESULTS MAY BE USED TO CONSTRUCT CONFIDENCE REGIONS FOR µ
IN THE USUAL WAY.
IF µ = µ0, THEN THE F DISTRIBUTION IS
CENTRAL. THESE RESULTS MAY BE USED TO CONSTRUCT CONFIDENCE REGIONS FOR µ
IN THE USUAL WAY.
THE PRECEDING RESULTS ARE ANALOGUES OF THE CORRESPONDING UNIVARIATE RESULTS (z AND t STATISTICS, TESTS, AND CONFIDENCE INTERVALS).
THE SAMPLING
DISTRIBUTION OF ![]() .
.
AS MENTIONED ABOVE, THE SAMPLE COVARIANCE MATRIX IS
![]()
IN THE UNIVARIATE CASE, THIS QUANTITY HAS A χ2 DISTRIBUTION. IN THE MULTIVARIATE CASE, THIS QUANTITY HAS A GENERALIZATION OF THE χ2 DISTRIBUTION. SPECIFICALLY, THE DENSITY OF
![]()
IS
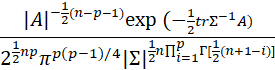
FOR A POSITIVE DEFINITE AND 0 OTHERWISE. THIS DENSITY FUNCTION IS DENOTED BY w(A|Σ,n) AND THE CORRESPONDING DISTRIBUTION FUNCTION IS DENOTED BY W(Σ,n). THIS DISTRIBUTION IS CALLED THE WISHART DISTRIBUTION WITH COVARIANCE MATRIX Σ AND n DEGREES OF FREEDOM. THE DISTRIBUTION OF S IS W((1/(N-1))Σ,N-1).
THE WISHART DISTRIBUTION ARISES OFTEN IN MULTIVARIATE ANALYSIS. IN MULTIVARIATE ANALYSIS OF VARIANCE (TO BE DISCUSSED LATER), IT IS THE DISTRIBUTION OF THE COMPONENTS OF A PARTITIONED SUM OF SQUARES.
THE DETERMINANT OF Σ, |Σ| IS CALLED THE GENERALIZED VARIANCE, AND THE DETERMINANT OF S, |S| IS CALLED THE SAMPLE GENERALIZED VARIANCE. AS DISCUSSED EARLIER, THE DETERMINANT OF A SYMMETRIC MATRIX IS A MEASURE OF VOLUME OF THE PARALLELOTROPE (HYPER-PARALLELOGRAM) SPANNED BY THE EIGENVECTORS OF THE MATRIX. ANDERSON DISCUSSES THE GENERALIZED VARIANCE AND ITS DISTRIBUTION.
SAMPLING DISTRIBUTIONS OF SAMPLE CORRELATION COEFFICIENTS, PARTIAL CORRELATION COEFFICIENTS AND MULTIPLE CORRELATION COEFFICIENTS
ANDERSON DESCRIBES ESTIMATION AND THE SAMPLING DISTRIBUTIONS OF SAMPLE CORRELATION COEFFICIENTS, PARTIAL CORRELATION COEFFICIENTS, AND MULTIPLE CORRELATION COEFFICIENTS. THOSE RESULTS ARE NOT DISCUSSED HERE.
TESTS OF HYPOTHESES ABOUT ONE OR TWO MEAN VECTORS
FOR A SINGLE SAMPLE, THE TEST OF WHETHER THE POPULATION MEAN EQUALS A SPECIFIC VALUE IS STRAIGHTFORWARD. IF THE COVARIANCE MATRIX, Σ, IS KNOWN, THEN THE SAMPLING DISTRIBUTION OF THE SAMPLE MEAN IS N(µ,Σ/n), AND THIS DISTRIBUTION MAY BE USED AS THE BASIS FOR THE TEST AND FOR CONSTRUCTION OF CONFIDENCE REGIONS. IF Σ IS UNKNOWN AND ESTIMATED BY S, THEN THE DISTRIBUTION OF T2 IS F WITH p AND n-p+1 DEGREES OF FREEDOM, AND THIS DISTRIBUTION MAY BE USED AS THE BASIS FOR THE TEST AND FOR CONSTRUCTION OF CONFIDENCE REGIONS.
FOR TWO SAMPLES (I.E., TESTING THE HYPOTHESIS OF EQUIVALENCE OF TWO POPULATION MEANS), THE SITUATION IS MORE COMPLICATED. LET µ(1) AND µ(2) DENOTE THE TWO POPULATION MEANS, AND Σ1 AND Σ2 DENOTE THE TWO POPULATION COVARIANCE MATRICES. IF Σ1 AND Σ2 ARE KNOWN, THEN THERE IS NO PROBLEM: THE DIFFERENCE IN THE SAMPLE MEANS,
![]()
IS MULTIVARIATE NORMAL WITH MEAN
![]()
AND COVARIANCE MATRIX
![]()
SINCE THE SAMPLING
DISTRIBUTION IS KNOWN, IT MAY BE USED TO MAKE TESTS ABOUT THE VALUE OF ![]() , AND TO CONSTRUCT CONFIDENCE REGIONS.
, AND TO CONSTRUCT CONFIDENCE REGIONS.
IF Σ1 AND Σ2 ARE UNKNOWN BUT EQUAL, SAY Σ1 = Σ2 = Σ, AND THE SAMPLE SIZE IS THE SAME FOR THE TWO SAMPLES IS THE SAME, n1 =n2 = n, THEN THE DIFFERENCES IN THE SAMPLE OBSERVATIONS,
![]()
HAVE A MULTIVARIATE NORMAL DISTRIBUTION WITH MEAN
![]()
AND COVARIANCE MATRIX 2Σ. THIS IS EXACTLY THE SITUATION FOR THE ONE-SAMPLE CASE (I.E., A SINGLE SAMPLE OF n OBSERVATIONS HAVING THE SAME MEAN AND VARIANCE).
FOR THE TWO-SAMPLE CASE IN WHICH THE SAMPLE SIZES ARE DIFFERENT AND THE COVARIANCE MATRIX IS UNKNOWN, HOWEVER, THIS APPROACH DOES NOT WORK. SINCE THE ESTIMATED COMMON SAMPLE VARIANCE DOES NOT HAVE A WISHART DISTRIBUTION. IN THIS CASE, THE STANDARD APPROACH IS TO ESTIMATE THE COVARIANCE MATRIX USING THE SAME NUMBER OF OBSERVATIONS FROM EACH SAMPLE, IN WHICH CASE THE ESTIMATED COMMON SAMPLE VARIANCE DOES HAVE A WISHART DISTRIBUTION.
TESTS OF HYPOTHESES ABOUT COVARIANCE MATRICES
TESTS ABOUT COVARIANCE MATRICES (E.G., WHETHER A COVARIANCE MATRIX IS EQUAL TO OR PROPORTIONAL TO A PARTICULAR MATRIX, OR WHETHER A SET OF COVARIANCE MATRICES ARE EQUAL) ARE COMPLICATED. THEY ARE BASED ON LIKELIHOOD RATIO TESTS, AND TYPICALLY INVOLVE THE CHARACTERISTIC ROOTS OF THE COVARIANCE MATRIX (OR MATRICES). THEY ARE COMPLICATED, AND NOT DISCUSSED HERE. THEY ARE DISCUSSED IN ANDERSON FOR SPECIAL CASES (E.G., TESTING WHETHER A SET OF COVARIANCES ARE EQUAL). (SINCE THE DISTRIBUTION THEORY IS COMPLICATED, SUCH TESTS MAY BE BASED ON NONPARAMETRIC METHODS, OR ON RESAMPLING.)
THE MULTIVARIATE GENERAL LINEAR STATISTICAL MODEL
ESTIMATION
IN THE UNIVARIATE CASE, THE GENERAL LINEAR STATISTICAL MODEL HAS THE FORM, FOR THE i-th OBSERVATION OF A SAMPLE,
![]()
WHERE yi IS THE OBSERVED RESPONSE, xi’ = (xi1,…,xip) ARE EXPLANATORY VARIABLES, β = (β1,…,βp)’ IS A VECTOR OF PARAMETERS, AND ei IS A MODEL ERROR TERM HAVING MEAN ZERO AND VARIANCE σ2. FOR THE MOMENT, LET US ASSUME THAT THE SAMPLE CONSISTS OF n OBSERVATIONS, AND THAT THE ei ARE UNCORRELATED (i = 1,…, n).
IN MATRIX FORM, THE SAMPLE OF OBSERVATIONS IS WRITTEN AS
![]()
WHERE y = (y1,…,yn)’ IS THE VECTOR OF OBSERVED RESPONSES, X IS A MATRIX WHOSE ROWS ARE THE SAMPLE OF EXPLANATORY VARIABLES, xi’, (i = 1,…,n), AND e = (e1,…,en)’ IS A VECTOR OF MODEL ERROR TERMS.
THE MEAN OF e IS E(e) = 0. UNDER THE ASSUMPTION THAT THE ei ARE UNCORRELATED, THE COVARIANCE MATRIX OF e IS Inσ2 (WHERE In DENOTES THE n x n IDENTITY MATRIX).
THE LEAST-SQUARES ESTIMATOR OF THE PARAMETER β IS
![]()
WHERE IT IS ASSUMED THAT THE MATRIX X’X IS INVERTIBLE.
IN MANY APPLICATIONS, THE ASSUMPTION THAT THE MODEL ERROR TERMS ARE UNCORRELATED IS REASONABLE, BUT IN MANY OTHERS, SUCH AS IN MULTIVARIATE ANALYSIS AND TIME-SERIES ANALYSIS, IT IS NOT. IF IT IS ASSUMED THAT THE COVARIANCE MATRIX OF THE MODEL ERROR TERMS IS A GENERAL (SYMMETRIC, POSITIVE DEFINITE) MATRIX Σ, THEN THE LEAST SQUARES ESTIMATOR HAS THE FORM
![]()
(THIS RESULT IS OBTAINED DIRECTLY FROM THE FIRST ONE (COVARIANCE MATRIX Inσ2) BY MAKING THE TRANSFORMATION z = Σ-1/2y, WHICH HAS COVARIANCE MATRIX I, AND USING THE EARLIER ESTIMATOR.)
THE MULTIVARIATE GENERAL LINEAR STATISTICAL MODEL IS A DIRECT EXTENSION OF THE UNIVARITE ONE. INSTEAD OF A UNIVARIATE OBSERVATION yi, WE NOW HAVE A MULTIVARIATE OBSERVATION yi COMPOSED OF k-COMPONENT VECTORS. THE PARAMETER VECTOR β MAY DIFFER FOR EACH COMPONENT (I.E., IS βi FOR THE i-th COMPONENT). WE SHALL ASSUME THAT THE ERROR TERMS FOR A PARTICULAR COMPONENT HAVE ZERO MEAND AND ARE UNCORRELATED BETWEEN DIFFERENT SAMPLE OBSERVATIONS, BUT THAT THE COVARIANCE MATRIX WITHIN SAMPLE OBSERVATIONS IS Σe, A POSITIVE DEFINITE MATRIX.
(NOTE ON NOTATION: EARLIER, WE USED p TO DENOTE THE NUMBER OF COMPONENTS OF A MULTIVARIATE VECTOR, AND WE ALSO USED p TO DENOTE THE NUMBER OF PARAMETERS IN A LINEAR MODEL, I.E., THE NUMBER OF COMPONENTS OF β. IN WHAT FOLLOWS, WE SHALL USE k TO DENOTE THE NUMBER OF COMPONENTS IN A MULTIVARIATE VECTOR, AND p TO DENOTE THE NUMBER OF COMPONENTS IN β.)
IN COMPACT FORM, THE FULL SAMPLE OF n OBSERVATIONS FOR THE MULTIVARIATE MODEL MAY BE WRITTEN AS
![]()
WHERE Y IS AN n x k MATRIX WITH ROW yi = (yi1,…,yik)’, X IS AN n x kp MATRIX (DESIGN MATRIX OR DATA MATRIX) OF EXPLANATORY VARIABLES, AND B IS A kp x k MATRIX OF PARAMETERS, AND E IS AN n x k MATRIX OF MODEL ERROR TERMS.
THIS COMPACT MULTIVARIATE FORM IS NOT THE FORM USED IN THE JUST-DESCRIBED UNIVARIATE CASE. THAT THEORY MAY BE APPLIED TO THE MULTIVARIATE CASE BY CONCATENATING THE SAMPLE VECTORS INTO A SINGLE COLUMN VECTOR. THAT IS, THE PRECEDING MODEL MAY BE WRITTEN IN “STACKED” FORM AS
![]()
DETERMINATION OF THE LEAST-SQUARES ESTIMATE FOR THE PARAMETER PROCEEDS IN THE SAME WAY AS USUAL, VIZ., BY MINIMIZING THE ERROR SUM OF SQUARES (BY SETTING PARTIAL DERIVATIVES OF THE ERROR SUM OF SQUARES EQUAL TO ZERO).
SOME MATRIX MANIPULATIONS SHOW THAT THE LEAST-SQUARES ESTIMATOR FOR THIS MODEL IS
![]()
THIS IS THE SAME FORM AS FOR THE UNIVARIATE CASE, WHERE THE n x 1 VECTOR y HAS BEEN REPLACED BY THE n x k MATRIX Y AND THE DATA/DESIGN MATRIX X IS NOW AN n x kp MATRIX INSTEAD OF AN n x p MATRIX.
NOTE THAT THE SOLUTION DOES NOT INVOLVE THE MATRIX Σe. THE REASON FOR THIS IS THE ASSUMPTION THAT THERE IS NO CORRELATION BETWEEN VARIABLES IN DIFFERENT OBSERVATIONS. THE ESTIMATES MAY BE DETERMINED SEPARATELY FOR EACH COMPONENT VARIABLE OF THE MULTIVARIATE VECTOR IN THE USUAL FASHION, USING EXACTLY THE SAME COMPUTATIONAL PROCEDURES AS IN THE UNIVARIATE CASE. THIS SITUATION IS REFERRED TO AS “SEEMINGLY UNRELATED REGRESSIONS.”
AS BEFORE, DEFINE THE
MODEL RESIDUALS ![]() TO BE THE DIFFERENCES BETWEEN THE OBSERVED VALUES AND
THE VALUES PREDICTED BY THE MODEL BY SUBSTITUTING THE LEAST-SQUARES ESTIMATES
IN THE MODEL EQUATION. LET
TO BE THE DIFFERENCES BETWEEN THE OBSERVED VALUES AND
THE VALUES PREDICTED BY THE MODEL BY SUBSTITUTING THE LEAST-SQUARES ESTIMATES
IN THE MODEL EQUATION. LET ![]() DENOTE THE SAMPLE COVARIANCE MATRIX DEFINED BY
DENOTE THE SAMPLE COVARIANCE MATRIX DEFINED BY
![]()
THEN IT CAN BE SHOWN THAT
THE LEAST-SQUARES ESTIMATE ![]() IS UNBIASED (
IS UNBIASED (![]() ); THE ESTIMATE
); THE ESTIMATE ![]() IS UNBIASED (
IS UNBIASED (![]() ;
; ![]() AND
AND ![]() ARE UNCORRELATED; AND THE COVARIANCE MATRIX OF THE
(STACKED) PARAMETER ESTIMATES IS
ARE UNCORRELATED; AND THE COVARIANCE MATRIX OF THE
(STACKED) PARAMETER ESTIMATES IS
![]()
THE LEAST-SQUARES
ESTIMATES DO NOT DEPEND ON ANY DISTRIBUTIONAL ASSUMPTIONS ABOUT THE MODEL ERROR
TERMS, OTHER THAN THEIR HAVING ZERO MEAN, NO CORRELATION BETWEEN OBSERVATIONS,
AND COVARIANCE MATRIX ![]() WITHIN OBSERVATIONS. IF IT IS ALSO ASSUMED THAT THE ERROR
TERMS HAVE A MULTIVARIATE NORMAL DISTRIBUTION, THEN IT CAN BE SHOWN THAT THE
MAXIMUM LIKELIHOOD ESTIMATE
WITHIN OBSERVATIONS. IF IT IS ALSO ASSUMED THAT THE ERROR
TERMS HAVE A MULTIVARIATE NORMAL DISTRIBUTION, THEN IT CAN BE SHOWN THAT THE
MAXIMUM LIKELIHOOD ESTIMATE ![]() OF B IS THE SAME AS THE LEAST-SQUARES ESTIMATE; THAT
THE MAXIMUM LIKELIHOOD ESTIMATE OF Σe IS
OF B IS THE SAME AS THE LEAST-SQUARES ESTIMATE; THAT
THE MAXIMUM LIKELIHOOD ESTIMATE OF Σe IS ![]() ; THAT (n-p)
; THAT (n-p) ![]() HAS A WISHART DISTRIBUTION Wk,n-(k+1)p-1; THAT
HAS A WISHART DISTRIBUTION Wk,n-(k+1)p-1; THAT
![]() IS NORMALLY DISTRIBUTED WITH MEAN
IS NORMALLY DISTRIBUTED WITH MEAN ![]() AND COVARIANCE MATRIX
AND COVARIANCE MATRIX ![]() ;
; ![]() IS INDEPENDENT OF
IS INDEPENDENT OF ![]() . FURTHERMORE, THE ESTIMATES ARE ASYMPTOTICALLY
NORMALLY DISTRIBUTED (SEE TSAY FOR MORE DETAILS.) THESE RESULTS MAY BE USED TO
PERFORM TESTS OF HYPOTHESIS AND CONSTRUCT CONFIDENCE INTERVALS.
. FURTHERMORE, THE ESTIMATES ARE ASYMPTOTICALLY
NORMALLY DISTRIBUTED (SEE TSAY FOR MORE DETAILS.) THESE RESULTS MAY BE USED TO
PERFORM TESTS OF HYPOTHESIS AND CONSTRUCT CONFIDENCE INTERVALS.
TESTS OF HYPOTHESIS AND CONFIDENCE REGIONS
FOR THE GENERAL LINEAR MODEL, TESTS OF HYPOTHESIS (AND CONFIDENCE REGIONS) ARE CONSTRUCTED USING THE LIKELIHOOD RATIO CRITERION. MANY OF THE TESTS IN THE MULTIVARIATE CASE ARE ANALOGOUS TO THOSE OF THE UNIVARIATE CASE, SUCH AS TESTING WHETHER REGRESSION PARAMETERS ARE EQUAL TO ZERO. THE ADDITIONAL COMPLEXITY OF THE MULTIVARIATE MODEL LEADS TO ADDITIONAL KINDS OF TEST, SUCH AS TESTS ABOUT MATRICES OF REGRESSION COEFFICIENTS.
SEE ANDERSON FOR DISCUSSION OF THE TOPIC OF TESTS OF HYPOTHESIS AND CONFIDENCE REGIONS IN THE MULTIVARIATE CASE.
MULTIVARIATE ANALYSIS OF VARIANCE AND ANALYSIS OF COVARIANCE
THE GENERAL LINEAR MODEL INCLUDES THE METHODOLOGIES OF ANALYSIS OF VARIANCE AND ANALYSIS OF COVARIANCE AS SPECIAL CASES. ANALYSIS OF VARIANCE ADDRESSES LINEAR MODELS IN WHICH EXPLANATORY VARIABLES ARE CATEGORICAL. ANALYSIS OF COVARIANCE ADDRESSES LINEAR MODELS IN WHICH MAJOR EXPLANATORY VARIABLES ARE CATEGORICAL, AND A FEW VARIABLES ARE CONTINUOUS. THESE METHODOLOGIES ARE USED IN EXPERIMENTAL DESIGNS, WHERE THE EXPERIMENTER HAS CONTROL OVER THE MAIN EXPLANATORY VARIABLES. FOR THESE METHODOLOGIES, RESULTS ARE PRESENTED IN SPECIAL TABLES (VIZ., ANALYSIS OF VARIANCE TABLES AND ANALYSIS OF COVARIANCE TABLES).
THESE TOPICS ARE NOT ADDRESSED IN THIS PRESENTATION (EITHER IN THE UNIVARIATE CASE OR THE MULTIVARIATE CASE), BUT MAY BE THE SUBJECT OF A FUTURE PRESENTATION (ON EXPERIMENTAL DESIGN).
TESTS FOR INDEPENDENCE
A PROBLEM THAT ARISES IN MULTIVARIATE IS THAT OF DIVIDING A MULTIVARIATE VECTOR INTO SETS OF VARIATES, AND TESTING WHETHER THE SETS ARE MUTUALLY INDEPENDENT, I.E., WHETHER EACH MEMBER OF ONE SET IS UNCORRERATED WITH EACH VARIABLE OF ANOTHER SET.
THE METHODOLOGY FOR MULTIVARIATE TESTS FOR INDEPENDENCE IS SIMILAR TO THAT FOR THE TESTS OF HYPOTHESIS FOR THE MULTIVARIATE GENERAL LINEAR MODEL. FOR THE MULTIVARIATE NORMAL DISTRIBUTION, A TEST OF INDEPENDENCE MAY BE FORMULATED AS A TEST ABOUT THE STRUCTURE OF THE COVARIANCE MATRIX, I.E., WHETHER CERTAIN SUBMATRICES ARE ZERO. THE LIKELIHOOD RATIO PROCEDURE IS USED TO CONSTRUCT A TEST. THE TESTS MAY BE FORMULATED IN TERMS OF GENERALIZED VARIANCES.
SEE ANDERSON FOR DETAILS.
PRINCIPAL COMPONENTS ANALYSIS
A FUNDAMENTAL DIFFICULTY WITH MULTIVARIATE ANALYSIS IS THE LARGE NUMBER OF PARAMETERS INVOLVED IN MULTIVARIATE MODELS. AS MENTIONED EARLIER, THE NUMBER OF PARAMETERS IN A BASIC k-DIMENSIONAL MULTIVARIATE NORMAL DISTRIBUTION IS k MEANS, k VARIANCES AND (k2 – k)/2 COVARIANCES, FOR A TOTAL OF (k2 -k)/2 + 2k PARAMETERS. A MULTIVARIATE GENERAL LINEAR MODEL THAT INCLUDES p EXPLANATORY VARIABLES INCLUDES pk PARAMETERS FOR THE MEAN. IF THERE IS NO INTERCORRELATION AMONG SAMPLE OBSERVATIONS, THEN THE NUMBER OF VARIANCES AND COVARIANCES IS THE SAME AS FOR THE BASIC MULTIVARIATE DISTRIBUTION, BUT IF THERE ARE CORRELATIONS AMONG SAMPLE OBSERVATIONS (AS IS THE CASE IN TIME SERIES ANALYSIS), THE NUMBER OF PARMATERS MAY BE MUCH LARGER.
MODELS HAVING LARGE NUMBER OF PARAMETERS POSSESS AN INHERENT DANGER FOR MANY APPLICATIONS (SUCH AS FORECASTING), IN THAT THE MODEL MAY FIT THE DATA WELL AND YET FORECAST POORLY. IT IS USEFUL, THEREFORE, TO APPLY METHODS TO SIMPLIFY THE MODELS. THIS CAN BE DONE IN A NUMBER OF WAYS, SUCH AS BY MAKING SIMPLIFYING ASSUMPTIONS (JUSTIFIED BY SUBSTANTIVE THEORY) OR BY COMBINING VARIABLES OR ELIMINATING VARIABLES.
WITH RESPECT TO COMBINING VARIABLES AND DROPPING VARIABLES, A POWERFUL TOOL IS THE METHOD OF PRINCIPAL COMPONENTS. AS DISCUSSED EARLIER, THE METHOD OF PRINCIPAL COMPONENTS IS THE APPLICATION OF A LINEAR TRANSFORMATION OF THE ORIGINAL MULTIVARIATE VECTOR TO A NEW VECTOR HAVING USEFUL STATISTICAL PROPERTIES. SPECIFICALLY, THE ORIGINAL COORDINATE SYSTEM IS ROTATED IN SUCH A WAY THAT THE FIRST VARIABLE OF THE NEW COORDINATE SYSTEM HAS MAXIMUM VARIANCE, THE SECOND VARIABLE HAS MAXIMUM VARIANCE OUT OF ALL VARIABLES ORTHOGONAL TO THE FIRST VARIABLE, THE THIRD VARIABLE HAS MAXIMUM VARIANCE OUT OF ALL VARIABLES ORTHOGONAL TO THE FIRST TWO, AND SO ON.
THE EARLIER DISCUSSION ADDRESSED THE ISSUE OF PRINCIPAL COMPONENTS IN THE POPULATION, I.E., IT WAS ASSUMED THAT THE PARAMETERS OF THE MULTIVARIATE DISTRIBUTION WERE KNOWN. THIS SECTION ADDRESSES THE SITUATION IN WHICH THE DISTRIBUTION PARAMETERS ARE ESTIMATED.
THE PRINCIPAL COMPONENTS ARE THE EIGENVECTORS OF THE COVARIANCE MATRIX, WHERE THE LENGTH OF EACH EIGENVECTOR IS THE CORRESPONDING EIGENVALUE. THE EIGENVALUES ARE THE SOLUTIONS (λ1,…,λp) TO THE EQUATION
![]()
AND THE EIGENVECTORS ARE THE SOLUTIONS (b1,…,bp) TO THE EQUATION
![]()
LET US DEFINE THE MATRIX Λ AS
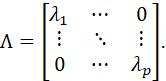
THE PROBLEM IS TO ESTIMATE ALL OF THE PARAMETERS µ, Σ, Λ AND B = (b1,…,bp). THIS IS DONE, AS USUAL, BY THE METHOD OF MAXIMUM LIKELIHOOD.
IT IS A FACT THAT THE
MAXIMUM LIKELIHOOD ESTIMATOR OF A FUNCTION OF A PARAMETER IS THE FUNCTION OF
THE MAXIMUM LIKELIHOOD ESTIMATOR OF THE PARAMETER. SINCE Λ AND B ARE
FUNCTIONS OF µ AND Σ, IT FOLLOWS THAT THE MAXIMUM LIKELIHOOD ESTIMATORS OF
Λ
AND B ARE OBTAINED USING THE SAME EQUATIONS GIVEN ABOVE FOR DETERMINING Λ AND B, SIMPLY
BY REPLACING µ AND Σ BY THEIR MAXIMUM LIKELIHOOD ESTIMATORS (![]() AND
AND ![]() ).
).
AS DISCUSSED EARLIER, THE METHOD OF PRINCIPAL COMPONENTS IS A METHOD OF ROTATING THE AXES OF A MULTIVARIATE DISTRIBUTION (I.E., TRANSFORMING THE COMPONENT VARIABLES OF A MULTIVARIATE VECTOR) SUCH THAT THE FIRST PRINCIPAL COMPONENT HAS MAXIMUM VARIANCE, THE SECOND PRINCIPAL COMPONENT HAS MAXIMUM VARIANCE, OUT OF ALL VARIABLES ORTHOGONAL TO THE FIRST, AND SO ON.
SINCE THE MATRIX TRANSFORMATIONS INVOLVED IN THE METHOD OF PRINCIPAL COMPONENTS ARE ORTHONORMAL, THE DETERMINANT OF THE COVARIANCE MATRICES OF THE ORIGINAL AND TRANSFORMED VARIABLES HAS THE SAME VALUE. ALSO, THE TRACE OF THE COVARIANCE (SUM OF THE DIAGONAL ENTRIES, AND ALSO THE SUM OF THE CHARACTERISTIC ROOTS) HAS THE SAME VALUE. THE METHOD OF PRINCIPAL COMPONENTS IS SIMPLY A METHOD OF TRANSFORMING VARIABLES TO NEW VARIABLES IN SUCH A WAY THAT THE TOTAL VARIANCE (AS REPRESENTED BY THE TRACE) IS DECOMPOSED.
FROM AN INFORMATION-THEORETIC VIEWPOINT, THE AMOUNT OF INFORMATION ASSOCIATED WITH A VARIABLE IS INVERSELY PROPORTIONAL TO THE VARIANCE OF THE VARIABLE.
A DIFFICULTY WITH TRANSFORMED VARIABLES IS THEIR INTERPRETATION. THE METHOD OF PRINCIPAL COMPONENTS IS APPROPRIATE FOR TRANSFORMING VARIABLES OF A COMMON METRIC, FOR WHICH THE LINEAR COMBINATIONS OF THE VARIABLES HAVE A REASONABLE MEANING (INTERPRETATION). FOR EXAMPLE, A SET OF 15 MEASURMENTS MAY BE TAKEN ON ANIMAL SKULLS. USING THE METHOD OF PRINCIPAL COMPONENTS, IT MAY BE TURN OUT THAT THE FIRST PRINCIPAL COMPONENT IS APPROXIMATELY EQUAL TO THE SUM OF THE HEIGHT, WIDTH AND DEPTH OF THE SKULL, AND THAT THE OTHER PRINCIPAL COMPONENTS ARE VERY SMALL. THAT IS, MOST OF THE VARIATION IN SKULL DIMENSIONS IS SUMMARIZED IN THIS SINGLE VARIABLE. IN SOME APPLICATIONS, THE ORIGINAL 15 MEASUREMENTS MAY BE REPLACED BY A SINGLE VARIABLE, WHICH CONTAINS MOST OF THE INFORMATION INHERENT IN THE ORIGINAL 15 VARIABLES.
FACTOR ANALYSIS
IN THE METHOD OF PRINCIPAL COMPONENTS, INTEREST FOCUSSES ON THE LARGER CHARACTERISTIC ROOTS. IF THE GOAL IS TO SIMPLIFY A PROBLEM BY REDUCING THE NUMBER OF COMPONENTS OF THE MULTIVARIATE VECTOR, THEN ONE APPROACH IS TO DISCARD VARIABLES ASSOCIATED WITH THE SMALLER CHARACTERISTIC ROOTS. THIS MAY BE DONE IN AN AD HOC MANNER, BUT A MORE STANDARD PROCEDURE IS THE METHOD OF FACTOR ANALYSIS.
IN FACTOR ANALYSIS IT IS ASSUMED THAT THE MULTIVARIATE VECTOR X MAY BE REPRESENTED AS
![]()
WHERE f IS AN m-COMPONENT VECTOR OF NONOBSERVABLE FACTOR SCORES, µ IS A VECTOR OF MEANS, AND U IS A VECTOR OF NONOBSERVABLE ERRORS. THE p x m MATRIX Λ (m < p) IS CALLED A MATRIX OF FACTOR LOADINGS. IT IS ASSUMED THAT f IS A RANDOM VARIABLE WITH E(f) = 0 AND Eff’ = M; IT IS ALSO ASSUMED THAT E(U) = 0 AND E(UU’) = Ψ, A DIAGONAL MATRIX, AND E(fU’) = 0.
UNDER THESE ASSUMPTIONS E(X) = µ AND
![]()
A PROBLEM WITH THIS MODEL IS THAT IT IS NOT KNOWN WHAT COVARIANCE MATRICES CAN BE REPRESENTED BY THE PRECEDING EXPRESSION OF GIVEN m, AND IF SUCH MATRICES EXIST, WHAT RESTRICTIONS ON Λ AND M MAKE THEM UNIQUE. IN OTHER WORDS, THERE MAY NOT EXIST A MULTIVARIATE NORMAL RANDOM VARIABLE X SATISFYING THE PRECEDING MODEL.
TO ADDRESS THIS ISSUE, THE ASSUMPTION OF NORMALITY OF X MUST BE DROPPED. A VARIETY OF METHODS MAY BE USED TO ESTIMATE THE PARAMETERS OF THE FACTOR MODEL (Λ, M AND Ψ). THE METHOD OF MAXIMUM LIKELIHOOD MAY BE USED, BUT PROBLEMS ARE ENCOUNTERED SINCE THE MODEL IS NOT UNIQUE (I.E., THERE ARE MANY ALTERNATIVE REPRESENTATIONS, OR SELECTIONS OF FACTORS f). ALTERNATIVE ESTIMATION METHODS INCLUDE THE CENTROID METHOD AND THE METHOD OF PRINCIPAL COMPONENTS.
DESPITE THESE PROBLEMS, CONSIDERABLE USE IS MADE OF THE PRECEDING MODEL. FOR THE PROBLEM OF DECIDING WHICH VARIABLES TO DISCARD FROM A MULTIVARIATE VECTOR WITH RELATIVELY LITTLE REDUCTION IN THE TOTAL VARIANCE, IT IS USED TO DETERMINE A REASONABLE VALUE FOR m. A PRIMARY CONSIDERATION IN FACTOR ANALYSIS IS THE IDENTIFICATION OF FACTORS (LINEAR COMBINATIONS OF THE ORIGINAL VARIABLES) THAT HAVE A REASONABLE MEANING. IN THE SEARCH FOR SUCH REPRESENTATIONS, A VARIETY OF AXIS ROTATIONS MAY BE CONSIDERED.
THE REFERENCES PROVIDED EARLIER BY LAWLY AND MAXWELL, AND BY HARMON, MAY BE CONSULTED FOR ADDITIONAL DETAILS ON THIS METHOD.
CANONICAL CORRELATION
ESTIMATION OF CANONICAL
CORRELATIONS AND CANONICAL VARIATES PROCEEDS BY MAKING THE SAME CALCULATIONS ON
THE SAMPLE CORRELATION MATRIX, ![]() , AS ARE USED TO OBTAIN THE POPULATION CANONICAL
CORRELATIONS.
, AS ARE USED TO OBTAIN THE POPULATION CANONICAL
CORRELATIONS.
CLASSIFICATION ANALYSIS
IN THE PRECEDING DISCUSSION OF CLASSIFICATION ANALYSIS, A PROCEDURE WAS PRESENTED THAT MINIMIZES THE EXPECTED COST OF MISCLASSIFICATION. THE CLASSIFICATION CRITERION WAS BASED ON KNOWN PROBABILITIES. IT CANNOT BE PROVED, HOWEVER, THAT THE DESCRIBED PROCEDURE MINIMIZES THE EXPECTED COST IN THE CASE WHERE THE PROBABILITIES ARE ESTIMATED. THE CRITERION APPEARS REASONABLE, HOWEVER, AND IS USED.
MULTIVARIATE TIME SERIES MODELS (SUMMARY)
A PRECEDING SECTION DESCRIBED THE CLASS OF BOX-JENKINS MODELS, WHICH ARE USED AS A BASIS FOR FORECASTING AND CONTROL IN BOTH THE UNIVARIATE AND MULTIVARIATE CASES. DETAILED DISCUSSION OF THE PROCEDURES FOR DEVELOPING BOX-JENKINS MODELS IS THE SUBJECT OF A SEPARATE PRESENTATION.
THE METHODOLOGY FOR ESTIMATING A MULTIVARIATE BOX-JENKINS MODEL FROM SAMPLE DATA PARALLELS THAT FOR A UNIVARIATE MODEL. IT MAKES HEAVY USE OF LEAST-SQUARES THEORY, AND ITERATIVE APPLICATION OF THE STEPS OF MODEL IDENTIFICATION, ESTIMATION AND TESTING.
WHILE MUCH OF THE METHODOLOGY IS SIMILAR IN THE MULTIVARIATE AND UNIVARIATE CASES, THERE ARE SOME DIFFERENCES. ONE AREA OF DIFFERENCE INVOLVES THE FORECASTING ONCE COMPONENT OF A MULTIVARIATE VECTOR, CONDITIONAL ON THE VALUES OF OTHER COMPONENTS. THE PROBLEM THAT ARISES IS THAT IF A FUTURE VALUE OF ONE COMPONENT IS SPECIFIED, IT IS NOT REASONABLE TO BELIEVE THAT THE OTHER VARIABLES MAY BE HELD CONSTANT, IF THE VARIABLES ARE CORRELATED. AN APPROACH TO HANDLING THIS PROBLEM IS TO APPLY THE MULTIVARIATE PROCEDURE OF PRINCIPAL COMPONENTS TO ORTHOGONALIZE THE VECTOR SO THAT THE COMPONENTS ARE ORTHOGONAL. IN THAT CASE, IT IS REASONABLE TO CONDITION ON ONE OF THEM, HOLDING THE OTHERS FIXED. AS USUAL, THIS APPROACH IS USEFUL IF A MEANINGFUL INTERPRETATION CAN BE GIVEN TO THE TRANSFORMED VARIABLES.
FndID(206)
FndTitle(CONTINUOUS MULTIVARIATE ANALYSIS: LECTURE NOTES)
FndDescription(CONTINUOUS MULTIVARIATE ANALYSIS: LECTURE NOTES)
FndKeywords(multivariate analysis; statistics course; short course)