MULTIVARIATE TIME SERIES ANALYSIS: LECTURE NOTES
Version without figures.
9 August 2018
Joseph George Caldwell, PhD (Statistics)
1432 N Camino Mateo, Tucson, AZ 85745-3311 USA
Tel. (001)(520)222-3446, E-mail jcaldwell9@yahoo.com
Website http://www.foundationwebsite.org
Copyright © 2018 Joseph George Caldwell. All rights reserved.
Contents
2. SUMMARY OF SINGLE-VARIABLE UNIVARIATE TIME SERIES ANALYSIS. 4
MAJOR FEATURES OF TIME SERIES. 5
THEORETICAL MODELS: WHITE NOISE, AUTOREGRESSIVE, MOVING AVERAGE, ARMA, ARIMA, SEASONAL 11
HOMOGENEOUS NONSTATIONARY PROCESS. 16
IMPULSE RESPONSE FUNCTION (IRF) 19
STATIONARITY TRANSFORMATIONS, TESTS OF HYPOTHESES. 20
MEASURES OF MODEL EFFICIENCY (INFORMATION CRITERIA): AIC, BIC, HQC. 28
GENERAL FORM OF AN ARIMA MODEL. 30
ALTERNATIVE FORMS OF AN ARIMA MODEL. 31
IMPULSE RESPONSE FUNCTION.. 40
ALTERNATIVE REPRESENTATIONS: UNIQUENESS OF MODEL, JOINT PDF, ACF (NORMAL). 41
ALTERNATIVE REPRESENTATIONS: STATE SPACE, KALMAN FILTER. 42
DETAILED EXAMPLE OF THE DEVELOPMENT OF A SINGLE-VARIABLE UNIVARIATE TIME SERIES MODEL. 43
3. SUMMARY OF MULTIVARIABLE UNIVARIATE MODELS (TRANSFER FUNCTION MODELS, DISTRIBUTED LAG MODELS). 54
A DISCRETE LINEAR TRANSFER FUNCTION MODEL. 59
FEATURES OF TRANSFER FUNCTION MODELS. 61
IDENTIFICATION OF TRANSFER-FUNCTION MODELS, USING THE CROSS-CORRELATION FUNCTION; PREWHITENING 64
ESTIMATION OF PARAMETERS OF TRANSFER-FUNCTION MODELS. 67
MEASURES OF MODEL EFFICIENCY. 70
PROCESS CONTROL; POLICY ANALYSIS. 71
IMPULSE RESPONSE FUNCTION.. 72
PREDICTION (FORECAST ERROR) VARIANCE DECOMPOSITION.. 72
DETAILED EXAMPLE OF DEVELOPMENT AND APPLICATION OF A BIVARIATE TRANSFER-FUNCTION MODEL 72
4. GENERAL MULTIVARIATE TIME SERIES ANALYSIS. 72
MULTIVARIATE TIME SERIES DESCRIPTORS. 74
NONSTATIONARITY AND COINTEGRATION.. 88
STATIONARITY TRANSFORMATIONS AND TESTS (FOR HOMOGENEITY, COINTEGRATION) 92
MEASURES OF MODEL EFFICIENCY. 97
FORECASTING (UNCONDITIONAL VS. CONDITIONAL) 97
FORECAST ERROR VARIANCE DECOMPOSITION.. 97
ALTERNATIVE REPRESENTATIONS: STATE SPACE, KALMAN FILTER. 99
ALTERNATIVES TO THE GAUSSIAN DISTRIBUTION; COPULAS. 99
DETAILED EXAMPLE OF A MULTIVARIATE TIME SERIES ANALYSIS APPLICATION.. 101
5. TIME SERIES ANALYSIS SOFTWARE. 102
1. OVERVIEW
THIS PRESENTATION IS A SURVEY OF THE BASIC CONCEPTS OF DISCRETE MULTIVARIATE TIME SERIES ANALYSIS. IT BUILDS ON MATERIAL PRESENTED IN OTHER PRESENTATIONS ON DISCRETE UNIVARIATE TIME SERIES ANALYSIS AND CONTINUOUS MULTIVARIATE STATISTICAL ANALYSIS.
THE PRESENTATION PRESENTS KEY RESULTS, BUT NOT MATHEMATICAL PROOFS. MATHEMATICAL DETAILS ARE PRESENTED IN THE FOLLOWING REFERENCES.
BOX, G. E. P., AND GWILYM JENKINS, TIME SERIES ANALYSIS, FORECASTING CONTROL, FIRST EDITION HOLDEN-DAY, 1970, LATEST ADDITION IS 5TH EDITION BY GEORGE E. P. BOX, GWILYM M. JENKINS, GREGORY C. REINSEL AND GRETA M. LJUNG, WILEY, 2016. (IN THIS PRESENTATION, THIS REFERENCE WILL BE REFERRED TO AS BJRL.)
TSAY, RUEY S., MULTIVARIATE TIME SERIES ANALYSIS WITH R AND FINANCIAL APPLICATIONS, WILEY, 2014. (THIS REFERENCE WILL BE REFFERRED TO AS TSAY MSTA.)
LÜTKEPOHL, HELMUT, NEW INTRODUCTION TO MULTIPLE TIME SERIES ANALYSIS, SPRINGER, 2006
HAMILTON, JAMES D., TIME SERIES ANALYSIS, PRINCETON UNIVERSITY PRESS, 1994
THE PRESENTATION INCLUDES FOUR ADDITIONAL MAJOR SECTIONS:
· SUMMARY OF SINGLE-VARIABLE UNIVARIATE TIME SERIES ANALYSIS
· SUMMARY OF MULTIVARIABLE UNIVARIATE TIME SERIES MODELS
· GENERAL MULTIVARIATE TIME SERIES ANALYSIS
· TIME SERIES ANALYSIS SOFTWARE
A DETAILED DESCRIPTION OF UNIVARIATE TIME SERIES MODELS IS PRESENTED IN THE TIMES TECHNICAL MANUAL, POSTED AT INTERNET WEBSITE http://www.foundationwebsite.org/TIMESVol1TechnicalBackground.pdf.
2. SUMMARY OF SINGLE-VARIABLE UNIVARIATE TIME SERIES ANALYSIS
THIS PRESENTATION BEGINS WITH A REVIEW OF CONCEPTS FROM SINGLE-VARIABLE UNIVARIATE TIME SERIES ANALYSIS (OR SCALAR TIME SERIES ANALYSIS). IN THIS SECTION, ATTENTION FOCUSES ON A SINGLE SCALAR RANDOM VARIABLE.
REFERENCES TREATING SINGLE-VARIABLE UNIVARIATE TIME SERIES INCLUDE:
BOX, GEORGE E. P., GWILYM M. JENKINS, GREGORY C. REINSEL AND GRETA M. LYUNG, TIME SERIES ANALYSIS, FORECASTING AND CONTROL, 5TH ED., WILEY, 2016
CRYER, JONATHAN D. AND KUNG-SIK CHAN, TIME SERIES ANALYSIS WITH APPLICATIONS IN R, 2ND ED., SPRINGER, 2008
MAJOR FEATURES OF TIME SERIES
A TIME SERIES IS A SET OF RANDOM VARIABLES HAVING A TIME INDEX: {X(t), tєT}, OR X1, X2,…,Xt.,,,. A TIME SERIES IS CALLED DISCRETE OR CONTINUOUS ACCORDING AS THE INDEX SET T IS DISCRETE OR CONTINUOUS. FOR THIS PRESENTATION, AND FOR MOST APPLICATIONS, THE TIME INDEX IS THE SET OF INTEGERS, 1, 2, …, AND THE TIMES TO WHICH THEY CORRESPOND ARE EQUALLY SPACED AND SUCCESSIVE IN TIME (E.G., HOURLY, DAILY, OR MONTHLY OBSERVATIONS OF A PHENOMENON OR PROCESS, SUCH AS TEMPERATURE OR STOCK PRICE).
IN GENERAL, THE RANDOM VARIABLE Xt MAY BE A VECTOR. IN THIS SECTION, IT IS A SINGLE-COMPONENT VECTOR, I.E., A SCALAR.
Figure: Example of a time series.
TIME SERIES DESCRIPTORS: MEAN, VARIANCE, COVARIANCE, ACF, PACF, SDF, STATIONARITY, HOMOGENEOUS NONSTATIONARITY, HETEROSCEDASTICITY
A STRICTLY STATIONARY
(OR STRONGLY STATIONARY) TIME SERIES (OR STOCHASTIC PROCESS) IS ONE FOR
WHICH THE JOINT DISTRIBUTION OF THE RANDOM VARIABLES ![]() IS THE SAME AS
THE DISTRIBUTION OF THE RANDOM VARIABLES
IS THE SAME AS
THE DISTRIBUTION OF THE RANDOM VARIABLES ![]() FOR ANY VALUE
OF k. LET US DENOTE THIS COMMON DISTRIBUTION AS F(X). FOR THIS PRESENTATION,
WE SHALL ASSUME THAT THE RANDOM VARIABLE IS CONTINUOUS, WITH DENSITY FUNCTION
f(X).
FOR ANY VALUE
OF k. LET US DENOTE THIS COMMON DISTRIBUTION AS F(X). FOR THIS PRESENTATION,
WE SHALL ASSUME THAT THE RANDOM VARIABLE IS CONTINUOUS, WITH DENSITY FUNCTION
f(X).
CONSIDERING THE CASE m = 1, THE DEFINITION OF STRICT STATIONARITY IMPLIES THAT THE MEAN OF THE TIME SERIES IS THE SAME FOR ALL VALUES OF t, AND THE VARIANCE IS ALSO THE SAME FOR ALL VALUES OF t.
CONSIDERING THE CASE m = 2, THE DEFINITION OF STRICT STATIONARITY IMPLIES THAT THE COVARIANCE OF ANY TWO RANDOM VARIABLES OF THE TIME INDEX SET, Xt AND Xt+k, IS THE SAME FOR ALL VALUES OF t.
FOR A STRICTLY STATIONARY SERIES, THE MEAN MAY BE ESTIMATED IN TWO WAYS: BY OBSERVING A SIMPLE RANDOM SAMPLE OF Xt AT A FIXED TIME t AND AVERAGING; OR BY OBSERVING A SAMPLE OF Xt FOR DIFFERENT TIMES t AND AVERAGING. IN REALITY, IT MAY BE IMPOSSIBLE OR IMPRACTICAL TO TAKE A SAMPLE AT A FIXED TIME. THESE TWO MEANS ARE CALLED THE TIME AVERAGE AND THE ENSEMBLE AVERAGE. FOR A STRICTLY STATIONARY TIME SERIES, THESE TWO AVERAGES ARE THE SAME. THIS PROPERTY IS CALLED ERGODICITY, AND THE TIME SERIES IS SAID TO BE ERGODIC. IN WHAT FOLLOWS, WE WILL ESTIMATE THE MEAN OF THE TIME SERIES (AND OTHER PROPERTIES, SUCH AS THE VARIANCE AND COVARIANCE) USING THE TIME AVERAGE.
AN OBSERVED TIME SERIES IS SAID TO BE A SINGLE REALIZATION OF AN UNDERLYING STOCHASTIC PROCESS (ABSTRACT OR REAL) THAT IS SAID TO GENERATE THE REALIZIATION. CONCEPTUALLY, THE UNDERLYING STOCHASTIC PROCESS COULD CONCEIVABLY GENERATE MANY ALTERNATIVE TIME SERIES, BUT IN MOST PRACTICAL APPLICATIONS ONLY ONE SERIES IS OBSERVED (SINCE TIME FLOWS AND WE MAY HAVE ONLY ONE CHANCE TO MAKE AN OBSERVATION AT A SPECIFIED TIME). THE UNDERLYING STOCHASTIC PROCESS IS ALSO CALLED THE DATA GENERATING PROCESS (DGP).
THE TERMS TIME SERIES AND STOCHASTIC PROCESS ARE USED SOMEWHAT INTERCHANGEABLY. THE TERM TIME SERIES IS USED MORE IN REFERRING TO A PARTICULAR OBSERVED REALIZATION OF A STOCHASTIC PROCESS, AND THE TERM STOCHASTIC PROCESS FOR THE THEORETICAL (UNREALIZED, MATHEMATICAL, CONCEPTUAL) MODEL THAT GENERATES THE REALIZATION.
NOTE THAT A SAMPLE OF OBSERVATIONS OVER TIME IS NOT, IN GENERAL, A SIMPLE RANDOM SAMPLE. THE MEMBERS OF A SAMPLE OF OBSERVATIONS FROM A REALIZATION OF A STOCHASTIC PROCESS ARE TYPICALLY CORRELATED. IF THEY ARE GENERATED BY AN UNDERLYING CONTINUOUS PROCESS, THE CORRELATION BETWEEN NEARBY OBSERVATIONS TYPICALLY INCREASES AS THE TIME DISTANCE BETWEEN THE OBSERVATIONS DECREASES. FOR THIS REASON, THE PRECISION OF A TIME AVERAGE TYPICALLY DIFFERS FROM THAT OF AN ENSEMBLE AVERAGE OF THE SAME SAMPLE SIZE.
STRICT STATIONARITY IS DIFFICULT TO ESTABLISH. A MORE USEFUL CONCEPT OF STATIONARITY IS WEAK STATIONARITY. A TIME SERIES IS WEAKLY STATIONARY IF THE MEAN AND VARIANCE ARE CONSTANT OVER TIME (I.E., THE MEAN AND VARIANCE OF Xt ARE CONSTANT FOR ALL VALUES OF THE INDEX t), AND THE COVARIANCE BETWEEN ANY TWO VARIABLE Xt AND Xt+k IS CONSTANT FOR A SPECIFIED VALUE OF k. (WEAK STATIONARITY IS ALSO CALLED SECOND-ORDER STATIONARITY OR COVARIANCE STATIONARITY.)
IN THIS PRESENTATION WE WILL BE WORKING WITH WEAK STATIONARITY, NOT STRICT STATIONARITY.
EXAMPLES:
Note: This version of the presentation does not include figures.
Figure: Example of stationary time series.
Figure: Example of a nonstationary time series exhibiting explosive behavior.
Figure: Example of nonseasonal homogeneous nonstationary time series.
Figure: Example of seasonal homogeneous nonstationary time series.
Figure: Example of heteroscedastic nonstationary time series.
THE MEAN OF A STATIONARY STOCHASTIC PROCESS IS:
![]()
THE VARIANCE IS:
![]()
AND THE AUTOCOVARIANCE AT LAG k IS:
![]()
THE AUTOCORRELATION AT LAG k IS:
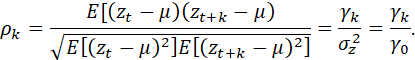
THE SEQUENCE OF AUTOCOVARIANCES FOR LAGS k = 1, 2, … IS CALLED THE AUTOCOVARIANCE FUNCTION, AND THE SEQUENCE OF AUTOCORRELATIONS FOR LAGS k = 1, 2,… IS CALLED THE AUTOCORRELATION FUNCTION. THE AUTOCORRELATION FUNCTION IS DENOTED AS ACF.
THE COSINE FOURIER TRANSFORM OF THE AUTOCOVARIANCE FUNCTION IS CALLED THE POWER SPECTRUM (OR SIMPLY, THE SPECTRUM).
![]()
THE POWER SPECTRUM IS A MEASURE OF THE DISTRIBUTION OF THE VARIANCE OF A TIME SERIES OVER A RANGE OF FREQUENCIES. (SEE BJRL FOR DISCUSSION.)
INTEGRATING THE PRECEDING FUNCTION OVER ITS RANGE, WE OBTAIN:
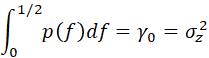
THE POWER SPECTRUM CONTAINS ALL OF THE INFORMATION IN THE AUTOCOVARIANCE FUNCTION; EITHER ONE MAY BE CONSTRUCTED FROM THE OTHER. THE POWER SPECTRUM IS OF DIRECT INTEREST IN PHYSICAL APPLICATIONS INVOLVING DETERMINISTIC FREQUENCIES, BUT ALSO OF INTEREST FOR TESTING THE ADEQUACY OF TENTATIVE MODELS IN GENERAL.
THE FORMULA FOR THE AUTOCOVARIANCE FUNCTION IN TERMS OF THE POWER SPRECTRUM IS:

THE SPECTRAL DENSITY FUNCTION IS THE POWER SPECTRUM NORMALIZED BY DIVIDING BY THE VARIANCE:
![]()
THE SPECTRAL DENSITY FUNCTION HAS THE SAME PROPERTIES AS AN ORDINARY PROBABILITY DENSITY FUNCTION, I.E., IT IS POSITIVE AND INTEGRATES TO ONE.
LET x = (x1,…,xn)’ DENOTE A SEQUENCE OF n OBSERVATIONS FROM A TIME SERIES REALIZATION (OBSERVATION) OF A STOCHASTIC PROCESS, WHERE n DENOTES THE NUMBER OF TIME POINTS IN THE OBSERVED SEQUENCE.
(IN THIS PRESENTATION WE SHALL USUALLY DENOTE ROW VECTORS, SUCH AS A SEQUENCE OF OBSERVED VALUES OF A TIME SERIES, USING PRIMED BOLD-FACE LETTERS. IN GENERAL, ABSTRACT (CONCEPTUAL, THEORETICAL) RANDOM VARIABLES WILL BE DENOTED BY UPPER-CASE LETTERS AND REALIZED VALUES BY LOWER-CASE LETTERS. THIS PRACTICE IS NOT UNIVERSAL, HOWEVER, AND WE MAY DEPART FROM IT IN ORDER TO FOLLOW THE NOTATION OF A CITED AUTHOR (AND REPRESENT ABSTRACT RANDOM VARIABLES IN EITHER UPPOR OR LOWER CASE). VECTORS ARE SHOWN IN BOLDFACE FONT. MATRICES ARE SHOWN IN NON-BOLDFACE FONT. (THIS LAST CONVENTION IS NOT STANDARD, AND WILL BE CHANGED IN A SUBSEQUENT VERSION.)
THE SAMPLE ESTIMATES OF THE MEAN, VARIANCE AND AUTOCOVARIANCE AT LAG k ARE:
![]()
![]()
AND
![]()
NOTE THAT IT IS CUSTOMARY
IN TIME SERIES ANALYSIS TO USE A DIVISOR n INSTEAD OF n-1 IN THE EXPRESSION ![]() FOR THE ESTIMATED MEAN. IF THE DIVISOR n-1 IS USED,
THE SYMBOL
FOR THE ESTIMATED MEAN. IF THE DIVISOR n-1 IS USED,
THE SYMBOL ![]() IS USED.
IS USED.
THE AUTOCORRELATION AT LAG k IS ESTIMATED AS:
![]()
AUTOCOVARIANCE AND AUTOCORRELATION MATRICES MAY BE FORMED FOR THE VARIATES COMPRISING A TIME SERIES, BUT, FOR A STATIONARY SERIES, THEY ARE HIGHLY REDUNDANT, SINCE ALL ENTRIES ALONG ANY DIAGONAL PARALLELLING THE TOP-LEFT TO LOWER-RIGHT PRINCIPAL DIAGONAL ARE IDENTICAL. FOR THIS REASON, FOR UNIVARIATE TIME SERIES, ATTENTION FOCUSES ON THE AUTOCOVARIANCE FUNCTION AND AUTOCORRELATION FUNCTION, NOT ON THE FULL AUTOCOVARIANCE AND AUTOCORRELATION MATRICES FOR A LONG TIME SERIES. AUTOCOVARIANCE AND AUTOCORRELATION MATRICES ARE OF INTEREST, HOWEVER, FOR SHORT SERIES. THE AUTOCORRELATION FUNCTION IS SIMPLY THE LIST OF ENTRIES ALONG THE DIAGONAL (OF THE AUTOCORRELATION MATRIX) GOING FROM UPPER RIGHT TO LOWER LEFT.
THE SAMPLE ESTIMATES OF THE POWER SPECTRUM AND SPECTRAL DENSITY FUNCTION OBTAINED BY INSERTING SAMPLE ESTIMATES FOR AUTOCOVARIANCES OR AUTOCORRELATIONS ARE POOR (INCONSISTENT AND OF HIGH VARIANCE). THE REASON FOR THIS IS THAT THE ESTIMATES OF AUTOCOVARIANCES AND AUTOCORRELATIONS AT HIGH LAGS ARE BASED ON A SMALL SAMPLE SIZES, AND THEIR VARIANCES REMAIN HIGH EVEN AS THE TOTAL SAMPLE SIZE INCREASES.
USEFUL ESTIMATES ARE OBTAINED BY WEIGHTING TO DIMINISH THE CONTRIBUTION TO THE ESTIMATE FROM LOWER FREQUENCIES (I.E., FROM LONG LAGS, FOR WHICH THE AUTOCOVARIANCE AND AUTOCORRELATION ESTIMATES ARE BASED ON FEW OBSERVATIONS). A SMOOTHED ESTIMATE OF THE POWER SPECTRUM IS:
![]()
WHERE THE λk ARE WEIGHTS CALLED A LAG WINDOW.
THIS PRESENTATION PRESENTS VERY LITTLE MATERIAL ON THE TIME SERIES ANALYSIS IN THE FREQUENCY DOMAIN. REFERENCES ON THIS TOPIC INCLUDE THE FOLLOWING:
1. Jenkins, Gwilym M. and Donald G. Watts, Spectral Analysis and its applications, Holden-Day, 1968
2. Priestley, M. B., Spectral Analysis and Time Series, Academic Press, 1981
3. Harris, Bernard, ed., Spectral Analysis of Time Series, Wiley, 1967
THE PARTIAL AUTOCORRELATION COEFFICIENT IS DEFINED AS THE k-th COEFFICIENT, Økk, OF AN AUTOREGRESSIVE REPRESENTATION OF ORDER k. CONSIDERED AS A FUNCTION OF k, THIS QUANTITY IS CALLED THE PARTIAL AUTOCORRELATION FUNCTION (PACF), UNLIKE THE ACF, THE PACF DOES NOT CHARACTERIZE A STOCHASTIC PROCESS. IT IS A DIAGNOSTIC TOOL USED TO HELP IDENTIFY THE ORDER OF A STOCHATIC PROCESS. FOR AN AR(p) PROCESS THE PACF WILL BE NONZERO FOR k <=p AND ZERO FOR k > p.
FOR AN AR(p) PROCESS, THE ACF WILL DIE OFF, I.E., TEND TO DECREASE AS THE LAG INCREASES. FOR A MA(q) PROCESS, THE ACF WILL CUT OFF AT THE ORDER, q, OF THE PROCESS. IN CONTRAST, FOR AN AR(p) PROCESS THE PACF WILL CUT OFF AT THE ORDER, p, OF THE PROCESS, AND FOR AN MA(q) PROCESS THE PACF WILL DIE OFF. THE ACF AND PACF ARE HENCE USEFUL TOOLS IN ASSESSING CANDIDATE ORDERS FOR AR AND MA MODELS. FOR ARMA PROCESSES, THE ACF AND PACF WILL TEND TO DIE OFF AFTER A CERTAIN LAG.
THEORETICAL MODELS: WHITE NOISE, AUTOREGRESSIVE, MOVING AVERAGE, ARMA, ARIMA, SEASONAL
THERE ARE A NUMBER OF TYPES OF STOCHASTIC PROCESS MODELS, OR TIME SERIES MODELS, THAT ARE HIGHLY USEFUL FOR REPRESENTING REAL-WORLD PHENOMENA. SOME OF THEM ARE STATIONARY, AND SOME ARE A PARTICULAR TYPE OF NONSTATIONARY, CALLED HOMOGENEOUS NONSTATIONARY. THESE MODELS WILL NOW BE DESCRIBED.
EXAMPLES OF EACH MODEL WILL BE PRESENTED. THE MODEL WILL BE REPRESENTED BY THE MODEL EQUATION, A SAMPLE TIME SERIES, THE ACF, THE PACF AND THE SPECTRAL DENSITY FUNCTION.
IN GENERAL, A STOCHASTIC PROCESS MAY BE REPRESENTED BY THE JOINT PROBABILITY DISTRIBUTION FUNCTION OR THE MODEL. SINCE A NORMAL PROCESS (I.E., ONE IN WHICH THE MODEL ERROR TERMS ARE NORMALLY DISTRIBUTED) IS CHARACTERIZED (DEFINED, COMPLETELY SPECIFIED) BY ITS MEAN, VARIANCES AND COVARIANCES, A NORMAL PROCESS MAY BE REPRESENTED BY ITS MEAN, VARIANCE AND AUTOCOVARIANCE FUNCTION (OR POWER SPECTRUM). IN WHAT FOLLOWS, WE WILL ASSUME THAT THE MODEL RESIDUALS HAVE MEAN ZERO AND CONSTANT VARIANCE σ2. IN THIS CASE, A NORMAL PROCESS IS CHARACTERIZED BY THE ACF OR SPECTRAL DENSITY FUNCTION (IN ADDITION TO THE VARIANCE, σ2).
STATIONARY PROCESSES
WHITE NOISE PROCESS
A WHITE NOISE
PROCESS IS A SEQUENCE OF INDEPENDENT AND IDENTICALLY DISTRIBUTED RANDOM
VARIABLES. IT IS USUALLY DENOTED AS A SEQUENCE a1, a2,
…, at ,…. IT IS USUALLY ASSUMED TO HAVE MEAN ZERO. THE VARIANCE IS
DENOTED BY ![]()
MODEL:
![]()
Figures: Sample time series, ACF, PACF, SDF.
IN THE FOLLOWING, WE SHALL USE THE SYMBOL at TO DENOTE A WHITE NOISE PROCESS (I.E., A SEQUENCE OF UNCORRELATED RANDOM VARIABLES WITH MEAN ZERO AND VARIANCE σ2).
MOVING AVERAGE (MA) PROCESS
GENERAL MODEL:
![]()
WHERE
![]()
IN ORDER FOR THIS MODEL TO REPRESENT REALISTIC PROCESSES, IT IS NECESSARY TO RESTRICT THE MODEL SUCH THAT THE ROOTS OF THE EQUATION
![]()
ARE LOCATED OUTSIDE THE UNIT CIRCLE. THIS CONDITION IS CALLED THE INVERTIBILITY PROPERTY. FOR INVERTIBLE PROCESSES, THE INFLUENCE OF PAST OBSERVATIONS TENDS TO DIMINISH AS THE TIME INTERVAL INCREASES.
SAMPLE MODEL:
![]()
OR
![]()
Figures: Sample time series, ACF, PACF, SDF.
AUTOREGRESSIVE (AR) PROCESS
GENERAL MODEL:
![]()
OR
![]()
OR
![]()
OR
![]()
WHERE
![]()
IN ORDER FOR THE PROCESS TO BE STATIONARY, IT IS NECESSARY THAT ALL ROOTS OF THE EQUATION
![]()
ARE LOCATED OUTSIDE THE UNIT CIRCLE.
SAMPLE MODEL:
![]()
OR
![]()
Figures: Sample time series, ACF, PACF, SDF.
AUTOREGRESSIVE MOVING AVERAGE (ARMA) PROCESS
THE AUTOREGRESSIVE AND MOVING AVERAGE PROCESSES MAY BE COMBINED, INTO WHAT IS CALLED AN AUTOREGRESSIVE – MOVING AVERAGE PROCESS.
GENERAL MODEL:
![]()
OR
![]()
OR
![]()
OR
![]()
WHERE
![]()
AND
![]()
SAMPLE MODEL:
![]()
OR
![]()
Figures: Sample time series, ACF, PACF, SDF.
SEASONAL PROCESS
SUPPOSE THAT OBSERVATIONS OCCURRING AT AN INTERVAL OF s TIME UNITS APART ARE RELATED. FOR EXAMPLE, MONTHLY SALES OF A PRODUCT MAY FOLLOW AN ANNUAL PATTERN IN WHICH OBSERVATIONS 12 MONTHS APART ARE CORRELATED. A USEFUL MODEL IN THIS SITUATION IS A MULTIPLICATIVE SEASONAL MODEL.
GENERAL MODEL (MULTIPLICATIVE SEASONAL ARMA MODEL):
![]()
WHERE THE PERIOD OF THE SEASON IS s, THE INTERVAL-s BACKSHIFT OPERATOR IS DEFINED BY
![]()
![]()
AND
![]()
AS IN THE CASE OF NONSEASONAL MODELS, IT IS REQUIRED THAT THE ROOTS OF THE ΦP AND ΘQ POLYNOMIALS BE LOCATED OUTSIDE THE UNIT CIRCLE.
SAMPLE MODEL:
![]()
OR
![]()
Figures: Sample time series, ACF, PACF, SDF.
HOMOGENEOUS NONSTATIONARY PROCESS
THE MODELS DESCRIBED ABOVE, IN WHICH THE ROOTS OF THE PHI POLYNOMIALS ARE OUTSIDE THE UNIT CIRCLE, REPRESENT STATIONARY PROCESSES. IF IT IS ALLOWED FOR THE ROOTS OF THE PHI POLYNOMIALS TO BE ON THE UNIT CIRCLE, THE PROCESS IS NONSTATIONARY, BUT IN A PARTICULAR WAY. THE LEVEL OF THE PROCESS MAY WANDER, BUT EXPLOSIVE BEHAVIOR DOES NOT OCCUR.
IF THE ROOTS OF THE PHI POLYNOMIALS ARE IMAGINARY, THE PROCESS WILL EXHIBIT RANDOM PERIODIC BEHAVIOR THAT APPEARS SINUSOIDAL IN NATURE. IF THE ROOTS ARE REAL, THE PROCESS LEVEL WANDERS. PERIODIC BEHAVIOR MAY BE PRESENT, BUT IT IS NOT SINUSOIDAL IN NATURE.
THE TYPE OF NONSTATIONARY
BEHAVIOR EXHIBITED BY SERIES HAVING ROOTS ON THE UNIT CIRCLE IS CALLED HOMOGENEOUS
NONSTATIONARY BEHAVIOR. THE MOST WIDELY USED MODELS OF THIS SORT ARE ONES
IN WHICH THE PHI POLYNOMIAL HAS FACTORS OF THE FORM ![]() = (1 – B) OR
= (1 – B) OR ![]() = (1 – Bs)
(THAT IS, THE ROOTS ARE REAL). THESE MODELS HAVE THE FORM
= (1 – Bs)
(THAT IS, THE ROOTS ARE REAL). THESE MODELS HAVE THE FORM
![]()
IN MOST APPLICATIONS, THERE ARE ONLY ONE OR TWO PHI PARAMETERS IN EACH PHI POLYNOMIAL, ONE OR TWO THETA PARAMETERS IN EACH THETA PARAMETER, AND THE VALUES OF d AND D ARE USUALLY ZERO OR ONE.
NOTATION: THE PRECEDING MODEL IS REFERRED TO AS A BOX-JENKINS
MODEL WITH PARAMETERS (p,d,q) x (P,D,Q)s (OR OF ORDER (p,d,q)
x (P,D,Q)s). SOME AUTHORS USE THE SYMBOL Δ TO DENOTE THE
FIRST DIFFERENCE (1 – B) INSTEAD OF ![]() . IN ECONOMETRICS, IT IS STANDARD PRACTICE TO USE L
TO DENOTE THE BACKSHIFT OPERATOR (INSTEAD OF B).
. IN ECONOMETRICS, IT IS STANDARD PRACTICE TO USE L
TO DENOTE THE BACKSHIFT OPERATOR (INSTEAD OF B).
A MODEL HAVING THE
DIFFERENCE TERMS (![]() TERMS) IS CALLED AN INTEGRATED PROCESS. A
MODEL HAVING AN AUTOREGRESSIVE (PHI) POLYNOMIAL, DIFFERENCE TERMS, AND A MOVING
AVERAGE (THETA) POLYNOMIAL IS CALLED AN AUTOREGRESSIVE INTEGRATED MOVING
AVERAGE (ARIMA) PROCESS.
TERMS) IS CALLED AN INTEGRATED PROCESS. A
MODEL HAVING AN AUTOREGRESSIVE (PHI) POLYNOMIAL, DIFFERENCE TERMS, AND A MOVING
AVERAGE (THETA) POLYNOMIAL IS CALLED AN AUTOREGRESSIVE INTEGRATED MOVING
AVERAGE (ARIMA) PROCESS.
EXAMPLE:
![]()
OR
![]()
Figures: Sample time series.
EXAMPLE:
![]()
OR
![]()
Figures: Sample time series.
EXAMPLE:
![]()
OR
![]()
Figures: Sample time series.
ALTHOUGH DIFFERENCING IS A WIDELY USED METHOD FOR TRANSFORMING TO ACHIEVE STATIONARITY, IT IS APPROPRIATE ONLY IF THE UNDERLYING STOCHASTIC PROCESS IS REASONABLY REPRESENTED BY AN ARIMA MODEL HAVING A REAL UNIT ROOT. FOR A SERIES THAT FLUCTUATES AROUND A DETERMINISTIC TREND, APPLYING THIS TRANSFORMATION TO ACHIEVE STATIONARITY WOULD BE A MISTAKE. DIFFERENCING WOULD IN FACT REMOVE THE TREND, BUT IT WOULD BE AN INCORRECT SPECIFICATION, AND WOULD IN FACT INTRODUCE A UNIT ROOT INTO THE TRANSFORMED DATA. A FORECASTING MODEL BASED ON THIS MODEL WOULD PRODUCE REASONABLE LEAD-ONE FORECASTS, BUT THE FORECASTS BEYOND THAT POINT WOULD HAVE MUCH LARGER ERROR VARIANCES THAN FORECASTS BASED ON THE CORRECT MODEL.
Figure: Deterministic trend plus white noise series.
IMPULSE RESPONSE FUNCTION (IRF)
AS MENTIONED, FOR A (WEAKLY)
STATIONARY PROCESS, THE ROOTS OF THE PHI AND THETA POLNOMIALS ARE OUTSIDE THE UNIT
CIRCLE. IN THIS CASE, THE LINEAR OPERATOR ![]() (B) MAY BE INVERTED, AND THE ARMA MODEL
(B) MAY BE INVERTED, AND THE ARMA MODEL
![]()
MAY BE WRITTEN AS
![]()
WHERE
![]()
THIS REPRESENTATION IS CALLED A WOLD DECOMPOSITION, AND THE SERIES Ψ1, Ψ2,… IS CALLED THE IMPULSE RESPONSE FUNCTION (IRF). THE Ψ SERIES IS FINITE FOR A PURE MOVING AVERAGE PROCESS, AND INFINITE FOR AN AUTOREGRESSIVE MODEL (EITHER AR OR ARMA).
THE FUNCTION Ψk SHOWS THE AVERAGE EFFECT OF A UNIT INCREASE IN THE MODEL INPUT at, ON THE MODEL OUTPUT, zt+k. NOTE THAT THE IMPULSE RESPONSE FUNCTION REPRESENTS THE EFFECT OF A UNIT CHANGE IN THE INPUT (at) WITH THE PROCESS FUNCTIONING AS SPECIFIED BY A CAUSAL MODEL OF THE STOCHASTIC PROCESS UNDERLYING THE MODEL. IT REPRESENTS THE EFFECT OF AN OBSERVED UNIT CHANGE IN THE INPUT IF THE MODEL ERROR TERMS OF UNDERLYING PROCESS REPRESENT OBSERVED CHANGES; IT REPRESENTS AN ESTIMATE OF THE EFFECT OF A FORCED CHANGE IN THE INPUT IF THE MODEL ERROR TERMS OF THE UNDERLYING MODEL REPRESENT FORCED CHANGES.
WHILE THE IMPULSE RESPONSE FUNCTION CHARACTERIZES A TIME SERIES, IT IS NOT USED A LOT IN ANALYSIS OF UNIVARIATE TIME SERIES MODELS THAT INCLUDE NO EXPLANATORY VARIABLES, IN WHICH CASE IT INDICATES THE RESPONSE TO CHANGES IN THE MODEL ERROR TERMS. IT IS USED MORE IN ANALYSIS OF MODELS CONTAINING EXPLANATORY VARIABLES, TO SHOW THE RESPONSE (OF AN OUTPUT VARIABLE) TO CHANGES IN THEM.
THE SUM OF ALL OF THE IMPULSE RESPONSES, WHICH IS THE TOTAL EFFECT OF A UNIT INCREASE ON ALL FUTURE OUTPUTS,
![]()
IS CALLED THE TOTAL MULTIPLIERS OR LONG-RUN EFFECTS. THE SUM OF THE IMPULSE RESPONSES UP TO A VALUE n
![]()
IS CALLED THE ACCUMULATED RESPONSE OVER n PERIODS, OR THE n-th INTERIM MULTIPLIERS.
ANALYSIS OF THE IMPULSE RESPONSE FUNCTION IS REFERRED TO AS MULTIPLIER ANALYSIS IN ECONOMICS.
THE PRECEDING DISCUSSION CONSIDERS THE IMPULSE RESPONSE FUNCTION FOR A STATIONARY PROCESS. THE DEFINITION OF THE IMPULSE RESPONSE FUNCTION IS THE SAME FOR HOMOGENEOUS NONSTATIONARY PROCESSES, BUT THE PROCESS CANNOT BE REPRESENTED AS A CONVERGENT SERIES, AS SHOWN ABOVE. FORMULAS FOR THE IMPULSE RESPONSE FUNCTION (I.E., THE Ψ’s) IN THE HOMOGENEOUS NONSTATIONARY CASE WILL BE PRESENTED LATER.
STATIONARITY TRANSFORMATIONS, TESTS OF HYPOTHESES
THE PRECEDING MODELS – THE CLASS OF AUTOREGRESSIVE INTEGRATED MOVING AVERAGE MODELS – CAN REPRESENT A WIDE RANGE OF PHENOMENA, AND THE MODELS MAY BE EITHER STATIONARY OR NONSTATIONARY. IN ORDER TO USE ONE OF THESE MODELS IN A PARTICULAR APPLICATION, IT MUST BE DEMONSTRATED THAT THE OBSERVED TIME SERIES CAN REASONABLY BE REPRESENTED BY A MEMBER OF THIS CLASS.
AN ARIMA MODEL IS APPROPRATE IF THE OBSERVED DATA SERIES CAN BE DEMONSTRATED TO BE STATIONARY, OR IF IT CAN BE CONVERTED TO A STATIONARY TIME SERIES BY DIFFERENCING (OR, MORE GENERALLY, BY TRANSFORMING USING ANY POLYNOMIAL FILTER FOR WHICH THE ROOTS ARE ON THE UNIT CIRCLE).
A STANDARD PROCEDURE FOR TRANSFORMING A NONSTATIONARY STOCHASTIC PROCESS TO A STATIONARY ONE IS DIFFERENCING. DIFFERENCING IS APPROPRIATE IF THE OBSERVED SERIES EXHIBITS HOMOGENEOUS NONSTATIONARY BEHAVIOR OR SEASONALITY. SUCH BEHAVIOR IS EASILY RECOGNIZED BY VISUAL INSPECTION.
A STATISTICAL TEST OF THE HYPOTHESIS THAT A PROCESS IS NONSTATIONARY VS. THE ALTERNATIVE THAT IT IS STATIONARY IS THE DICKEY-FULLER TEST. (SEE ECONOMETRIC ANALYSIS 7th ED. BY WILLIAM H. GREENE (PEARSON EDUCATION / PRENTICE HALL, 2012) FOR DISCUSSION.) THE DICKEY-FULLER TEST IS A LITTLE COMPLICATED, SINCE THE SAMPLING DISTRIBUTION OF THE TEST STATISTIC DEPENDS ON THE NATURE OF THE NONSTATIONARITY (I.E., ON THE TRUE PROCESS). THERE IS NOT JUST ONE DICKEY-FULLER TEST, BUT A NUMBER OF THEM, FOR DIFFERENT SITUATIONS (E.G., AN APPARENT RANDOM WALK, OR A RANDOM WALK WITH DRIFT, OR A RANDOM WALK WITH TREND). (THE SAMPLING DISTRIBUTION IS NOT AVAILABLE IN CLOSED FORM, EVEN FOR SIMPLE HOMOGENEOUS NONSTATIONARY PROCESSES SUCH AS RANDOM WALKS.) FOR SHORT TIME SERIES, THE TESTS ARE NOT RELIABLE.
A STATISTICAL TEST OF THE HYPOTHESIS OF NONSTATIONARITY (OR STATIONARITY) IS CALLED A “UNIT ROOT” TEST, SINCE IT IS A TEST OF WHETHER THE AUTOREGRESSIVE POLYNOMIAL OF AN AUTOREGRESSIVE PROCESS HAS A ROOT ON (OR OUTSIDE) THE UNIT CIRCLE.
IN ECONOMETRIC APPLICATIONS, MUCH ATTENTION HAS BEEN FOCUSED ON WHETHER DIFFERENCING IS REQUIRED TO ACHIEVE STATIONARITY, VS. THE USE OF A MODEL THAT HAS A ROOT OF THE AUTOREGRESSIVE POLYNOMIAL JUST OUTSIDE THE UNIT CIRCLE, E.G., (1 – B) VS. (1 - .95B). IT SHOULD BE NOTED THAT THE BOX-JENKINS (ARIMA) MODELS ARE USED PRIMARILY IN SHORT-TERM FORECASTING, AND WHICH OF THESE REPRESENTATIONS IS SELECTED WILL MAKE LITTLE DIFFERENCE IN THE ACCURACY OF SHORT-TERM FORECASTS. THE LONG-TERM BEHAVIOR OF THESE MODEL ALTERNATIVES IS SUBSTANTIALLY DIFFERENT, HOWEVER, SINCE THE EFFECT OF A SHOCK AT A PARTICULAR TIME DIES OUT WITH THE LATTER MODEL (1 - .95B) BUT NOT THE FORMER MODEL (1 – B). FOR SHORT TIME SERIES, THE POWER OF THE DICKEY-FULLER TEST TO DISCRIMINATE BETWEEN THESE TWO MODEL CHOICES WILL BE LOW. TO CREDIBLY MAKE SUCH AN ASSESSMENT WOULD REQUIRE A QUITE LONG TIME SERIES.
IN PRACTICE, ONLY ONE OR TWO DIFFERENCES IS NECESSARY TO ACHIEVE STATIONARITY FOR A NONSTATIONARY SERIES. FOR SEASONAL SERIES, IT IS USUAL TO SEE A DIFFERENCE OF INTERVAL ONE AND INTERVAL s, WHERE s DENOTES THE NUMBER OF TIME INTERVALS BETWEEN RECURRING SEASONS.
MODEL SPECIFICATION; ESTIMATION OF PARAMETERS (METHOD OF MOMENTS, LEAST-SQUARES, MAXIMUM LIKELIHOOD, BAYESIAN); NONLINEAR ESTIMATION
AFTER IT HAS BEEN ESTABLISHED THAT THE DATA GENERATING PROCESS IS STATIONARY, OR DIFFERENCING HAS BEEN APPLIED TO TRANSFORM THE PROCESS TO A STATIONARY ONE, WORK MAY PROCEED ON MODEL SPECIFICATION AND ESTIMATION OF MODEL PARAMETERS.
THE FIRST STEP IS TO ESTIMATE VALUES OF THE STRUCTURAL PARAMETERS, p, d, q, s, P, D, Q. THIS IS DONE BY EXAMINING THE AUTOCORRELATION FUNCTION AND PARTIAL AUTOCORRELATION FUNCTION. THE VALUES FOR s, d AND d WILL HAVE BEEN DETERMINED DURING THE COURSE OF DECIDING WHETHER AND HOW DIFFERENCING SHOULD BE APPLIED TO TRANSFORM A NONSTATIONARY SERIES TO A STATIONARY ONE. WHAT REMAINS IS TO DETERMINE REASONABLE VALUES FOR p, q, P AND Q.
AS EXHIBITED IN THE FIGURES PRESENTED EARLIER, THE AUTOCORRELATION FUNCTION CUTS OFF FOR A PURE MOVING AVERAGE PROCESS, AND TAILS OFF FOR A PURE AUTOREGRESSIVE PROCESS. THE PARTIAL AUTOCORRELATION FUNCTION CUTS OFF FOR A PURE AUTOREGRESSIVE PROCESS AND TAILS OFF FOR A PURE MOVING AVERAGE PROCESS. FOR MIXED PROCESSES, THE BEHAVIOR IS MORE COMPLICATED. REFERENCE BJRL PRESENTS TABLES THAT MAY BE USED AS GUIDES TO INFER TENTATIVE VALUES FOR p, q, P AND Q (FOR ARBITRARY s).
NOTE THAT THE MODELS DESCRIBED HERE ARE NOT THE FULL RANGE OF MODELS THAT MAY BE CONSIDERED. SOME MODELS MAY CONTAIN MEANS AND TIME TRENDS. (A MEAN MAY BE REMOVED BY SINGLE DIFFERENCING, AND A TREND BY DOUBLE DIFFERENCING, BUT SUCH TRANSFORMATIONS ARE NOT RECOMMENDED FOR SERIES HAVING A CONSTANT MEAN OR LINEAR TREND, SINCE DIFFERENCING IN THIS CASE WILL INTRODUCE A UNIT ROOT INTO THE MODEL ERROR TERM, CAUSING THE MODEL TO BE NON-INVERTIBLE.)
FOR A SPECIFIED MODEL STRUCTURE (VALUES OF p, d, q, s, P, D, Q), THE MODEL PARAMETERS (PHIs AND THETAs) MAY BE ESTIMATED IN A NUMBER OF WAYS. THE STANDARD ESTIMATION PROCEDURES ARE THE FOLLOWING. NOTE THAT PRIOR TO ESTIMATION, ADDITIONAL TRANSFORMATIONS MAY BE APPLIED TO THE DATA (E.G., A LOGARITHMIC TRANSFORMATION, IF THE STANDARD DEVIATION OF THE OBSERVATIONS APPEARS TO VARY ACCORDING TO THE LEVEL OF THE SERIES, IN ORDER TO ACHIEVE A CONSTANT VARIANCE FOR THE MODEL RESIDUALS).
METHOD OF MOMENTS
FROM THE AVAILABLE SAMPLE DATA (TRANSFORMED TO STATIONARY), THE FIRST AND SECOND-ORDER SAMPLE MOMENTS (MEANS, VARIANCE, COVARIANCES) ARE CALCULATED. FOR AN ASSUMED MODEL STRUCTURE (VALUES OF p,q,s,P,Q), THE CORRESPONDING POPULATION MOMENTS ARE DETERMINED, ASSUMING AN UNDERLYING PROBABILITY DISTRIBUTION FOR THE MODEL ERROR TERM (SUCH AS NORMALITY). THE POPULATION MOMENTS ARE FUNCTIONS OF THE MODEL PARAMETERS (PHIs AND THETAs). THE POPULATION VALUES OF THE MOMENTS ARE SET EQUAL TO THE SAMPLE VALUES, AND THE EQUATIONS SOLVED FOR THE MODEL PARAMETERS.
METHOD OF LEAST SQUARES
THE PARAMETER ESTIMATES ARE THE VALUES THAT MINIMIZE THE RESIDUAL SUM OF SQUARES. THE COMPUTATIONAL PROCEDURES FOR MINIMIZING THE RESIDUAL SUM OF SQUARES IS SOMEWHAT COMPLICATED. IT IS DESCRIBED IN DETAIL IN THE TIMES TECHNICAL MANUAL AND IN THE BJRL BOOK.
THE METHOD OF LEAST SQUARES IS VERY BASIC, IN THAT IT IS A PROCEDURE THAT MAY BE IMPLEMENTED WITHOUT ANY CONSIDERATION OF AN UNDERLYING PROBABILITY DISTRIBUTION.
TO IMPLEMENT THE LEAST-SQUARES METHOD FOR A MODEL THAT INCLUDES MOVING-AVERAGE TERMS, VALUES MUST BE SPECIFIED FOR THE q MODEL ERROR TERMS PRECEDING THE START OF THE SAMPLE SERIES. THERE ARE TWO APPROACHES TO THE LEAST-SQUARES METHOD, CORRESPONDING TO HOW THIS IS DONE. FOR CONDITIONAL LEAST-SQUARES ESTIMATES, THE INITIAL VALUES OF THE MODEL ERROR TERMS ARE ASSUMED TO BE EQUAL TO ZERO. FOR UNCONDITIONAL LEAST-SQUARES ESTIMATES, THE INITIAL VALUES ARE ESTIMATED AS MODEL PARAMETERS. THE CONDITIONAL APPROACH IS USED BECAUSE IT IS SIMPLER TO IMPLEMENT (E.G., CLOSED-FORM SOLUTIONS MAY BE AVAILABLE FOR THE CONDITIONAL METHOD). FOR A LONG SAMPLE TIME SERIES, THE TWO METHODS PRODUCE SIMILAR RESULTS. THE DIFFERENCE IN THE METHODS IS MOST PRONOUNCED FOR MOVING-AVERAGE PARAMETER VALUES NEAR THE UNIT CIRCLE (WHERE THE EFFECT OF MODEL ERROR TERMS PERSISTS FOR A LONGER TIME, SO THAT THE EFFECT OF THE ASSUMED VALUES OF ZERO PERSISTS FOR A LONGER TIME).
MAXIMUM LIKELIHOOD
THE PARAMETER VALUES ARE THOSE THAT MAXIMIZE THE LIKELIHOOD, ASSUMING A NORMAL DISTRIBUTION (OR OTHER SUITABLE DISTRIBUTION) FOR THE MODEL ERROR TERMS.
THE ESTIMATES PRODUCED BY THE METHOD OF LEAST SQUARES PRODUCES THE SAME ESTIMATES AS THE METHOD OF MAXIMUM LIKELIHOOD FOR A NORMAL DISTRIBUTION.
AS IN THE CASE OF LEAST-SQUARES ESTIMATION, THE PARAMETER ESTIMATION MAY BE IMPLEMENTED CONDITIONAL ON SPECIFIED VALUES (ZEROS) FOR THE INITIAL VALUES OF THE MODEL ERROR TERMS, OR UNCONDITIONALLY.
BAYESIAN ESTIMATES
A PRIOR DISTRIBUTION IS SPECIFIED FOR THE MODEL PARAMETERS, AND A SAMPLING DISTRIBUTION GIVEN THE MODEL PARAMETERS. THE POSTERIOR DISTRIBUTION OF THE MODEL PARAMETERS IS DETERMINED, GIVEN THE OBSERVED SAMPLE (OF STATIONARY-TRANSFORMED DATA). THE PARAMETER ESTIMATES ARE THEIR EXPECTED VALUES, GIVEN THE POSTERIOR DISTRIBUTION.
THIS PRESENTATION WILL NOT DESCRIBE BAYESIAN ESTIMATION. REFERENCES ON THIS TOPIC INCLUDE:
GELMAN, ANDREW, JOHN B. CARLIN, HAL S. STERN, DAVID B. DUNSON, AKI VEHTARI AND DONALD B. RUBIN, BAYESIAN DATA ANAYSIS, 3RD ED., CRC PRESS, 2014
ROSSI, PETER E., GREG M. ALLENBY AND ROBERT MCCOLLUCH, BAYESIAN STATISTICS AND MARKETING, WILEY, 2005
BOX, GEORGE E. P. AND GEORGE C. TIAO, BAYESIAN INFERENCE IN STATISTICAL ANALYSIS, WILEY, 1973
CARLIN, BRADLEY P. AND THOMAS A. LOUIS, BAYES AND EMPIRICAL BAYES METHODS FOR DATA ANALYSIS, 2ND ED., CHAPMAN & HALL / CRC, 2000
LINEAR STATISTICAL MODELS VS. NONLINEAR STATISTICAL MODELS
IMPLEMENTATION OF THE PRECEDING METHODS OF ESTIMATION IS SOMEWHAT COMPLICATED, AND NUMERICAL METHODS ARE REQUIRED TO IMPLEMENT THEM IN MANY CASES. FOR PURE AUTOREGRESSIVE MODELS, THE MODELS ARE LINEAR STATISTICAL MODELS, AND THE ESTIMATION MAY PROCEED IN THE USUAL FASHION. FOR MODELS INVOLVING MOVING AVERAGE TERMS, THE MODELS ARE NOT LINEAR IN THE PARAMETERS, AND NUMERICAL METHODS MUST BE USED TO DETERMINE THE ESTIMATES.
FOR MODELS INVOLVING A SMALL NUMBER OF PARAMETERS (E.G., AN ARMA MODEL HAVING p + q < 2) THE SIMPLEST APPROACH TO PARAMETER ESTIMATION IS TO ESTIMATE THE LIKELIHOOD SURFACE FOR A RANGE (GRID) OF VALUES OF p AND q, AND SELECT THE VALUES CORRESPONDING TO THE MAXIMUM VALUE OF THE LIKELIHOOD SURFACE. THIS APPROACH IS NOT PRACTICAL FOR SITUATIONS INVOVLING A LARGE NUMBER OF PARAMETERS (SUCH AS MANY MULTIVARIATE APPLICATIONS).
TESTS OF MODEL ADEQUACY
THE PRIMARY GOAL IS TO OBTAIN A MODEL REPRESENTATION THAT REPRESENTS THE BASIC STOCHASTIC NATURE OF AN OBSERVED PROCESS WELL, IN AN EFFICIENT MANNER, I.E., WITH AS SMALL A NUMBER OF PARAMETERS AS IS REASONABLY POSSIBLE.
TESTS MAY BE APPLIED TO DETERMINE WHETHER φs AND θs AT SPECIFIED LAGS SHOULD BE RETAINED IN A PRELIMINARY MODEL. THE USUAL PROCEDURE IS TO TEST THE SIGNIFICANCE OF PARAMETERS FOR HIGHER LAGS FIRST.
A VERY IMPORTANT ASSUMPTION OF THE BOX-JENKINS MODELS IS THE ASSUMPTION THAT THE MODEL RESIDUALS (at’s) ARE UNCORRELATED, I.E., FORM A WHITE NOISE SEQUENCE. THE VALIDITY OF THIS ASSUMPTION MAY BE TESTED FROM THE AVAILABLE DATA. TESTS OF WHITENESS MAY INVOLVE EITHER THE AUTOCORRELATON FUNCTION OR THE SPECTRAL DENSITY FUNCTION. TESTS OF THIS ASSUMPTION INCLUDE THE GRENANDER-ROSENBLATT TEST, THE KOLMOGOROV-SMIRNOV TEST WITH THE LIILLIFORS CORRECTION, THE DURBIN-WATSON TEST, AND THE LJUNG-BOX TEST. FOR AN APPROPRIATE MODEL, THE MODEL RESIDUALS SHOULD APPEAR TO BE A WHITE NOISE PROCESS.
FOR LARGE n (THE SAMPLE
SIZE, AFTER DIFFERENCING TO ACHIEVE STATIONARITY) THE ESTIMATED
AUTOCORRELATIONS OF A WHITE NOISE SEQUENCE ARE APPROXIMATELY UNCORRELATED AND
NORMALLY DISTRIBUTED, WITH MEAN ZERO AND VARIANCE 1/n. IF, FOR A FITTED MODEL,
AN ESTIMATED AUTOCORRELATION EXCEEDS 1.96/![]() IN MAGNITUDE, THIS MAY BE VIEWED AS EVIDENCE THAT THE
MODEL RESIDUALS ARE NOT WHITE. UNFORTUNATELY, THE FACT THAT AN ESTIMATED
AUTOCORRELATION DOES NOT EXCEED THIS LEVEL MAY NOT BE VIEWED AS EVIDENCE
THAT THE AUTOCORRELATION IS ZERO. THE REASON FOR THIS IS THAT IF THE MODEL
RESIDUALS ARE NOT WHITE, THEN THE VARIANCE OF THE ESTIMATED AUTOCORRELATIONS
MAY BE VERY MUCH SMALLER THAN 1/n. FOR EXAMPLE, IN AN AUTOREGRESSIVE MODEL WITH
A SINGLE PARAMETER φ, THE VARIANCE OF THE LAG-ONE AUTOCORRELATION IS φ2/n. SO, IF φ IS AT ALL APPRECIABLE IN MAGNITUDE, THE VARIANCE OF
THE LAG-ONE AUTOCORRELATION IS SUBSTANTIALLY LESS THAN 1/n. IF THE VALUE 1.96/
IN MAGNITUDE, THIS MAY BE VIEWED AS EVIDENCE THAT THE
MODEL RESIDUALS ARE NOT WHITE. UNFORTUNATELY, THE FACT THAT AN ESTIMATED
AUTOCORRELATION DOES NOT EXCEED THIS LEVEL MAY NOT BE VIEWED AS EVIDENCE
THAT THE AUTOCORRELATION IS ZERO. THE REASON FOR THIS IS THAT IF THE MODEL
RESIDUALS ARE NOT WHITE, THEN THE VARIANCE OF THE ESTIMATED AUTOCORRELATIONS
MAY BE VERY MUCH SMALLER THAN 1/n. FOR EXAMPLE, IN AN AUTOREGRESSIVE MODEL WITH
A SINGLE PARAMETER φ, THE VARIANCE OF THE LAG-ONE AUTOCORRELATION IS φ2/n. SO, IF φ IS AT ALL APPRECIABLE IN MAGNITUDE, THE VARIANCE OF
THE LAG-ONE AUTOCORRELATION IS SUBSTANTIALLY LESS THAN 1/n. IF THE VALUE 1.96/![]() WERE USED TO DECIDE WHETHER THE LAG-ONE
AUTOCORRELATION WERE DIFFERENT FROM ZERO, THERE COULD (DEPENDING ON THE VALUE
OF φ)
BE A LARGE CHANGE OF WRONGLY DECIDING THAT THE TRUE LAG-ONE AUTOCORRELATION WAS
ZERO, WHEN IT WAS NOT.
WERE USED TO DECIDE WHETHER THE LAG-ONE
AUTOCORRELATION WERE DIFFERENT FROM ZERO, THERE COULD (DEPENDING ON THE VALUE
OF φ)
BE A LARGE CHANGE OF WRONGLY DECIDING THAT THE TRUE LAG-ONE AUTOCORRELATION WAS
ZERO, WHEN IT WAS NOT.
AN APPROXIMATE PORTMANTEAU TEST OF A FITTED ARIMA(p,d,q) MODEL WAS PROPOSED BY BOX AND PIERCE. IF THE FITTED MODEL IS APPROPRIATE, THEN THE STATISTIC
![]()
IS APPROXIMATELY
DISTRIBUTED AS χ2(K-p-q),
WHERE ![]() DENOTES THE k-th ESTIMATED AUTOCORRELATION AND n = N -d IS THE NUMBER OF OBSERVATIONS REMAINING AFTER
DIFFERENCING TO ACHIEVE STATIONARITY.
DENOTES THE k-th ESTIMATED AUTOCORRELATION AND n = N -d IS THE NUMBER OF OBSERVATIONS REMAINING AFTER
DIFFERENCING TO ACHIEVE STATIONARITY.
IN PRACTICE, IT WAS OBSERVED THAT FOR SAMPLES OF THE SIZE OFTEN ENCOUNTERED IN PRACTICE, THE VALUE OF THE Q STATISTIC TENDS TO BE SMALLER THAN χ2(K-p-q). LJUNG AND BOX PROPOSED A MODIFIED FORM OF THE TEST STATISTIC,
![]()
THIS STATISTIC HAS THE MEAN K – p -q OF THE χ2(K-p-q) DISTRIBUTION. IT IS A MORE SATISFACTORY STATISTIC BECAUSE THE VARIANCE OF rk(a) FOR A WHITE NOISE SERIES IS CLOSER TO (n – k))/(n(n + 2)) THE VALUE 1/n ASSUMED FOR THE BOX-PIERCE TEST.
THE STANDARD TEST FOR
WHITENESS, THEN, IS THE LJUNG-BOX TEST, WHICH TESTS WHETHER THE FIRST K
AUTOCORRELATIONS OF THE ERRORS FOR A FITTED MODEL ARE ZERO. SUPPOSE THAT THE
FITTED MODEL IS ARIMA(p,d,q). THE VALUE OF K IS CHOSEN SO THAT THE WEIGHTS ![]() OF THE MODEL,
WRITTEN IN THE FORM
OF THE MODEL,
WRITTEN IN THE FORM ![]() ARE SMALL AFTER LAG j = K. LET N DENOTE THE TOTAL NUMBER OF OBSERVATIONS AND n =
N – d DENOTE THE NUMBER OF OBSERVATIONS AFTER DIFFERENCING d TIMES TO ACHIEVE
STATIONARITY. DENOTE THE ESTIMATED MODEL RESIDUALS AS
ARE SMALL AFTER LAG j = K. LET N DENOTE THE TOTAL NUMBER OF OBSERVATIONS AND n =
N – d DENOTE THE NUMBER OF OBSERVATIONS AFTER DIFFERENCING d TIMES TO ACHIEVE
STATIONARITY. DENOTE THE ESTIMATED MODEL RESIDUALS AS ![]() AND DENOTE THE ESTIMATED AUTOCORRELATION OF THE
SEQUENCE OF ESTIMATED MODEL RESIDUALS AS
AND DENOTE THE ESTIMATED AUTOCORRELATION OF THE
SEQUENCE OF ESTIMATED MODEL RESIDUALS AS ![]() THE TEST STATISTISTIC IS
THE TEST STATISTISTIC IS
![]()
THIS TEST STATISTIC IS APPROXIMATELY DISTRIBUTED AS A χ2(K-p-q) VARIATE.
IF THE AVAILABLE DATA ARE LIMITED, TESTS OF MODEL ADEQUACY ARE PERFORMED USING ALL OF THE AVAILABLE DATA. IF SUFFICIENT DATA ARE AVAILABLE, A PREFERRED PROCEDURE IS TO ESTIMATE THE MODEL FROM ONE DATA SET AND ASSESS MODEL PERFORMANCE FROM A SEPARATE DATA SET.
MEASURES OF MODEL EFFICIENCY (INFORMATION CRITERIA): AIC, BIC, HQC
IN SPECIFYING A MODEL, A BETTER FIT (LOWER VARIANCE OF THE RESIDUALS) MAY BE ACHIEVED WITH MORE PARAMETERS, BUT THE MODEL MAY IN FACT EXHIBIT LOWER PERFORMANCE FOR PREDICTION (FORECASTING) OR CONTROL THAN A MODEL HAVING FEWER PARAMETERS. THAT IS, THERE IS A TRADE-OFF BETWEEN MODEL PRECISION (GOODNESS OF FIT) AND MODEL COMPLEXITY.
THREE STANDARD PROCEDURES ARE AVAILABLE FOR ASSISTING THE CHOICE OF A MODEL (FROM A SELECTION OF ALTERNATIVE MODELS THAT PASS TESTS OF MODEL ADEQUACY). THESE PROCEDURES FORM A MEASURE THAT INCLUDES A TERM REPRESENTING THE MAXIMIZED LIKELIHOOD AND A TERM REPRESENTING MODEL COMPLEXITY.
AKAIKE INFORMATION CRITERION (AIC)
![]()
WHERE r DENOTES THE NUMBER OF MODEL PARAMETERS (E.G., r = p + q FOR A NONSEASONAL ARMA MODEL WITHOUT A MEAN, OR r = p + q + 1 FOR A NONSEASONAL MODEL WITH A MEAN).
BAYESIAN (SCHWARZ) INFORMATION CRITERION (BIC)
![]()
HANNAN-QUINN CRITERION (HQC)
![]()
IF THE TRUE PROCESS IS AN ARMA(p,q) PROCESS, IT CAN BE SHOWN THAT THE BIC AND HQC ARE CONSISTENT IN THE SENSE THAT AS THE SAMPLE SIZE BECOMES VERY LARGE, THEY SELECT THE CORRECT MODEL (VALUES OF p AND q). THE AIC MAY SELECT A MODEL THAT IS SLIGHTLY MORE COMPLEX. IF THE TRUE PROCESS IS NOT A FINITE-ORDER ARMA PROCESS, THEN THE AIC HAS THE PROPERTY THAT AS THE SAMPLE SIZE BECOMES LARGE IT WILL SELECT, FROM A SET OF ARMA MODELS, THE ONE THAT IS CLOSEST TO THE TRUE PROCESS (WHERE CLOSENESS IS MEASURED BY THE KULLBACK-LEIBLER DIVERGENCE, A MEASURE OF DISPARITY BETWEEN MODELS).
IN THE PRECEDING FORMULAS FOR THE INFORMATION CRITERIA, THE FIRST TERM,
![]()
MAY BE APPROXIMATED BY
![]()
THE NATURAL LOGARITHM OF THE ESTIMATED VARIANCE OF THE RESIDUALS OF THE FITTED MODEL.
A DRAWBACK OF THE
INFORMATION CRITERIA IS THAT THEIR USE REQUIRES THE FITTING OF A POTENTIALLY LARGE
NUMBER OF ALTERNATIVE ARMA(p,q) MODELS, FOR ALTERNATIVE VALUES OF p AND q.
HANNAN AND RISSANEN DEVELOPED A METHOD FOR AVOIDING THIS PROBLEM. THEIR
APPROACH IS AS FOLLOWS. FIRST, ESTIMATE AN AR MODEL OF HIGH ORDER, AND USE THE
RESIDUALS OF THIS MODEL AS APPROXIMATIONS FOR THE RESIDUALS OF THE CORRECT
MODEL. THEN, REGRESS THE OBSERVED VALUE zt ON p PREVIOUS
OBSERVATIONS AND q APPROXIMATE RESIDUALS, FOR VARIOUS VALUES OF p AND q. DENOTE
THE ESTIMATED ERROR VARIANCE OF EACH OF THESE MODELS BY ![]() THEN, USING THE BIC, SELECT THE VALUES OF p AND q THAT
MINIMIZE
THEN, USING THE BIC, SELECT THE VALUES OF p AND q THAT
MINIMIZE
![]()
I.E., THE BIC. (FITTING THESE MODELS IS EASIER THAN FITTING ARMA(p,q) MODELS BECAUSE THEY ARE LINEAR STATISTICAL MODELS (REGRESSION MODELS), NOT NONLINEAR MODELS (AS ARE ARMA MODELS).) HANNAN AND RISSANEN SHOW THAT THE ESTIMATORS OF p AND q DETERMINED BY THIS METHOD CONVERGE ALMOST SURELY TO THE CORRECT VALUES.
GENERAL FORM OF AN ARIMA MODEL
THE GENERAL FORM OF A (NONSEASONAL) ARIMA MODEL IS
![]()
WHERE θ0 IS A CONSTANT,
![]()
![]()
AND
![]()
IN MODELS CONTAINING DIFFERENCE OPERATORS (FACTORS OF (1 – B)), θ0 IS USUALLY ZERO. THE MODEL ERROR TERMS, THE a’s, ARE REFERRED TO AS “SHOCKS.”
THE OPERATOR φ(B) IS CALLED THE AUTOREGRESSIVE OPERATOR. IT IS ASSUMED TO BE STATIONARY, I.E., TO HAVE ROOTS (SOLUTIONS TO φ(B) = 0) OUTSIDE THE UNIT CIRCLE.
THE OPERATOR ϕ(B) IS CALLED THE GENERALIZED AUTOREGRESSIVE OPERATOR. IT CONTAINS d ROOTS ON THE UNIT CIRCLE (SPECIFICALLY, ALL EQUAL TO ONE).
THE OPERATOR θ(B) IS CALLED THE MOVING AVERAGE OPERATOR. IT IS ASSUMED TO BE INVERTIBLE, I.E., TO HAVE ROOTS OUTSIDE THE UNIT CIRCLE.
IN THE FOLLOWING WE SHALL ASSUME THAT θ0 = 0.
ALTERNATIVE FORMS OF AN ARIMA MODEL
THREE DIFFERENT FORMS OF AN ARIMA MODEL ARE
1. THE DIFFERENCE EQUATION FORM, IN WHICH THE CURRENT VALUE OF THE OUTPUT, zt, IS EXPRESSED IN TERMS OF THE z’s AND CURRENT AND PREVIOUS VALUES OF THE a’s.
2. THE RANDOM-SHOCK FORM OF THE MODEL, IN WHICH THE CURRENT VALUE OF zt IS EXPRESSED IN TERMS OF CURRENT AND PREVIOUS a’s.
3. THE INVERTED FORM OF THE MODEL, IN WHICH THE CURRENT VALUE OF zt IS EXPRESSED IN TERMS OF A WEIGHTED SUM OF PREVIOUS z’s AND THE CURRENT a (I.E., at).
DEPENDING ON WHAT IS BEING DISCUSSED, ONE FORM IS MORE USEFUL THAN THE OTHERS.
THESE THREE FORMS OF AN ARIMA MODEL ARE NOW DESCRIBED IN FURTHER DETAIL.
DIFFERENCE-EQUATION FORM OF THE MODEL
THE GENERAL FORM OF THE MODEL IS
![]()
FOR THE DIFFERENCE-EQUATION FORM WE SIMPLY EXPAND THE ϕ AND θ POLYNOMIALS AND TRANSFER ALL BUT THE CURRENT zt TO THE RIGHT-HAND-SIDE OF THE MODEL EQUATION. THAT IS:
![]()
OR
![]()
OR
![]()
THE GENERAL FORM OF THE MODEL IS USED TO COMPACTLY DESCRIBE THE MODEL, AND TO SUCCINCTLY COMPARE ONE MODEL TO ANOTHER.
RANDOM-SHOCK FORM OF THE MODEL
IT WAS DISCUSSED EARLIER THAT A STATIONARY STOCHASTIC PROCESS MAY BE EXPRESSED AS AN INFINITE SERIES (THE WOLD DECOMPOSITION):
![]()
WHERE
![]()
SINCE A GENERAL ARIMA MODEL IS NOT STATIONARY, HOWEVER, THE WOLD THEOREM DOES NOT APPLY, AND IT CANNOT BE ASSERTED ON THAT BASIS THAT AN INFINITE-SERIES REPRESENTATION EXISTS. IN FACT, FOR NONSTATIONARY PROCESSES, THIS IS NOT POSSIBLE. IT IS POSSIBLE, HOWEVER, TO EXPRESS AN ARIMA MODEL IN A TRUNCATED (FINITE-SERIES) FORM, WHICH IS USEFUL FOR UPDATING FORECASTS AND CALCULATING FORECAST VARIANCES.
THIS REPRESENTATION IS AS FOLLOWS:
![]()
WHERE Ck(t-k) IS THE COMPLEMENTARY FUNCTION, OR GENERAL SOLUTION OF THE DIFFERENCE EQUATION
![]()
IT CAN BE SHOWN THAT THIS REPRESENTATION IS EQUAL TO:
![]()
WHERE Ek[zt] DENOTES THE CONDITIONAL EXPECTATION OF zt AT TIME k. SEE BJRL pp. 97-105 FOR DISCUSSION.
THE Ψ WEIGHTS ARE OBTAINED BY EQUATING COEFFICIENTS OF B IN THE EXPRESSION
![]()
THAT IS, RECURSIVELY FROM THE EXPRESSION
![]()
WHERE Ψ0 = 1, Ψj = 0 FOR j < 0 and θj = 0 FOR j > q.
IT CAN BE SHOWN THAT
![]()
THIS EXPRESSION SHOWS HOW TO UPDATE A FORECAST FROM ONE POINT IN TIME (I.E., t) TO THE NEXT.
INVERTED FORM OF THE MODEL
IN THE GENERAL FORM OF THE MODEL,
![]()
THE POLYNOMIAL θ(B) HAS ROOTS OUTSIDE THE UNIT CIRCLE, I.E., THE PROCESS IS INVERTIBLE, AND MAY BE EXPRESSED AS
![]()
THE π WEIGHTS ARE DETERMINED IN THE SAME WAY AS THE Ψ WEIGHTS WERE, ABOVE.
WE WRITE
![]()
AND OBTAIN THE π WEIGHTS BY EQUATING COEFFICIENTS OF B IN THE EXPRESSION
![]()
THIS YIELDS
![]()
HENCE THE π WEIGHTS MAY BE DETERMINED RECURSIVELY FROM
![]()
WHERE π0 = -1, πj = 0 FOR j < 0 and ϕj = 0 FOR j > p+d.
THE INVERTED FORM OF THE MODEL CAN BE WRITTEN AS
![]()
SINCE THE SERIES Σπj IS CONVERGENT, THE WEIGHTS πj DIE OUT, SO THAT THE CURRENT VALUE OF THE TIME SERIES DEPENDS MAINLY ON VALUES OF πj IN THE RECENT PAST. THIS IS IN CONTRAST TO THE RANDOM-SHOCK MODEL,
![]()
WHERE THE WEIGHTS DO NOT
DIE OUT FOR NONSTATIONARY MODELS (I.E., THE TERM ![]() DOES NOT DECREASE TO ZERO AS k INCREASES).
DOES NOT DECREASE TO ZERO AS k INCREASES).
FORECASTING
ONCE A MODEL PASSES THE VARIOUS TESTS OF MODEL ADEQUACY, IT MAY BE USED AS A BASIS FOR FORECASTING, I.E., PREDICTING THE FUTURE VALUE OF THE PROCESS, GIVEN AN OBSERVED SEQUENCE OF OBSERVATIONS.
THE OBJECTIVE IS TO ESTIMATE THE VALUE OF
![]()
FOR INTEGER ![]() WHERE WE HAVE
OBSERVATIONS
WHERE WE HAVE
OBSERVATIONS
![]()
THE TIME t IS CALLED THE ORIGIN
OF THE FORECAST, AND THE VALUE OF ![]() ISCALLED THE LEAD TIME OF THE FORECAST. THIS
FORECAST WILL BE DENOTED BY
ISCALLED THE LEAD TIME OF THE FORECAST. THIS
FORECAST WILL BE DENOTED BY
![]()
THE STANDARD APPROACH TO FORECASTING IS TO DETERMINE THE FORECAST THAT HAS MINIMUM MEAN SQUARED ERROR OF PREDICTION, I.E. THE ONE FOR WHICH
![]()
IS MINIMIZED. IT CAN BE
SHOWN THAT THIS FORECAST IS THE EXPECTED VALUE OF ![]() CONDITIONAL ON THE OBSERVATIONS
CONDITIONAL ON THE OBSERVATIONS ![]() :
:
![]()
TO CALCULATE THE FORECAST, THIS EXPECTED VALUE MUST BE DETERMINED. WHILE THIS PRESENTATION DOES NOT GENERALLY PRESENT MATHEMATICAL PROOFS, THE DERIVATION OF AN EXPRESSION FOR THIS EXPECTED VALUE IS STRAIGHTFORWARD IN THE CASE IN WHICH THE MODEL IS STATIONARY, AND WILL BE PRESENTED.
IN THE STATIONARY CASE, WE MAY WRITE
![]()
THE OBJECTIVE IS TO
CONSTRUCT A FORECAST ![]() OF
OF ![]() WHICH IS A LINEAR COMBINATION OF CURRENT AND PREVIOUS
OBSERVATIONS, zt, zt-1, zt-2,…, OR,
EQUIVALENTLY, OF CURRENT AND PREVIOUS SHOCKS, at, at-1, at-2….
WHICH IS A LINEAR COMBINATION OF CURRENT AND PREVIOUS
OBSERVATIONS, zt, zt-1, zt-2,…, OR,
EQUIVALENTLY, OF CURRENT AND PREVIOUS SHOCKS, at, at-1, at-2….
LET US DENOTE THE FORECAST AS
![]()
WHERE THE WEIGHTS Ψj* ARE TO BE DETERMINED TO MINIMIZE THE MEAN- SQUARED ERROR OF PREDICTION (OR MEAN SQUARED FORECAST ERROR). THE MEAN-SQUARED FORECAST ERROR IS
![]()
WHICH IS MINIMIZED BY
SETTING ![]() .
.
IT THEN FOLLOWS THAT
![]()
WHERE
![]()
IS THE ERROR OF THE
FORECAST ![]() AT LEAD TIME
AT LEAD TIME ![]() .
.
THE EXPECTED VALUE OF ![]() IS ZERO (SINCE THE EXPECTED VALUE OF EACH OF THE a’s
IS ZERO). THE VARIANCE OF
IS ZERO (SINCE THE EXPECTED VALUE OF EACH OF THE a’s
IS ZERO). THE VARIANCE OF ![]() IS
IS
![]()
ASSUMING THAT THE at ARE INDEPENDENT, WE HAVE (IN THE STATIONARY CASE)
![]()
SO
![]()
THAT IS, THE MINIMUM (LINEAR)
MEAN-SQUARED-ERROR FORECAST AT ORIGIN t FOR LEAD TIME ![]() IS THE CONDITIONAL EXPECTATION OF
IS THE CONDITIONAL EXPECTATION OF ![]() AT TIME t. CONSIDERED AS A FUNCTION OF
AT TIME t. CONSIDERED AS A FUNCTION OF ![]() FOR FIXED T,
FOR FIXED T, ![]() IS CALLED THE FORECAST FUNCTION FOR ORIGIN t.
IS CALLED THE FORECAST FUNCTION FOR ORIGIN t.
NOTE THAT THE PRECEDING PROOF ASSUMED STATIONARITY. THE GENERAL FORM OF THE ARIMA MODEL IS NONSTATIONARY, AND DERIVATION OF THE FORECAST FUNCTION IN THE GENERAL (NONSTATIONARY) CASE IS A LITTLE DIFFERENT.
CALCULATION OF THE FORECAST MAY BE DONE IN THREE DIFFERENT WAYS, CORRESPONDING TO THE THREE DIFFERENT REPRESENTATIONS OF THE MODEL. IN THIS PRESENTATION, WE SHALL DISCUSS FORECASTING USING THE DIFFERENCE-EQUATION REPRESENTATION. SEE CHAPTER 5 (pp. 129 – 176) OF BJRL FOR DETAILED DISCUSSION.
FORECASTING USING THE DIFFERENCE-EQUATION FORM
THE FORMULA FOR CALCULATING FORECASTS FROM THE DIFFERENCE-EQUATION FORM OF AN ARIMA MODEL IS
![]()
WHERE ![]() DENOTES THE OBSERVED VALUE zt-j FOR j
>= 0 AND THE MOVING AVERAGE TERMS ARE NOT PRESENT FOR
DENOTES THE OBSERVED VALUE zt-j FOR j
>= 0 AND THE MOVING AVERAGE TERMS ARE NOT PRESENT FOR ![]() > q. THE VALUE OF THE MOVING AVERAGE TERM (MODEL
ERROR TERM) at IS ESTIMATED AS
> q. THE VALUE OF THE MOVING AVERAGE TERM (MODEL
ERROR TERM) at IS ESTIMATED AS
![]()
FORECASTING USING A DIFFERENCE EQUATION – ADDITIONAL DETAILS
THIS SUBSECTION PRESENTS SOME ADDITIONAL DISCUSSION OF THE PROCEDURE FOR CALCULATING A FORECAST FROM THE DIFFERENCE-EQUATION REPRESENTATION. THE ISSUE THAT IS ADDRESSED IS TO USE THE PRECEDING FORMULA, VALUES OF THE a’s MUST BE AVAILABLE FOR q TIMES PREVIOUS TO THE FORECAST ORIGIN. THE EASIEST WAY TO ESTIMATE THESE a’s IS TO COMPUTE FORECASTS FROM THE BEGINNING OF THE AVAILABLE SERIES, EVEN THOUGH FORECASTS ARE USUALLY DESIRED ONLY FROM THE LAST AVAILABLE OBSERVATION. THIS IS DONE AS FOLLOWS.
THE GENERAL ARIMA MODEL MAY BE EXPRESSED IN THE FORM
![]()
OR
![]()
OR
![]()
THIS FORM PROVIDES THE BASIS FOR AN ITERATIVE METHOD FOR CALCULATING THE FORECAST. RECALL THAT IN AN ACCEPTABLE ARIMA MODEL, THE θ POLYNOMIAL IS INVERTIBLE, I.E., ITS ROOTS ARE OUTSIDE THE UNIT CIRCLE. THIS IMPLIES THAT THE INFLUENCE OF THE MODEL ERROR TERMS (OR “SHOCKS”) ON FUTURE VALUES OF THE PROCESS DIMINISHES IN TIME.
TO IMPLEMENT THIS METHOD, FORECASTING IS DONE FROM TIME ORIGIN p + d:
![]()
FOR THIS FIRST FORECAST, THE ERROR TERMS ap+1, ap,…,ap-q+1 ARE ESTIMATED BY THEIR EXPECTED VALUES, ZEROS. THIS YIELDS
![]()
THE VALUE OF ap+1
IS ESTIMATED AS THE DIFFERENCE BETWEEN THE FORECAST VALUE ![]() AND THE TRUE (OBSERVED) VALUE zp+d+1:
AND THE TRUE (OBSERVED) VALUE zp+d+1:
![]()
THE SAME PROCEDURE IS
APPLIED TO CONSTRUCT ![]() , BUT NOW USING THE ESTIMATED VALUE
, BUT NOW USING THE ESTIMATED VALUE ![]() FOR ap+1. THE ERROR TERM ap+2
IS ESTIMATED AS
FOR ap+1. THE ERROR TERM ap+2
IS ESTIMATED AS
![]()
AFTER MAKING q FORECASTS IN THIS WAY, ESTIMATED VALUES ARE AVAILABLE FOR ALL ats REQUIRED BY THE MODEL EQUATION.
THIS FORECAST PROCESS IS CONTINUED UP TO THE PRESENT TIME, t. FOR MAKING FORECASTS OF zt BEYOND TIME t, THE VALUES OF at (at+1, at+2,…) ARE UNKNOWN, AND THEIR EXPECTED VALUES, ZEROS, ARE USED.
SINCE THE PROCESS IS ASSUMED INVERTIBLE, THE EFFECT OF ASSUMING ZEROS FOR THE INITIAL VALUES OF THE ats DIES OUT AS THE ITERATIVE FORECASTING PROCEDURE CONTINUES.
UPDATING FORECASTS USING Ψ WEIGHTS
ONCE AN INITIAL FORECAST HAS BEEN DETERMINED, THERE IS AN EASY WAY TO CALCULATE FUTURE FORECASTS FROM IT, AS NEW OBSERVATIONS BECOME AVAILABLE. THIS FORMULA IS:
![]()
WHERE
![]()
FORECAST ERROR VARIANCE AND PROBABILITY LIMITS
THE FORECAST ERROR VARIANCES ARE DETERMINED FROM FORMULAS THAT INVOLVE THE Ψ WEIGHTS. THE RECURSIVE FORMULA FOR DETERMINING THOSE WEIGHTS WAS PRESENTED ABOVE (IN THE SECTION DEALING WITH THE THREE ALTERNATIVE FORMS OF AN ARIMA MODEL).
THE VARIANCE OF THE FORECAST ERROR WAS GIVEN ABOVE, IN TERMS OF THE Ψ WEIGHTS, AS
![]()
IF THE MODEL ERROR TERMS ARE APPROXIMATELY NORMALLY DISTRIBUTED, 95% PROBABILITY LIMITS ARE EQUAL TO THE FORECAST ESTIMATE PLUS AND MINUS 1.96 TIMES THE SQUARE ROOT OF THE VARIANCE.
THE PRECEDING IS A METHOD OF MAKING FORECASTS ASSUMING THAT THE TRUE MODEL IS KNOWN. IN PRACTICE, THE MODEL IS NOT KNOWN, AND ESTIMATED VALUES ARE USED FOR THE MODEL PARAMETERS. IT CAN BE SHOWN THAT FORECASTS BASED ON ESTIMATED PARAMETER VALUES ARE UNBIASED.
THE FORMULA PRESENTED ABOVE FOR THE FORECAST ERROR VARIANCE ASSUMED THAT THE PARAMETER VALUES WERE KNOWN, NOT ESTIMATED. FOR MODELS ESTIMATED FROM LARGE SAMPLES, THESE FORMULAS MAY BE USED. FOR MODELS ESTIMATED FROM SMALL SAMPLES, MODIFIED FORMULAS THAT TAKE INTO ACCOUNT THE ERROR ASSOCIATED WITH PREDICTION OF THE MODEL PARAMETERS ARE AVAILABLE AND SHOULD BE USED (E.G., BOOTSTRAPPING).
IMPULSE RESPONSE FUNCTION
ABOVE, EXPRESSIONS WERE PRESENTED FOR THE IMPULSE RESPONSE FUNCTION FOR A SPECIFIED (TRUE) MODEL, IN THE CASE OF A STATIONARY STOCHASTIC PROCESS. WHEN THE TRUE MODEL IS NOT KNOWN AND THE MODEL PARAMETERS MUST BE ESTIMATED FROM DATA, THE IMPULSE RESPONSE FUNCTION IS ESTIMATED BY SUBSTITUTING ESTIMATED PARAMETER VALUES IN THE FORMULAS FOR THE TRUE MODEL. THIS PROCEDURE PRODUCES CONSISTENT ESTIMATES OF THE IMPULSE RESPONSE FUNCTION.
FOR A HOMOGENEOUS NONSTATIONARY PROCESS, AS MENTIONED, IT IS NOT POSSIBLE TO EXPRESS THE IMPULSE RESPONSE FUNCTION AS AN INFINITE SERIES. IN THIS CASE, A FINITE NUMBER OF THE Ψ WEIGHTS MAY BE CALCULATED, AS DESCRIBED IN THE SECTION THAT DESCRIBED REPRESENTING AN ARIMIA PROCESS IN TERMS OF RANDOM SHOCKS.
AS MENTIONED EARLIER, THE IMPULSE RESPONSE FUNCTION INDICATES THE AVERAGE CHANGE IN THE OUTPUT (zt) CORRESPONDING TO A UNIT CHANGE IN THE INPUT (at), FOR at GENERATED ACCORDING TO A CAUSAL MODEL. IF THE MODEL IS ESTIMATED FROM DATA IN WHICH THE at ARE SIMPLY OBSERVED, NOT CONTROLLED (FORCED), THEN THE IRF IS AN ESTIMATE OF THE CHANGE TO BE EXPECTED IN THE OUTPUT CORRESPONDING TO AN OBSERVED UNIT CHANGE IN THE INPUT. IF THE MODEL IS ESTIMATED FROM EXPERIMENTAL-DESIGN DATA IN WHICH RANDOMIZED FORCED CHANGES ARE MADE IN THE INPUT, THEN THE IRF IS AN ESTIMATE OF THE CHANGE TO BE EXPECTED IN THE OUTPUT IF FORCED CHANGES ARE MADE AS UNDER THE EXPERIMENTAL CONDITONS FOR WHICH THE DATA USED TO ESTIMATE THE MODEL WERE COLLECTED.
THE IMPULSE RESPONSE FUNCTION IS OF GREATER INTEREST FOR MODELS THAT CONTAIN COVARIATES (VARIABLES OF THE MODEL OTHER THAN MODEL ERROR TERMS) THAN FOR MODELS THAT DO NOT. THAT IS, IT IS OF GREATER INTEREST TO KNOW THE RESPONSE OF A CHANGE IN AN EXPLANATORY VARIABLE THAN IN A MODEL ERROR (“SHOCK”).
ALTERNATIVE REPRESENTATIONS: UNIQUENESS OF MODEL, JOINT PDF, ACF (NORMAL)
UNDER THE ASSUMPTION OF INVERTIBILITY, IF A PARTICULAR AUTOCORRELATION FUNCTION CORRESPONDS TO AN ARMA MODEL, THEN THAT MODEL IS UNIQUE (AMONG ALL ARMA MODELS).
MORE SPECIFICALLY, A STATIONARY INVERTIBLE ARIMA STOCHASTIC PROCESS IS UNIQUELY DEFINED BY THE JOINT PROBABILITY DISTRIBUTION FUNCTION OF A SEQUENCE OF OBSERVED VALUES (zt, zt+1, …, zt+k) OR BY THE ARIMA MODEL SPECIFICATION. IF THE PROCESS OBEYS A NORMAL DISTRIBUTION, THEN IT IS CHARACTERIZED (UNIQUELY DEFINED) BY THE MEAN, VARIANCE, AND AUTOCOVARIANCE FUNCTION.
ALTERNATIVE REPRESENTATIONS: STATE SPACE, KALMAN FILTER
THE PRECEDING MATERIAL DESCRIBES THE BASIC THEORY OF UNIVARIATE TIME SERIES ANALYSIS, USING ARIMA STOCHASTIC PROCESS MODELS. AN ARIMA MODEL IS USED TO REPRESENT THE THEORETICAL (TRUE, POPULATION) STOCHASTIC PROCESS THAT GENERATES THE DATA, AND FORECASTS ARE CONSTRUCTED DIRECTLY FROM THE ESTIMATED ARIMA MODEL.
AN ALTERNATIVE METHODOLOGY FOR CONSTRUCTING TIME SERIES MODELS AND GENERATING FORECASTS IS BASED ON THE USE OF STATE SPACE REPRESENTATIONS OF TIME SERIES. THE STATE SPACE METHODOLOGY IS MORE GENERAL THAN THE METHODOLOGY PRESENTED ABOVE, IN THAT IT ALLOWS FOR MEASUREMENT ERRORS (THE PRECEDING DISCUSSION ASSUMES THAT THE PROCESS VALUE, zt, IS KNOWN EXACTLY, WITHOUT MEASUREMENT ERROR), AND ALLOWS FOR TIME-VARYING PARAMETERS (IN THE PRECEDING DISCUSSION, THE MODEL PARAMETERS ARE FIXED).
THE OPTIMAL FORECASTER FOR A STATE SPACE REPRESENTATION IS CALLED THE KALMAN FILTER.
THE STATE SPACE METHODOLOGY MAY BE APPLIED EITHER TO UNIVARIATE OR MULTIVARIATE TIME SERIES. THE FORMULAS INVOLVED ARE IDENTICAL IN THE UNIVARIATE AND MULTIVARIATE CASES. TO AVOID REDUNDANCY, DISCUSSION OF STATE SPACE FORECASTING AND THE KALMAN FILER IS DEFERRED UNTIL THE DISCUSSION OF MULTIVARIATE TIME SERIES MODELS.
EXTENSIONS: ARCH, GARCH
IN THE PRECEDING DISCUSSION, THE (STATIONARITY) ASSUMPTION WAS MADE THAT THE ERROR VARIANCE OF THE STOCHASTIC PROCESS IS CONSTANT (OVER TIME). IN SOME IMPORTANT APPLICATIONS, THIS ASSUMPTION IS UNTENABLE. FOR EXAMPLE, THE VARIABILITY OF STOCK AND COMMODITY PRICES IS KNOWN TO FLUCTUATE OVER TIME.
A STOCHASTIC PROCESS FOR WHICH THE ERROR VARIANCE IS CONSTANT IS CALLED A HOMOSCEDASTIC (OR HOMOSKEDASTIC) PROCESS. A STOCHASTIC PROCESS FOR WHICH THE ERROR VARIANCE IS NOT CONSTANT IS CALLED A HETEROSCEDASTIC (OR HETEROSKEDASTIC) PROCESS.
HETEROSCEDASTICITY IS A FORM OF NONSTATIONARY BEHAVIOR (AS IS THE HOMOGENEOUS NONSTATONARY BEHAVIOR ASSOCIATED WITH ROOTS OF THE AR POLYNOMIAL BEING LOCATED ON THE UNIT CIRCLE).
STANDARD MODELS HAVE BEEN DEVELOPED TO REPRESENT HETEROSCEDASTIC BEHAVIOR. THESE MODELS ARE CALLED AUTOREGRESSIVE CONDITIONAL HETEROSCEDASTICITY (ARCH) MODELS. IN SUCH MODELS, THE VARIANCE OF THE CURRENT ERROR TERM IS A FUNCTION OF THE SIZES OF THE ERROR TERMS FOR PREVIOUS TIME PERIODS.
FOR AN ARCH MODEL, THE ERROR VARIANCE OBEYS AN AUTOREGRESSIVE (AR) MODEL. IF THE ERROR VARIANCE OBEYS AN AUTOREGRESSIVE MOVING AVERAGE MODEL (ARMA), THE MODELS IS CALLED A GENERALIZED AUTOREGRESSIVE CONDITIONAL HETEROSCEDASTICITY (GARCH) MODEL.
THE ARCH AND GARCH MODELS WILL NOT BE DESCRIBED HERE. DETAILED DESCRIPTIONS OF THESE MODELS ARE PRESENTED IN THE REFERENCES. THE BASIC APPROACH TO DEVELOPMENT OF ARCH AND GARCH MODELS IS THE SAME AS FOR THE HOMOSCEDASTIC MODELS DESCRIBED ABOVE. ALL THAT CHANGES IS THAT THE MODELS CONTAIN SOME ADDITIONAL PARAMETERS THAT DESCRIBE HOW THE VARIANCE CHANGES (E.G., USING AN ARMA MODEL TO REPRESENT THE VARIANCE).
DETAILED EXAMPLE OF THE DEVELOPMENT OF A SINGLE-VARIABLE UNIVARIATE TIME SERIES MODEL
IN THEIR ORIGINAL WORK, BOX AND JENKINS PRESENTED AN EXAMPLE IN WHICH AN ARIMA MODEL WAS DEVELOPED FOR A TIME SERIES OF MONTHLY AIRLINE TICKET SALES. THIS EXAMPLE HAS BEEN PRESENTED IN MANY TEXTS, INCLUDING BJRL (pp. 310-325), CRYER (pp. 240 – 244) AND STATA.
THIS EXAMPLE WILL NOW BE DESCRIBED IN DETAIL. NUMERICAL COMPUTATIONS ASSOCIATED WITH THIS ANALYSIS WILL SHOWN USING THE FREE BOX-JENKINS PROGRAM POSTED AT INTERNET WEBSITE http://www.foundationwebsite.org . THAT PROGRAM ESTIMATES SINGLE-VARIABLE BOX-JENKINS MODELS (SEASONAL OR NONSEASONAL) CONTAINING UP TO TWO PHI PARAMETERS AND TWO THETA PARAMETERS. IT PRODUCES FORECASTS, BUT NOT FORECAST ERROR VARIANCES. IT USES THE “CONDITIONAL” ESTIMATION PROCEDURE, IN WHICH THE VALUES OF MODEL RESIDUALS PRIOR TO THE OBSERVED TIME SERIES ARE REPLACED BY ZEROS. THESE ESTIMATES ARE SLIGHTLY DIFFERENT FROM THOSE PRODUCED USING UNCONDITIONAL ESTIMATION (AS IN STATA).
THE DATA ARE LOGARITHMS OF INTERNATIONAL AIRLINE TICKET SALES FROM JANUARY 1949 THROUGH DECEMBER 1960, A TOTAL OF n = 144 OBSERVATIONS.
PROGRAM OUTPUT IS SHOWN, ON THE PAGES THAT FOLLOW, FOR THE FOLLOWING CASES:
1. RAW DATA (ALREADY TRANSFORMED TO LOGARITHMS)
2. DIFFERENCING OF SPAN 1
3. DIFFERENCING OF SPAN 12
4. DIFFERENCING OF SPANS 1 AND 12
5. DIFFERENCING OF SPANS 1 AND 12, AND ESTIMATION OF θ1 AND θ12.
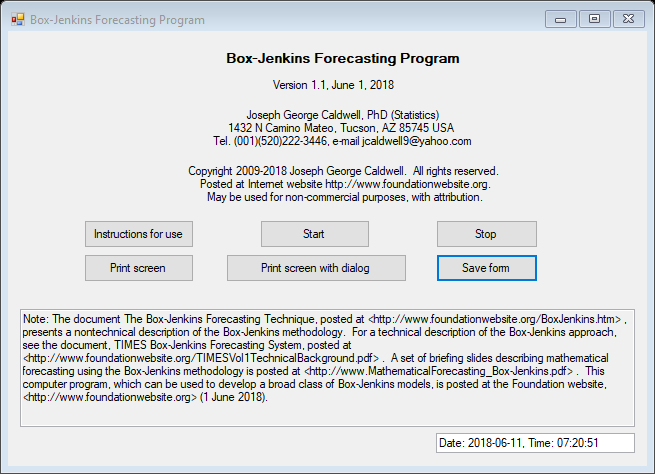
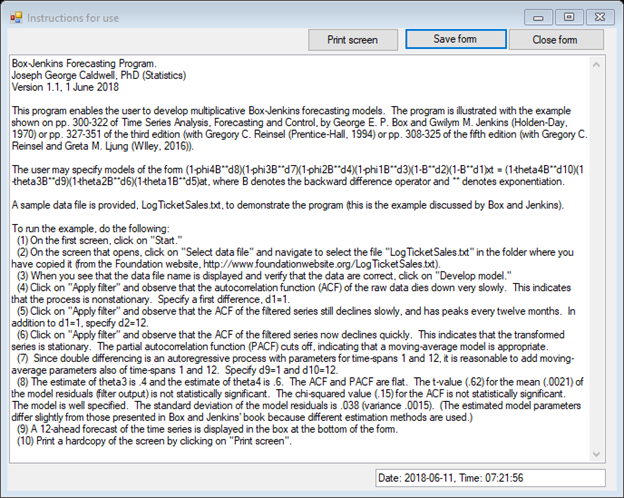


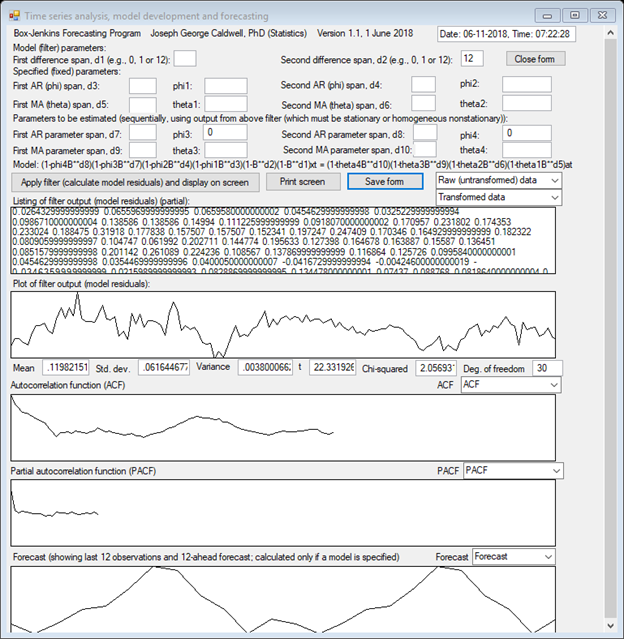
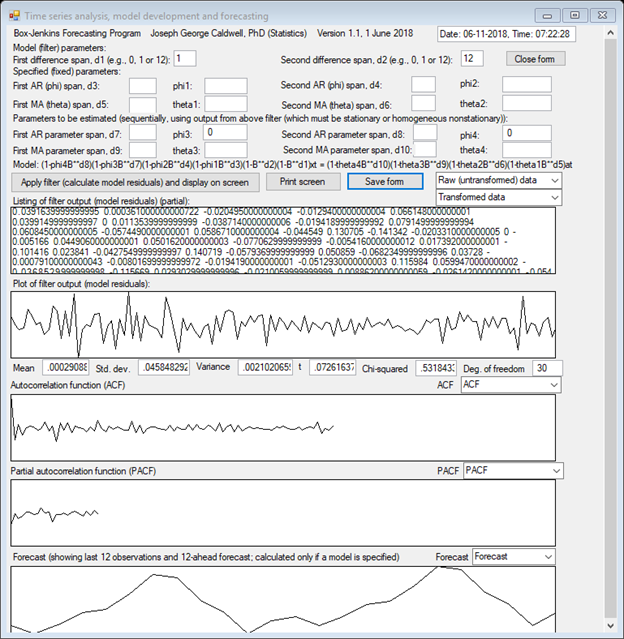
THE PLOT OF THE TIME SERIES CLEARLY SHOWS A NONSTATIONARY TIME SERIES WITH A SEASONAL COMPONENT OF s = 12 MONTHS.
THE AUTOCORRELATION FUNCTION
DECLINES VERY SLOWLY, AND DOES NOT EXHIBIT CYCLICAL BEHAVIOR. THE ACF SUGGESTS
HOMOGENEOUS NONSTATIONARY BEHAVIOR, SO SIMPLE DIFFERENCING IS APPLIED TO OBTAIN
A STATIONARY TIME SERIES. PLOTS ARE SHOWN OF THE ACFs OF TRANSFORMED DATA
APPLYING SINGLE DIFFERENCES OF TIME SPANS 1 AND 12 AND A DOUBLE DIFFERENCE OF
SPANS 1 AND 12. THAT IS, IF THE ORIGINAL (UNTRANSFORMED) DATA ARE DENOTED AS zt,
THEN THE TRANSFORMED SERIES ARE ![]() ,
, ![]() and
and ![]() .
.
THE SINGLE-DIFFERENCED SERIES ARE NONSTATIONARY, BUT THE DOUBLE-DIFFERENCED SERIES IS STATIONARY.
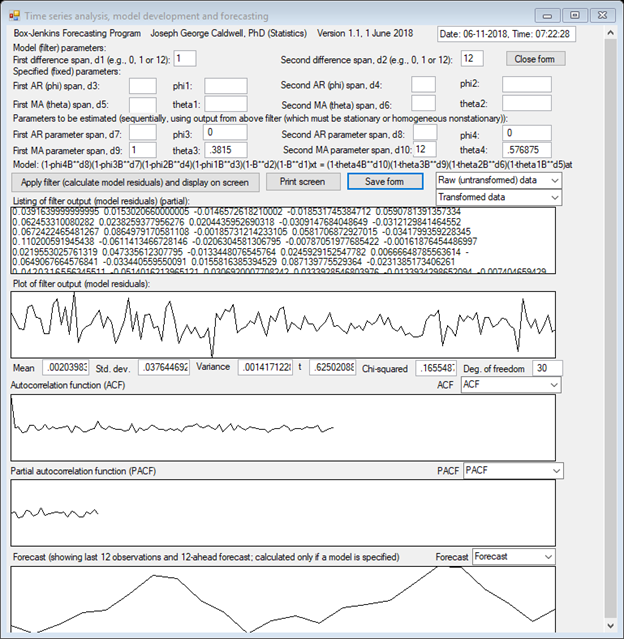
FOR A MODEL INCLUDING A SPAN-1 AND SPAN-12 DIFFERENCING, IT IS ANTICIPATED THAT A REASONABLE MODEL CHOICE MIGHT BE OF ORDER (0,1,1) X (0,1,1)12, THAT IS, A MODEL OF THE FORM
![]()
(SINCE THERE ARE BUT TWO THETA PARAMETERS FOR EACH TIME SPAN, WE SHALL USE THE SIMPLER NOTATION θ = θ12 AND Θ = θ12 IN THE FORMULAS THAT FOLLOW.)
FOR THIS MODEL, THE AUTOCOVARIANCES OF wt ARE:
![]()
![]()
![]()
![]()
![]()
THE EXPRESSIONS FOR γ1 AND γ12 IMPLY
![]()
AND
![]()
FROM THE SAMPLE DATA,
ESTIMATED VALUES OF ρ1 AND ρ12
ARE OBTAINED AS ![]() AND
AND ![]() .
.
SUBSTITUTING THESE VALUES IN THE PRECEDING AND SOLVING FOR θ AND Θ YIELDS THE METHOD-OF-MOMENTS ESTIMATES FOR θ AND Θ.
THE VALUES OF θ AND Θ ARE OBTAINED FROM THE QUADRATIC FORMULA:
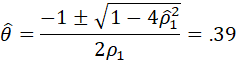
AND

(NOTE THAT THE SOLUTION IS NOT UNIQUE; THE SOLUTION IS TAKEN THAT CORRESPONDS TO ROOTS OF (1 – θB) AND (1 – ΘB) BEING OUTSIDE THE UNIT CIRCLE, I.E., VALUES OF θ AND Θ LESS THAN ONE IN MAGNITUDE.)
THE PRECEDING VALUES –
METHOD-OF-MOMENT ESTIMATES – ARE CONSIDERED “ROUGH” INITIAL VALUES. IMPROVED
VALUES MAY BE OBTAINED BY THE METHOD OF LEAST SQUARES OR, EQUIVALENTLY, BY
MAXIMIZING THE LIKELIHOOD ASSUMING A NORMAL DISTRIBUTION FOR THE MODEL ERROR
TERMS. APPLYING THAT METHOD YIELDS THE VALUES ![]() AND
AND ![]() (THESE VALUES VARY SLIGHTLY FROM THOSE SHOWN IN BJRL,
AND IN STATA BECAUSE SLIGHTLY DIFFERENT NUMERICAL ESTIMATION PROCEDURES ARE
USED.)
(THESE VALUES VARY SLIGHTLY FROM THOSE SHOWN IN BJRL,
AND IN STATA BECAUSE SLIGHTLY DIFFERENT NUMERICAL ESTIMATION PROCEDURES ARE
USED.)
THE ESTIMATED VARIANCE OF THE MODEL RESIDUALS IS
![]()
AND THE ESTIMATED STANDARD DEVIATION OF THE MODEL RESIDUALS IS
![]()
THE MEAN OF THE RESIDUALS IS .00204. THE t VALUE FOR THIS (FOR DEGREES OF FREEDOM = 128) IS .625. THE STANDARD CHI-SQUARE STATISTIC FOR THE FIRST 30 ESTIMATED AUTOCORRELATIONS OF THE RESIDUALS IS .165 (DEGREES OF FREEDOM = 30). THESE STATISTICS SHOW NO EVIDENCE THAT THE MODEL IS INADEQUATE.
THE PROGRAM OUTPUT INCLUDES A PLOT OF THE 12-AHEAD FORECAST FROM THE LAST OBSERVATION.
3. SUMMARY OF MULTIVARIABLE UNIVARIATE MODELS (TRANSFER FUNCTION MODELS, DISTRIBUTED LAG MODELS)
THE PRECEDING DISCUSSION ADDRESSES MODELS IN WHICH THE STOCHASTIC BEHAVIOR OF AN OBSERVED VARIABLE COULD BE DESCRIBED BY THE PROBABILITY DISTRIBUTION OF A SINGLE RANDOM VARIABLE, I.E., THE MODEL ERROR TERM. SUCH MODELS, INVOLVING A SINGLE RANDOM VARIABLE, ARE CALLED UNIVARIATE MODELS. THE MODEL ERROR TERM IS THE SINGLE INPUT TO THE SYSTEM, AND THE OBSERVED RANDOM VARIABLE IS THE SINGLE OUTPUT, DEPENDENT ON THE INPUT. WE NOW TURN TO CONSIDERATION OF MODELS THAT INVOLVE MORE THAN A SINGLE INPUT, BUT STILL JUST A SINGLE OUTPUT.
FOR THIS SITUATION, THE MODEL INPUTS MAY BE DETERMINISTIC VARIABLES OR RANDOM VARIABLES. THE MODEL INPUTS INCLUDE EXPLANATORY VARIABLES AND A MODEL ERROR TERM. THE MODEL OUTPUT IS AN EXPLAINED VARIABLE, DEPENDENT ON THE EXPLANATORY VARIABLES AND THE MODEL ERROR TERM.
THE KEY POINT HERE IS THAT THE ESSENTIAL STOCHASTIC PROPERTIES OF THE TIME SERIES CAN BE DESCRIBED BY A UNIVARIATE DISTRIBUTION OF THE MODEL ERROR TERM. ALTHOUGH A NUMBER OF RANDOM VARIABLES MAY BE PRESENT IN THE MODEL (E.G., THE EXPLANATORY VARIABLES OF A UNIVARIATE MULTIPLE REGRESSION MODEL), IT IS NOT NECESSARY TO USE A JOINT PROBABILITY DISTRIBUTION (OF MORE THAN ONE COMPONENT) TO DESCRIBE THE STOCHASTIC PROPERTIES OF THE SINGLE RESPONSE VARIABLE OF INTEREST.
FOR THIS SECTION, WE SHALL ASSUME THAT THE MODEL EXPLANATORY VARIABLES ARE EXOGENOUS. THERE ARE A NUMBER OF DEFINITIONS OF THE TERM EXOGENOUS. THEY INVOLVE STATEMENTS ABOUT CONDITIONAL DISTRIBUTIONS OR MODEL ERROR TERMS. FOR THE PURPOSE OF ESTIMATING MODEL PARAMETERS, A VARIABLE IS EXOGENOUS IF KNOWLEDGE OF THE PROCESS GENERATING IT CONTAINS NO INFORMATION ABOUT THE PARAMETERS OF THE DISTRIBUTION OF THE MODEL OUTPUT VARIABLE, CONDITIONAL ON THE EXOGENOUS VARIABLE.
THIS DEFINITION OF EXOGENEITY (INTRODUCED BY R. F. ENGLE, D. F. HENDRY, AND J. F. RICHARD IN 1983) RELATES TO THE SPECIFIC ISSUE OF ESTIMATING CERTAIN PARAMETERS. IT DIFFERS FROM THE USUAL (ECONOMETRIC, MODEL-ERROR-BASED) DEFINITION, INVOLVING COVARIANCES BETWEEN MODEL ERROR TERMS AND MODEL EXPLANATORY VARIABLES.
WHETHER THE CONDITIONS HOLD CANNOT BE DETERMINED FROM ANALYSIS OF DATA. (DATA ANALYSIS MIGHT FALSIFY EXOGENEITY, BUT IT CANNOT ESTABLISH IT.) THEY ARE DETERMINED FROM A CAUSAL MODEL.
EXOGENEITY IS ASSUMED BASED ON THEORETICAL CONSIDERATIONS. WHETHER A VARIABLE IS EXOGENOUS (RELATIVE TO ESTIMATION OF ONE OR MORE MODEL PARAMETERS) IS DETERMINED FROM (OR SPECIFIED IN) A CAUSAL MODEL SHOWING THE CAUSAL RELATIONSHIPS AMONG ALL MODEL VARIABLES.
IF THE MODEL RESIDUALS FOR AN EXPLANATORY VARIABLE ARE INDEPENDENT OF THOSE OF THE EXPLAINED VARIABLE, THEN THE EXPLANATORY VARIABLE IS EXOGENOUS. IT WOULD HOLD, FOR EXAMPLE, IF THE EXPLANATORY VARIABLE WERE GENERATED INDEPENDENTLY OF THE EXPLAINED VARIABLE (E.G., AS IN A COMPUTER SIMULATION OR AS INPUT TO A CONTROLLED EXPERIMENT). THE AMOUNT OF RAINFALL IN AN AREA WOULD EXOGENOUS IN ANY MODEL DEALING WITH ECONOMIC QUANTITIES.
AN EXPLANATORY VARIABLE THAT IS STOCHASTICALLY INDEPENDENT OF THE OTHER MODEL VARIABLES IS EXOGENOUS, BUT REQUIRING EXPLANATORY VARIABLES TO BE INDEPENDENT IS A STRONGER CONDITION THAN IS NECESSARY. THE CONCEPTS OF EXOGENEITY ARE WEAKER THAN INDEPENDENCE.
FOR ADDITIONAL DISCUSSION OF EXOGENEITY, SEE THE FOLLOWING REFERENCES:
BANERJEE, ANINDYA, JUAN DOLADO, JOHN W. GALBRAITH AND DAVID F. HENDRY, CO-INTEGRATION, ERROR CORRECTION, AND THE ECONOMETRIC ANALYSIS OF NON-STATIONARY DATA, OXFORD UNIVERSITY PRESS, 1993
JUDEA PEARL, CAUSALITY: MODELS, REASONING, AND INFERENCE, 2nd ED (CAMBRIDGE UNIVERSITY PRESS, 2009).
HERE FOLLOWS SOME ADDITIONAL INFORMATION ABOUT EXOGENEITY.
ENGLE ET AL. INTRODUCE THREE DIFFERENT LEVELS OF EXOGENEITY, CORRESPONDING TO DIFFERENT ESTIMATION PROBLEMS: INFERENCE, FORECASTING CONDITIONAL ON FORECASTS OF THE EXOGENOUS VARIABLES, AND POLICY ANALYSIS. THESE LEVELS ARE WEAK EXOGENEITY, STRONG EXOGENEITY AND SUPER EXOGENEITY. THE DEFINITIONS OF THESE EXOGENEITY CONCEPTS ARE PRESENTED ON PAGE 18 OF BANERJEE OP. CIT. THEY CORRESPOND TO CONDITIONS ON THE DISTRIBUTION FUNCTIONS INVOLVED IN THE PROBLEM. IF WEAK EXOGENEITY HOLDS, THEN THE MODEL PARAMETERS ARE ESTIMABLE. IF STRONG EXOGENITY HOLDS, THEN FORECASTS MAY BE ESTIMATED CONDITIONAL ON FORECASTED VALUES OF THE EXOGENOUS VARIABLES, ASSUMING THAT THEIR DISTRIBUTION IS UNCHANGED. IF SUPER EXOGENEITY HOLDS, THEN FORECASTS MAY BE MADE CONDITIONAL ON CHANGES IN THE PARAMETERS OF THE DISTRIBUTION OF THE EXOGENOUS VARIABLES.
ENGLE’S CONDITIONS ARE EXPRSSED IN TERMS OF CONDITIONAL DISTRIBUTIONS. THE CONDITIONS ARE COMPLICATED. IT WOULD APPEAR THAT ESTABLISHING EXOGENEITY BY DIRECTLY ESTABLISHING THE VERITY OF THESE CONDITIONS WOULD BE DIFFICULT. A MORE STRAIGHTFORWARD APPROACH WOULD BE TO CONSTRUCT A CAUSAL MODEL DIAGRAM (A DIRECTED ACYCLIC GRAPH) SHOWING THE CAUSAL RELATIONSHIPS AMONG THE MODEL VARIABLES, AND ESTABLISHING WHETHER JUDEA PEARL’S ESTIMABILITY CONDITIONS HELD FOR ESTIMATES OF INTEREST.
BANERJEE (OP. CIT. P 19) COMPARES THE PRECEDING THREE DEFINITIONS OF EXOGENEITY TO THE STANDARD ONES USED IN ECONOMETRIC ANALYSIS: STRICT EXOGENEITY AND PREDETERMINEDNESS. IF ut IS THE MODEL ERROR TERM, THEN A VARIABLE zt IS STRICTLY EXOGENOUS IF E[ztut+i] = 0 FOR ALL i, AND IS PREDETERMINED IF E[ztut+i] = 0 FOR ALL i>=0. ENGLE SHOWS THAT THESE CONDITIONS ARE NEITHER NECESSARY NOR SUFFICIENT FOR VALID INFERENCE, SINCE THEY DO NOT RELATE TO PARAMETERS OF INTEREST.
AMBIGUITY OF THE TERM “MULTIVARIATE”
IT IS RECOGNIZED THAT A UNIVARIATE MODEL CONTAINING EXPLANATORY VARIABLES MAY BE REFERRED TO AS A “MULTIVARIATE” MODEL. IN THE UNIVARIATE MODEL JUST DESCRIBED, THE OUTPUT VARIABLE AND THE EXPLANATORY VARIABLES MAY ALL BE RANDOM VARIABLES, AND THE MODEL COULD REASONABLY BE REFERRED TO AS A MULTIVARIATE MODEL. IN THE CASE IN WHICH THERE IS A SINGLE OUTPUT VARIABLE AND THE EXPLANATORY VARIABLES ARE EXOGENOUS, HOWEVER, SOME OF THE CONCEPTS ARE SIMPLER THAN FOR THE GENERAL MULTIVARIATE CASE (OF MORE THAN ONE OUTPUT VARIABLE). FOR THIS REASON, AND BECAUSE THE UNIVARIATE MODEL IS AN IMPORTANT SPECIAL CASE, IT IS ADDRESSED IN A SEPARATE SECTION.
(IN THIS PRESENTATION, THE TERM “MULTIVARIATE” WILL BE USED TO REFER TO A SITUATION IN WHICH THE PROBABILITY DISTRIBUTION OF INTEREST IS A NON-DEGENERATE (NON-TRIVIAL) ONE, OF DIMENSION GREATER THAN ONE, IN WHICH THE PROBABILITY MASS OCCURS IN MORE THAN ONE DIMENSION. IF THE PROBABILITY DISTRIBUTION OF INTEREST IS ONE-DIMENSIONAL, THEN THE TERM “UNIVARIATE” WILL BE USED. FOR EXAMPLE, A REGRESSION MODEL IN WHICH THERE IS A SINGLE DEPENDENT (EXPLAINED, RESPONSE, OUTPUT) VARIABLE AND SEVERAL EXPLANATORY VARIABLES (WHICH MAY OR MAY NOT BE RANDOM VARIABLES, BUT WHICH ARE NOT CORRELATED WITH THE MODEL ERROR TERM) IS A UNIVARIATE MODEL. SOME AUTHORS SAY THAT A MULTIVARIATE SITUATION IS ONE IN WHICH THE RANDOM VARIABLES OF THE MODEL ARE INTERRELATED. THIS DEFINITION DOES NOT WORK HERE, SINCE IN A REGRESSION MODEL THE DEPENDENT VARIABLE AND THE EXPLANATORY VARIABLES ARE INTERRELATED, BUT A UNIVARIATE PROBABILITY DISTRIBUTION SUFFICES TO DESCRIBE THE ESSENCE OF THE SITUATION. WE REFER TO A UNIVARIATE MODEL INVOLVING EXPLANATORY VARIABLES AS A “MULTIVARIABLE” MODEL (NOT A “MULTIVARIATE” ONE) OR A “MULTIVARIABLE UNIVARIATE” MODEL.)
THE TERM “MULTIPLE TIME SERIES” MAY REFER EITHER TO THE CASE OF A UNIVARIATE MODEL WITH EXPLANATORY VARIATES, OR TO A GENERAL MULTIVARIATE MODEL (AND USUALLY TO THE LATTER).
USING THE STANDARD METHODS OF ESTIMATION, SUCH AS LEAST SQUARES OR MAXIMUM LIKELIHOOD FOR A NORMAL DISTRIBUTION, THE NUMERICAL VALUES OF ESTIMATES OF INTEREST ARE THE SAME, WHETHER THE MODEL IS UNIVARIATE MODEL WITH EXOGENOUS EXPLANATORY VARIABLES, OR A GENERAL MULTIVARIATE MODEL. WHAT DIFFERS IS THE INTERPRETATION OF VARIOUS QUANTITIES, AND THEIR SAMPLING DISTRIBUTIONS (AND RELATED QUANTITIES, SUCH AS PROPERTIES OF TESTS OF HYPOTHESES AND CONFIDENCE INTERVALS). FOR EXAMPLE, IF THE EXPLANATORY VARIABLE IN A UNIVARIATE MODEL IS A RANDOM VARIABLE, THEN IT MAKES SENSE TO REFER TO THE COVARIANCE OF THAT VARIABLE WITH OTHER VARIABLES, AND A SUM OF CROSS PRODUCTS IS AN ESTIMATOR OF THE COVARIANCE, AND IT HAS A SAMPLING DISTRIBUTION. OTHERWISE, IT IS SIMPLY A SUM OF CROSS PRODUCTS (NOT AN ESTIMATE OF A DISTRIBUTION PARAMETER OR MOMENT). FOR SIMPLICITY OF EXPOSITION, A SUM OF CROSS PRODUCTS MAY BE REFERRED TO AS A COVARIANCE, WHETHER IT INVOLVES RANDOM VARIABLES OR NOT.
UNIVARIATE TIME SERIES MODELS WITH EXOGENOUS VARIABLES ARE VARIOUSLY REFERRED TO AS TRANSFER-FUNCTION MODELS OR DISTRIBUTED-LAG MODELS OR MODELS WITH EXOGENOUS VARIABLES. THE TERM “TRANSFER FUNCTION” IS USUALLY USED IN ENGINEERING APPLICATIONS AND THE TERM “DISTRIBUTED LAG” IN ECONOMIC APPLICATIONS. WE SHALL USE THE TERM “TRANSFER FUNCTION.”
UNIVARIATE BOX-JENKINS TYPE MODELS CONTAINING EXOGENOUS EXPLANATORY VARIABLES ARE SOMETIMES REFERRED TO AS ARIMAX MODELS (ARIMA PLUS “X” FOR EXOGENOUS).
TO SIMPLIFY THIS PRESENTATION, WE SHALL IN THIS SECTION SUMMARIZE SOME FEATURES OF MULTIVARIABLE UNIVARIATE TIME SERIES MODELS, BUT DEFER DETAILED DISCUSSION OF IDENTIFICATION AND ESTIMATION PROCEDURES TO THE GENERAL MULTIVARIATE CASE. TRANSFER FUNCTION MODELS MAY BE REPRESENTED AS SPECIAL CASES OF GENERAL MULTIVARIATE MODELS; THIS WILL BE DISCUSSED IN THE SECTION ON MULTIVARIATE MODELS.
THE RELATIONSHIP OF TRANSFER FUNCTION MODELS TO GENERAL MULTIVARIATE MODELS IS SOMEWHAT ANALOGOUS TO THE SITUATION IN ANALYSIS OF VARIANCE OR REGRESSION ANALYSIS, WHERE THE EXPLANATORY VARIABLES (“EFFECTS”) OF A MODEL MAY BE FIXED OR RANDOM. THE ESTIMATES OF THE EFFECTS ARE THE SAME IN EITHER CASE, BUT THE DISTRIBUTIONAL CHARACTERISTICS (AND TESTS OF HYPOTHESES AND CONFIDENCE INTERVALS) DIFFER. IN ENGINEERING APPLICATIONS, IT IS OFTEN POSSIBLE TO CONTROL THE LEVELS OF EXPLANATORY VARIABLES, AS IN A DESIGNED LABORATORY EXPERIMENT OR TESTING OF AN ELECTRONIC FILTER. IN SUCH APPLICATIONS, THE EXPLANATORY VARIABLE MAY OR MAY NOT BE A RANDOM VARIABLE. IN ECONOMIC APPLICATIONS, MANY VARIABLES MAY BE OBSERVED, BUT FEW ARE CONTROLLED. IN ECONOMIC APPLICATIONS, ATTENTION HENCE FOCUSES ON THE CASE IN WHICH THE EXPLANATORY VARIABLES ARE RANDOM VARIABLES. (IF THEY ARE FIXED, THEN THERE IS NO CORRELATION BETWEEN THEM AND THE MODEL ERROR TERM, AND THE LEAST-SQUARES PROCEDURE PRODUCES UNBIASED ESTIMATES. IF THEY ARE RANDOM, IT IS ESSENTIAL THAT THEY NOT BE CORRELATED WITH THE MODEL ERROR TERMS, OR ELSE THE PARAMETER ESTIMATES MAY BE BIASED.)
A DISCRETE LINEAR TRANSFER FUNCTION MODEL
THE FOLLOWING IS A REPRESENTATION OF A GENERAL CLASS OF TRANSFER-FUNCTION MODELS. SEE BJRL FOR DETAILS.
SUPPOSE THAT THE SYSTEM OUTPUT, Yt, IS RELATED TO THE SYSTEM INPUT, Xt, BY THE EQUATION
![]()
OR
![]()
WHERE THE MODEL ERROR TERM, Nt, IS INDEPENDENT OF THE INPUT, Xt. IT MAY BE FURTHER ASSUMED THAT THE MODEL ERROR TERM (OR NOISE) MAY BE REPRESENTED BY AN ARIMA PROCESS:
![]()
WHERE at IS A WHITE NOISE SEQUENCE.
IN GENERAL, THE INPUT Xt MAY BE ANY SEQUENCE OF NUMBERS, E.G., LEVELS IN A DESIGNED EXPERIMENT, OR A SINE WAVE. FOR THIS PRESENTATION, WE SHALL ASSUME, UNLESS OTHERWISE STATED, THAT THE INPUT Xt IS A STOCHASTIC PROCESS.
THE OPERATOR
![]()
IS CALLED THE TRANSFER FUNCTION OF THE PROCESS. THE WEIGHTS ν0, ν1, … ARE CALLED THE IMPULSE RESPONSE FUNCTION OF THE PROCESS.
NOTE THAT IT IS NOT REASONABLE TO PARAMETERIZE THE PROCESS IN TERMS OF THE ν’s. IN GENERAL, THAT WOULD BE A VERY NON-PARSIMONIOUS REPRESENTATION. FOR MANY PROCESSES THAT ARE REPRESENTED BY A SMALL NUMBER OF PARAMETERS (φs AND θs), THE ν’s ARE FUNCTIONALLY RELATED. ESTIMATES OF A LARGE NUMBER OF FUNCTIONALLY RELATED PARAMETERS (CONSIDERED FUNCTIONALLY INDEPENDENT) WOULD BE INEFFICIENT AND UNSTABLE.
IF THE INPUT Xt IS HELD INDEFINITELY AT THE VALUE OF ONE, Yt EVENTUALLY ATTAINS THE VALUE
![]()
WHICH IS CALLED THE STEADY-STATE GAIN OF THE PROCESS.
FOR STABILITY OF THE PROCESS, IT IS REQUIRED THAT THE ROOTS OF THE POLYNOMIAL δ(B) = 0 LIE OUTSIDE THE UNIT CIRCLE. (THIS IS EQUIVALENT TO REQUIRING THAT THE SERIES v(B) CONVERGE FOR |B|≤1.) WE SHALL ASSUME THAT THIS CONDITION HOLDS.
FEATURES OF TRANSFER FUNCTION MODELS.
IMPULSE RESPONSE AND STEP RESPONSE FUNCTIONS
JUST AS ARIMA PROCESSES WERE CHARACTERIZED BY THEIR AUTOCORRELATION AND PARTIAL AUTOCORRELATION FUNCTIONS, TRANSFER FUNCTIONS ARE CHARACTERIZED BY THEIR RESPONSE TO IMPULSE AND STEP INPUTS.
AN IMPULSE INPUT IS DEFINED AS AN INPUT X0 = 1 and Xt = 0 FOR t ≠ 0. THE RESPONSES TO THIS INPUT ARE GIVEN BY THE IMPULSE RESPONSE FUNCTION.
A STEP INPUT IS DEFINED AS AN INPUT OF Xt = 1 IF t ≥ 0 AND Xt =0 IF t < 0. THE RESPONSE OF THE SYSTEM TO A STEP INPUT IS CALLED THE STEP RESPONSE FUNCTION.
FOR A SPECIFIED (TRUE, THEORETICAL, POPULATION) MODEL, THE IMPULSE RESPONSE FUNCTION AND THE STEP RESPONSE FUNCTIONS MAY BE DERIVED.
[INSERT EXAMPLE OF IMPULSE RESPONSE FUNCTION AND STEP RESPONSE FUNCTION.]
CROSS-COVARIANCE AND CROSS-CORRELATION FUNCTIONS
A STATIONARY UNIVARIATE TIME SERIES IS CHARACTERIZED BY THE MEAN, VARIANCE, AND AUTOCOVARIANCE (OR AUTOCORRELATION) FUNCTIONS. SIMILARLY, STATIONARY MULTIVARIATE TIME SERIES (VECTOR STOCHASTIC PROCESSES) ARE CHARACTERIZED BY THE MEANS, VARIANCES AND COVARIANCES OF THE COMPONENT RANDOM VARIABLES. (THE TERM “COMPONENT” REFERS TO ONE OF THE COMPONENTS OF THE MULTIVARIATE RESPONSE VECTOR.)
FOR EASE OF DISCUSSION, WE SHALL RESTRICT DISCUSSION TO THE BIVARIATE CASE, IN WHICH THERE IS A SINGLE EXOGENOUS VARIATE, Xt, AND A SINGLE RESPONSE (OUTPUT) VARIABLE, Yt. (RECALL THAT WE ARE ASSUMING, UNLESS OTHERWISE STATED, THAT Xt IS A STOCHASTIC PROCESS.) WE SHALL ASSUME THAT THESE PROCESSES ARE STATIONARY. IN THIS CASE, THE (STATIONARY) BIVARIATE TIME SERIES IS CHARACTERIZED BY THE MEANS µx AND µy, VARIANCES σ2x AND σ2y, THE COVARIANCE FUNCTION DEFINED BY
![]()
![]()
AND THE CROSS-COVARIANCE FUNCTIONS DEFINED BY
![]()
![]()
FOR A STATIONARY SERIES, THE CROSS-COVARIANCE FUNCTIONS ARE THE SAME FOR ALL t.
IN GENERAL, ![]() IS NOT EQUAL TO
IS NOT EQUAL TO ![]() .
.
SINCE
![]()
IT SUFFICES TO DEFINE JUST
ONE CROSS-COVARIANCE FUNCTION ![]() FOR k = 0,
FOR k = 0, ![]()
THE QUANTITY
![]()
IS CALLED THE CROSS-CORRELATION COEFFICIENT AT LAG k, AND THE FUNCTION
![]()
IS CALLED THE CROSS-CORRELATION FUNCTION (CCF) OF THE STATIONARY BIVARIATE PROCESS.
AS MENTIONED, IT IS ASSUMED IN THIS SECTION THAT THE TWO SERIES (Xt AND Yt) ARE STATIONARY. IF THE TWO SERIES ARE NOT STATIONARY, THERE ARE TWO ALTERNATIVE WAYS OF TRANSFORMING TO STATIONARITY. THE FIRST IS TO APPLY DIFFERENCING TO EACH SERIES, AS WAS DONE IN THE CASE OF A SINGLE TIME SERIES. A SECOND POSSIBILITY IS THAT A LINEAR COMBINATION OF THE COMPONENT RANDOM VARIABLES MAY BE OF A LOWER ORDER OF INTEGRATION THAN THE ORIGINAL SERIES (I.E., LESS DIFFERENCING IS REQUIRED TO ACHIEVE STATIONARITY), SO THAT LESS DIFFERENCING IS REQUIRED TO TRANSFORM THAT COMBINATION TO STATIONARITY THAN IS REQUIRED FOR THE ORIGINAL SERIES. IF THIS HAPPENS, THE VARIABLES ARE SAID TO BE COINTEGRATED. THAT POSSIBILITY IS UNLIKELY IN THE CASE IN WHICH THE EXPLANATORY VARIABLES ARE EXOGENOUS, AND SO IT WILL NOT BE ADDRESSED IN THIS SECTION. THE ISSUE OF COINTEGRATION IS ADDRESSED IN THE SECTION DEALING WITH MULTIVARIATE VARIABLES THAT ARE NOT EXOGENOUS. FOR THIS SECTION, IT WILL BE ASSUMED THAT THE VARIABLES ARE NOT COINTEGRATED. IN THIS CASE, IF THEY ARE NONSTATIONARY, THEY ARE TRANSFORMED TO STATIONARITY BY DIFFERENCING. IF DIFFERENCING IS DONE, THEN ZERO-ROOT FACTORS ARE ADDED TO THE MODEL FORMULA GIVEN ABOVE.
A POTENTIAL PROBLEM WITH DIFFERENCING IN THE CASE OF A MODEL WITH EXPLANATORY VARIABLES IS THAT IT REMOVES INFORMATION ABOUT VARIABLE LEVELS. IF THE RELATIONSHIP BETWEEN THE VARIABLES INVOLVES THE LEVELS OF THE VARIABLES, THEN DIFFERENCING WOULD RESULT IN A MISSPECIFIED MODEL. (AS AN EXAMPLE, CONSIDER THE EFFECT OF RAINFALL AMOUNT ON CROP YIELD. THE CROP YIELD DEPENDS ON THE CUMULATIVE RAINFALL AMOUNT, NOT ON SHORT-TERM FLUCTUATIONS. RAINFALL AND CUMULATIVE RAINFALL ARE NONSTATIONARY. IF DIFFERENCING WERE APPLIED TO ACHIEVE STATIONARITY, INFORMATION ABOUT THE RELATIONSHIP OF YIELD TO RAINFALL AMOUNT WOULD BE LOST.)
ESTIMATION OF THE CROSS-COVARIANCE AND CROSS-CORRELATION FUNCTIONS
LET US ASSUME THAT THE TWO SERIES (Xt AND Yt) ARE STATIONARY (OR THAT DIFFERENCING HAS BEEN APPLIED TO ACHIEVE STATIONARITY). AN ESTIMATE OF THE CROSS-COVARIANCE COEFFICIENT AT LAG k IS
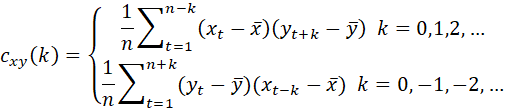
WHERE ![]() AND
AND ![]() DENOTE THE MEANS OF THE xt AND yt
SERIES. THE ESTIMATE rxy(k) OF THE CROSS-CORRELATION COEFFICIENT ρxy(k) AT LAG k ARE OBTAINED BY SUBSTITUTING
DENOTE THE MEANS OF THE xt AND yt
SERIES. THE ESTIMATE rxy(k) OF THE CROSS-CORRELATION COEFFICIENT ρxy(k) AT LAG k ARE OBTAINED BY SUBSTITUTING ![]() FOR
FOR ![]() , sx2 = cxx(0) for σx2, and sy2 = cyy(0)
for σy2 IN THE
EXPRESSION FOR
, sx2 = cxx(0) for σx2, and sy2 = cyy(0)
for σy2 IN THE
EXPRESSION FOR ![]() . THIS YIELDS:
. THIS YIELDS:
![]()
BJRL DISCUSS THE BEHAVIOR OF THE CROSS-CORRELATION FUNCTIONS AS A FUNCTION OF THE MODEL STRUCTURAL PARAMETERS (r, s, and b). THIS BEHAVIOR MAY BE USED AS A GUIDE IN SUGGESTING A MODEL STRUCTURE THAT MAY REPRESENT THE UNDERLYING PROCESS WELL.
FOR A STATIONARY PROCESS, THE AUTOCORRELATION AND CROSS-CORRELATION FUNCTIONS DIE OUT QUICKLY. IF THE OBSERVED DATA EXHIBIT NONSTATIONARY BEHAVIOR, THE SERIES ARE TRANSFORMED BY DIFFERENCING TO ACHIEVE STATIONARITY. (IT IS ASSUMED HERE THAT THE SERIES ARE NOT COINTEGRATED.)
IDENTIFICATION OF TRANSFER-FUNCTION MODELS, USING THE CROSS-CORRELATION FUNCTION; PREWHITENING
THE COVARIANCES ![]() OF THE ESTIMATES
OF THE ESTIMATES
![]() DEPEND ON THE CROSS CORRELATIONS
DEPEND ON THE CROSS CORRELATIONS ![]() , AND IF THESE ARE SUBSTANTIAL, THEN THE COVARIANCES
ARE LARGE. FOR THIS REASON, EXAMINATION OF THE ESTIMATED CROSS-CORRELATION
FUNCTION OF THE OUTPUT (yt) AND INPUT (xt) SERIES IS NOT
VERY HELPFUL IN ASSISTING IDENTIFICATION OF A USEFUL MODEL REPRESENTATION.
, AND IF THESE ARE SUBSTANTIAL, THEN THE COVARIANCES
ARE LARGE. FOR THIS REASON, EXAMINATION OF THE ESTIMATED CROSS-CORRELATION
FUNCTION OF THE OUTPUT (yt) AND INPUT (xt) SERIES IS NOT
VERY HELPFUL IN ASSISTING IDENTIFICATION OF A USEFUL MODEL REPRESENTATION.
EVEN UNDER THE HYPOTHESIS THAT THE TWO PROCESSES HAVE ZERO CROSS-CORRELATION, THE COVARIANCES ARE SUBSTANTIAL. IF THE TWO PROCESSES HAVE ZERO CROSS-CORRELATION AND ONE OF THEM IS A WHITE NOISE PROCESS, HOWEVER, THEN THE AUTOCORRELATION FUNCTION OF THE ESTIMATED CROSS CORRELATIONS IS THE SAME AS THE AUTOCORRELATION FUNCTION OF THE OUTPUT yk.
IN THIS CASE, EXAMINATION OF THE CROSS-CORRELATION FUNCTION OF THE MODEL RESIDUALS CAN BE A USEFUL INDICATOR OF THE GOODNESS OF FIT OF A TENTATIVE MODEL. THIS FACT PROVIDES A USEFUL MEANS OF TESTING THE ADEQUACY OF A FITTED BIVARIATE TRANSFER FUNCTION MODEL.
WE ASSUME THAT THE PROCESS MAY BE REPRESENTED BY THE FOLLOWING TRANSFER-FUNCTION MODEL:
![]()
WHERE THE NOISE PROCESS Nt MAY BE REPRESENTED BY AN ARIMA PROCESS THAT IS STOCHASTICALLY INDEPENDENT OF Xt.
AFTER DIFFERENCING (TO ACHIEVE STATIONARITY OF THE Yt SERIES), THE FOLLOWING MODEL IS ASSUMED:
![]()
FOR SIMPLICITY, LET US
DENOTE THE OPERATOR ![]() BY
BY ![]()
LET US CONSIDER THE CASE IN WHICH THE Xt SERIES MAY BE ADEQUATELY REPRESENTED BY THE FOLLOWING MODEL:
![]()
WHERE αt IS A WHITE NOISE PROCESS.
LET US APPLY THE TRANSFORMATION OF THE MODEL FOR xt TO THE OUTPUT SERIES yt:
![]()
THE THUS-TRANSFORMED
VARIATE ![]() IS CALLED A PREWHITENED SERIES. (THIS TERM IS
A MISNOMVER AND IS MISLEADING; APPLYING THE TRANSFORMATION TO THE Xt
SERIES WOULD “WHITEN” IT, BUT APPLYING THE TRANSFORMATION TO THE OUTPUT SERIES
Yt DOES NOT “WHITEN” IT.) THE MODEL FOR THIS TRANFORMED VARIABLE IS
IS CALLED A PREWHITENED SERIES. (THIS TERM IS
A MISNOMVER AND IS MISLEADING; APPLYING THE TRANSFORMATION TO THE Xt
SERIES WOULD “WHITEN” IT, BUT APPLYING THE TRANSFORMATION TO THE OUTPUT SERIES
Yt DOES NOT “WHITEN” IT.) THE MODEL FOR THIS TRANFORMED VARIABLE IS
![]()
WHERE
![]()
MULTIPLYING BOTH SIDES OF THE TRANSFORMED MODEL
![]()
BY αt AND TAKING EXPECTATIONS YIELDS
![]()
WHERE ![]() IS THE CROSS-COVARIANCE FUNCTION OF THE SERIES αt AND βt. IN
TERMS OF THE CROSS-CORRELATION FUNCTION, THIS IS
IS THE CROSS-COVARIANCE FUNCTION OF THE SERIES αt AND βt. IN
TERMS OF THE CROSS-CORRELATION FUNCTION, THIS IS
![]()
THAT IS, THE ESTIMATED CROSS-CORRELATION FUNCTION OF THE PREWHITENED Yt AND Xt SERIES IS THE TRANSFER FUNCTION FOR THE TRANSFORMED MODEL.
THE CROSS-CORRELATION
FUNCTION ![]() IS UNKNOWN, AND
IS UNKNOWN, AND ![]() IS ESTIMATED BY:
IS ESTIMATED BY:
![]()
UNDER THE ASSUMPTION THAT αt AND βt ARE NOT CROSS-CORRELATED, THE VARIANCE OF THE CROSS CORRELATIONS IS
![]()
THE PRECEDING RESULTS SHOW THAT BY PREWHITENING, THE CROSS-CORRELATION FUNCTION IS A USEFUL GUIDE TO SUGGESTING THE FORM OF THE POLYNOMIAL v(B), AND HENCE TO SUGGESTING FORMS FOR δ(B) AND ω(B).
ESTIMATION OF PARAMETERS OF TRANSFER-FUNCTION MODELS
THE STANDARD PROCEDURE FOR ESTIMATING THE PARAMETERS OF A TRANSFER-FUNCTION MODEL ARE DESRIBED IN DETAIL IN THE TIMES MANUAL AND IN THE BJRL BOOK.
IT IS EMPHASIZED THAT A CRITICAL ASSUMPTION IN THE MODEL IS THAT THE EXOGENOUS VARIABLE AND THE MODEL ERROR TERM ARE UNCORRELATED (THAT IS, EXOGENOUS). IT THIS ASSUMPTION DOES NOT HOLD, THEN THE ESTIMATES MAY BE BIASED AND INCONSISTENT.
IN APPLICATIONS IN WHICH THE INPUT VARIABLE xt IS CONTROLLABLE, THIS ASSUMPTION MAY BE GUARANTEED BY INDEPENDENTLY GENERATING THE xt SERIES. IN OTHER SITUATIONS, IT MAY BE OBVIOUS THAT THE EXOGENOUS VARIATE IS INDEPENDENT (E.G., WEATHER TEMPERATURE OR RAINFALL AMOUNTS).
SPURIOUS CORRELATIONS
THE PRECEDING DISCUSSION ADDRESSES THE ISSUE OF MODEL IDENTIFICATION UNDER THE ASSUMPTION THAT THE DATA ARE TRANSFORMED TO STATIONARY VARIATES. THE DESCRIBED PROCEDURES CANNOT BE USEFULLY APPLIED TO NONSTATIONARY DATA. IF THE VARIABLES Yt AND Xt ARE NONSTATIONARY, THE LEAST-SQUARES ESTIMATES OF THE TRANSFER-FUNCTION PARAMETERS MAY BE INCONSISTENT – THAT IS, NO MATTER HOW LARGE THE SAMPLE, THE ESTIMATES DO NOT CONVERGE TO THE CORRECT VALUES. THIS SITUATION MAY OCCUR EVEN IF THE SERIES ARE UNRELATED. THIS SITUATION HOLDS, FOR EXAMPLE, IF THE MODEL IS
![]()
WHERE yt, xt,
AND ![]() ARE NONSTATIONARY. THE PROBLEM IS THAT THERE ARE NO
VALUES OF α AND γ FOR WHICH THE ERROR TERM ut IS STATIONARY.
HENCE, THE REQUIREMENT FOR LEAST-SQUARES ESTIMATION THAT THE MODEL ERROR TERM
BE UNCORRELATED (OR, AT LEAST, STATIONARY AND OF KNOWN COVARIANCE STRUCTURE)
AND UNCORRELATED WITH THE MODEL EXPLANATORY VARIABLES IS NOT SATISFIED.
ARE NONSTATIONARY. THE PROBLEM IS THAT THERE ARE NO
VALUES OF α AND γ FOR WHICH THE ERROR TERM ut IS STATIONARY.
HENCE, THE REQUIREMENT FOR LEAST-SQUARES ESTIMATION THAT THE MODEL ERROR TERM
BE UNCORRELATED (OR, AT LEAST, STATIONARY AND OF KNOWN COVARIANCE STRUCTURE)
AND UNCORRELATED WITH THE MODEL EXPLANATORY VARIABLES IS NOT SATISFIED.
THE DIFFICULTY IN ESTIMATING MODEL PARAMETERS WHEN THE TWO VARIABLES ARE NONSTATIONARY IS CALLED THE PROBLEM OF SPURIOUS CORRELATION OR SPURIOUS REGRESSION.
THE PROBLEM OF SPURIOUS CORRELATION / SPURIOUS REGRESSION HAS BEEN RECOGNIZED FOR A LONG TIME, AND WAS FIRST DISCUSSED IN DETAIL BY YULE IN 1926. THIS PROBLEM ARISES WITH HOMOGENEOUS NONSTATIONARY SERIES SINCE THE LEVEL WANDERS ABOUT. FOR A FINITE SAMPLE THE SERIES MAY EXHIBIT TRENDS, WHICH ARE NOT REAL, BUT JUST STATISTICAL ARTIFACTS. IN THIS SITUATION, REGRESSING ONE NONSTATIONARY SERIES ON ANOTHER WILL APPEAR (EVEN IF BOTH SERIES ARE TOTALLY UNRELATED TO EACH OTHER) TO EXHIBIT A RELATIONSHIP THAT APPEARS HIGHLY STATISTICALLY SIGNIFICANT IF STANDARD t AND F TESTS ARE USED TO ASSESS SIGNIFICANCE, BUT IN REALITY IS OF NO SIGNIFICANCE WHATEVER. (THE REASON FOR THIS SITUATION IS THAT THE STANDARD TESTS ASSUME THAT THE OBSERVATIONS ARE INDEPENDENT. IF THEY ARE NONSTATIONARY, THEY ARE NOT INDEPENDENT. FOR A NONSTATIONARY TIME SERIES, NEARBY OBSERVATIONS ARE USUALLY HIGHLY CORRELATED, SO THAT THE AMOUNT OF INFORMATION IN THE SAMPLE IS MUCH LESS THAN FOR A RANDOM SAMPLE OF THE SAME NUMBER OF OBSERVATIONS.)
THERE ARE THREE APPROACHES TO AVOID THE PROBLEM OF SPURIOUS REGRESSION. (SEE HAMILTON OP. CIT. FOR DISCUSSION.) THE FIRST IS TO INCLUDE LAGGED VALUES FOR BOTH THE DEPENDENT AND INDEPENDENT VARIABLES IN THE MODEL. IN THIS CASE THE MODEL BECOMES
![]()
THIS MODEL AVOIDS THE PROBLEM BECAUSE THERE EXIST VALUES OF φ, γ AND δ (E.G., φ = 1, γ = δ = 0) FOR WHICH THE ERROR TERM IS STATIONARY.
THE SECOND APPROACH TO
AVOIDING THE PROBLEM OF SPURIOUS REGRESSION IS TO TRANSFORM TO STATIONARITY BY
DIFFERENCING. SUPPOSE THAT THE VARIABLES ![]() yt AND
yt AND ![]() xt ARE STATIONARY (WHERE
xt ARE STATIONARY (WHERE ![]() ). THEN, AFTER
TRANSFORMING THE ORIGINAL SERIES, THE MODEL
BECOMES
). THEN, AFTER
TRANSFORMING THE ORIGINAL SERIES, THE MODEL
BECOMES
![]()
IN THIS CASE ALL MODEL
VARIABLES ![]() yt,
yt, ![]() xt AND ut ARE STATIONARY, AND
THE PROBLEM OF SPURIOUS REGRESSION DOES NOT EXIST.
xt AND ut ARE STATIONARY, AND
THE PROBLEM OF SPURIOUS REGRESSION DOES NOT EXIST.
THE THIRD APPROACH IS TO ESTIMATE THE MODEL WITH COCHRANE-ORCUTT ADJUSTMENT OF THE RESIDUALS (I.E., REPRESENTING THE MODEL ERROR TERMS AS A FIRST-ORDER AR PROCESS).
TO AVOID THE PROBLEM OF SPURIOUS REGRESSION, IT IS A STANDARD PROCEDURE TO TRANSFORM THE SERIES TO STATIONARITY BY DIFFERENCING. WHILE THIS APPROACH IS OFTEN APPROPRIATE, IT IS TOTALLY INAPPROPRIATE IN TWO SITUATIONS. FIRST, IF THE SERIES ARE IN FACT STATIONARY (E.G., THEY ARE REPRESENTED BY AR MODELS FOR WHICH THE ROOTS OF THE AR POLYNOMIAL ARE NEAR THE UNIT CIRCLE BUT ACTUALLY OUTSIDE IT, SUCH AS AN AR MODEL WITH φ1 = .9). IN THIS CASE DIFFERENCING WILL RESULT IN A MISSPECIFIED MODEL.
THE SECOND SITUATION IN
WHICH DIFFERENCING OF SERIES IS INAPPROPRIATE IS THE FOLLOWING. WE CONSIDER
THE BIVARIATE CASE, IN WHICH THERE IS A SINGLE DEPENDENT VARIABLE yt
AND A SINGLE EXPLANATORY VARIABLE xt. SUPPOSE THAT THE SERIES ARE
NONSTATIONARY BUT CAN BE TRANSFORMED TO STATIONARITY BY DIFFERENCING d TIMES.
IN THIS CASE, THE SERIES ARE SAID TO BE INTEGRATED OF ORDER d. FURTHER,
SUPPOSE THAT THERE EXISTS A LINEAR COMBINATION OF yt AND xt
THAT IS INTEGRATED OF ORDER LESS THAN d. (FOR EXAMPLE, SUPPOSE THAT yt
AND xt ARE NONSTATIONARY, BUT ![]() yt,
yt, ![]() xt AND yt – βxt ARE STATIONARY,
FOR SOME VALUE OF β NOT EQUAL TO ONE IN MAGNITUDE.) IN THIS CASE, THE SERIES
ARE SAID TO BE COINTEGRATED. IF DIFFERENCING IS APPLIED TO A
COINTEGRATED PROCESS, THE MODEL WILL BE MISSPECIFIED. THE ISSUE OF
COINTEGRATION IS ADDRESSED IN THE NEXT SECTION, DEALING WITH GENERAL
MULTIVARIATE MODELS (SINCE IT IS UNLIKELY TO ARISE IN UNIVARIATE MODELS HAVING
EXOGENOUS REGRESSORS).
xt AND yt – βxt ARE STATIONARY,
FOR SOME VALUE OF β NOT EQUAL TO ONE IN MAGNITUDE.) IN THIS CASE, THE SERIES
ARE SAID TO BE COINTEGRATED. IF DIFFERENCING IS APPLIED TO A
COINTEGRATED PROCESS, THE MODEL WILL BE MISSPECIFIED. THE ISSUE OF
COINTEGRATION IS ADDRESSED IN THE NEXT SECTION, DEALING WITH GENERAL
MULTIVARIATE MODELS (SINCE IT IS UNLIKELY TO ARISE IN UNIVARIATE MODELS HAVING
EXOGENOUS REGRESSORS).
TESTS OF MODEL ADEQUACY
THE ADEQUACY OF THE MODEL REPRESENTATION IS TESTED BY TESTING WHETHER THE MODEL RESIDUALS ARE WHITE NOISE, AND WHETHER THE CROSS-CORRELATIONS OF THE PREWHITENED EXOGENOUS VARIABLE AND THE MODEL RESIDUALS IS ZERO.
A KEY ISSUE IN TESTING THE ADEQUACY OF TRANSFER FUNCTION MODELS IS THAT THE VARIANCES / COVARIANCES OF THE MODEL RESIDUALS DEPEND ON THE PARAMETERS OF THE MODEL. SEE BJRL FOR DETAILS.
MEASURES OF MODEL EFFICIENCY
THE EFFICIENCY OF THE MODEL REPRESENTATION IS ASSESSED BY MEANS OF THE AIC, BIC AND HQC CRITERIA (REDUNDANCY RECOGNIZED).
FORECASTING
FORECASTING WITH A TESTED TRANSFER-FUNCTION MODEL IS DONE IN A MANNER ANALOGOUS TO THAT DESCRIBED FOR UNIVARIATE MODELS CONTAINING NO EXOGENOUS VARIATES, BY DERIVING A RECURSIVE FORMULA FOR THE CURRENT VALUE OF yt FROM THE MODEL REPRESENTATION. SEE BJRL pp. 461-469 FOR DETAILS (FOR THE CASE IN WHICH THE MODEL ERROR TERM (FOR Yt) IS INDEPENDENT OF THE INPUT, Xt).
IN ORDER TO MAKE FORECASTS WITH A TRANSFER-FUNCTION MODEL, IT IS NECESSARY TO USE FORECASTS OF THE EXPLANATORY VARIABLE(S). (IF THE EXPLANATORY VARIABLE IS A STOCHASTIC PROCESS, THESE FORECASTS MIGHT BE DETERMINED, FOR EXAMPLE, FROM AN ARIMA MODEL OF THE EXPLANATORY VARIABLE(S).) THE AS DISCUSSED EARLIER, IN ORDER FOR THESE FORECASTS TO BE VALID, IT IS NECESSARY THAT STRONG EXOGENITY HOLD (THAT IS, THE OPTIMAL FORECASTS OF FUTURE VALUES OF Xt DEPEND ONLY ON PAST Xts, AND CANNOT BE IMPROVED BY KNOWLEDGE OF PAST Yts (SEE BJRL p. 463)).
PROCESS CONTROL; POLICY ANALYSIS
IF THE EXOGENOUS VARIABLE CAN BE CONTROLLED, THEN THE SYSTEM OUTPUT MAY BE CONTROLED BY SETTING ITS VALUE TO MINIMIZE THE MEAN SQUARED DIFFERENCE BETWEEN THE SYSTEM OUTPUT AND THE DESIRED (TARGET) OUTPUT. SEE BJRL pp. 559-615 FOR DETAILS.
AS DISCUSSED EARLIER, IN ORDER TO PREDICT THE EFFECT OF MAKING CHANGES IN THE EXPLANATORY VARIABLES, SUPER EXOGENEITY MUST HOLD.
TO USE A TRANSFER FUNCTION MODEL TO FORECAST A PROCESS THAT IS SIMPLY OBSERVED, NOT INTERFERED WITH, IT IS NECESSARY THAT THE MODEL BE DEVELOPED FROM DATA IN WHICH THE PROCESS IS SIMPLY OBSERVED, NOT INTERFERED WITH.
TO USE A TRANSFER FUNCTION MODEL TO CONTROL A PROCESS (AS IN POLICY ANALYSIS), IT IS NECESSARY THAT THE MODEL BE DEVELOPED FROM DATA IN WHICH FORCED CHANGES WERE MADE IN THE EXPLANATORY (CONTROL) VARIABLE. THIS ISSUE IS DISCUSSED ON PAGE 470 OF BJRL.
THE TOPIC OF PROCESS CONTROL IS DISCUSSED AT LENGTH IN BJRL. IN GENERAL, THE ATTEMPT IS TO ADJUST THE INPUT SO THAT THE OUTPUT COMES CLOSE TO A PARTICULAR VALUE, I.E., TO MINIMIZE THE MEAN-SQUARED-ERROR OF THE OUTPUT (RELATIVE TO A DESIRED TARGET VALUE). THERE ARE DIFFERENT TYPES OF PROCESS CONTROL, SUCH AS FEEDBACK CONTROL, FEEDFORWARD CONTROL, AND FEEDFORWARD-FEEDBACK CONTROL. SEE BJRL pp. 559-615 FOR A DETAILED DISCUSSION OF PROCESS CONTROL USING TRANSFER-FUNCTION MODELS.
FOR SIMPLE CONTROL SCHEMES, THE DESIRED SETTING FOR THE INPUT CAN BE DETERMINED BY ALGEBRA. IF IT IS DESIRED TO PLACE CONSTRAINTS ON THE INPUT, SUCH AS CONSTRAINTS ON ITS VARIANCE, THEN DIFFERENTIATION IS REQUIRED TO DETERMINE OPTIMAL INPUT. BJRL PRESENT A SIMPLE EXAMPLE OF THIS ON pp. 600 – 609. REINSEL (pp. 280 – 285) PRESENTS A GENERAL TREATMENT (“OPTIMAL FEEDBACK CONTROL IN ARMAX MODELS”). THE FIELD OF OPTIMAL CONTROL IS SUBSTANTIAL, INVOLVING MULTISTAGE TECHNIQUES SUCH AS DYNAMIC PROGRAMMING. IT IS MORE CONVENIENTLY REPRESENTED IN STATE-SPACE REPRESENATIONS OF PROCESSES. THESE TOPICS ARE NOT ADDRESSED IN THIS PRESENTATION. (EVEN FOR SIMPLE MODELS, SUCH THE INPUT THAT PRODUCES THE MINIMUM MEAN-SQUARED-ERROR OF THE OUTPUT, DIFFICULTIES MAY BE ENCOUNTERED. FOR EXAMPLE, THE OPTIMAL CONTROLLER MAY EXHIBIT OSCILLATORY “SAWTOOTH” BEHAVIOR. SUCH BEHAVIOR WOULD BE TOTALLY UNACCEPTABLE IN A POLITICAL APPLICATION INVOLVING THE SETTING OF INTEREST RATES, SINCE IT WOULD APPEAR THAT THE GOVERNMENT HAD NO IDEA WHAT IT WAS DOING.)
IMPULSE RESPONSE FUNCTION
THE IMPULSE RESPONSE FUNCTION AND STEP RESPONSE FUNCTIONS ARE ESTIMATED BY SUBSTITUTING THE ESTIMATED VALUES OF THE MODEL PARAMETERS IN THE FORMULA FOR THESE FUNCTIONS, AS FUNCTION OF THE MODEL PARAMETERS.
PREDICTION (FORECAST ERROR) VARIANCE DECOMPOSITION
IT IS OF INTEREST TO DECOMPOSE THE FORECAST ERROR VARIANCE INTO A PORTION ASSOCIATED WITH DEPENDENCE OF THE MODEL OUTPUT ON THE EXOGENOUS VARIABLE, AND THAT ASSOCIATED WITH THE MODEL ERROR TERM. THIS WILL BE DISCUSSED IN THE NEXT SECTION, DEALING WITH THE GENERAL MULTIVARIATE MODEL.
DETAILED EXAMPLE OF DEVELOPMENT AND APPLICATION OF A BIVARIATE TRANSFER-FUNCTION MODEL
A DETAILED DESCRIPTION OF THE PROCESS FOR IDENTIFYING, ESTIMATING AND APPLYING A BIVARIATE TRANSFER-FUNCTION MODEL IS PRESENTED IN BJRL (pp. 428 – 461 FOR FORECASTING AND pp. 559-615 FOR PROCESS CONTROL). THIS MATERIAL WILL NOT BE DISCUSSED IN THIS PRESENTATION.
4. GENERAL MULTIVARIATE TIME SERIES ANALYSIS
SIMILARITIES AND DIFFERENCES OF MULTIVARIATE TIME SERIES MODELS AND UNIVARIATE TIME SERIES MODELS (SINGLE VARIABLE AND MULTIPLE VARIABLE)
AS A POINT OF DEPARTURE FOR THIS SECTION ON GENERAL MULTIVARIATE TIME SERIES, WE SHALL START FROM THE UNIVARIATE TIME SERIES MODEL DISCUSSED IN THE PRECEDING SECTION.
REFERENCES ON UNIVARIATE TIME SERIES ANALYSIS WERE PROVIDED EARLIER. REFERENCES ON MULTIVARIATE TIME SERIES ANALYSIS INCLUDE:
BOX, GEORGE E. P., GWILYM M. JENKINS, GREGORY C. REINSEL AND GRETA M. LYUNG, TIME SERIES ANALYSIS, FORECASTING AND CONTROL, 5TH ED., WILEY, 2016. (THIS REFERENCE WILL BE DENOTED AS BJRL.)
LÜTKEPOHL, HELMUT, NEW INTRODUCTION TO MULTIPLE TIME SERIES ANALYSIS, SPRINGER, 2006
TSAY, RUEY S., MULTIVARIATE TIME SERIES ANALYSIS WITH R AND FINANCIAL APPLICATIONS, WILEY, 2014
TSAY, RUEY S., ANALYSIS OF FINANCIAL TIME SERIES, 3RD ED., WILEY, 2010
HAMILTON, JAMES D., TIME SERIES ANALYSIS, PRINCETON UNIVERSITY PRESS, 1994
REINSEL, GREGORY C., ELEMENTS OF MULTIVARIATE TIME SERIES ANALYSIS, 2ND ED., SPRINGER, 1997
LÜTKEPOHL, HELMUT AND MARKUS KRÄTZIG, APPLIED TIME SERIES ECONOMETRICS, CAMBRIDGE UNIVERSITY PRESS, 2004
ZIVOT, ERIC AND JIAHUI WANG, MODERN FINANCIAL TIME SERIES WITH S-PLUS 2ND ED., SPRINGER, 2006. POSTED AT INTERNET WEBSITE http://faculty.washington.edu/ezivot/econ589/manual.pdf .
AMISANO, GIANNI AND CARLO GIANNINI, TOPICS IN STRUCTURAL VAR ECONOMETRICS, 2ND ED., SPRINGER, 1997
DURBIN, J. AND S. J. KOOPMAN, TIME SERIES ANALYSIS BY STATE SPACE METHODS, 2ND ED., OXFORD UNIVERSITY PRESS, 2012
BANERJEE, ANINDYA, JUAN DOLADO, JOHN W. GALBRAITH AND DAVID F. HENDRY, CO-INTEGRATION, ERROR CORRECTION, AND THE ECONOMETRIC ANALYSIS OF NON-STATIONARY DATA, OXFORD UNIVERSITY PRESS, 1993
JOHANSEN, SØREN, LIKELIHOOD-BASED INFERENCE IN COINTEGRATED VECTOR AUTOREGRESSIVE MODELS, OXFORD UNIVERSITY PRESS, 1995
THE LEADING TEXT ON GENERAL CONTINUOUS NORMAL MULTIVARIATE STATISTICAL ANALYSIS (NOT FOCUSING ON TIME SERIES ANALYSIS) IS:
ANDERSON, T. W., AN INTRODUCTION TO MULTIVARIATE STATISTICAL ANALYSIS, 3RD ED., WILEY, 2003
THE DISCUSSION OF MULTIVARIATE TIME SERIES THAT IS PRESENTED IN BOX, JENKINS, REINSEL AND LJUNG (BJRL) IS COMPACT AND COMPREHENSIVE, AND WILL BE FOLLOWED IN THIS PRESENTATION. FOR MORE DETAILED DISCUSSION, SEE THE TEXTS BY LÜTKEPOHL, RUEY AND HAMILTON.
MULTIVARIATE TIME SERIES DESCRIPTORS
THE FUNDAMENTAL CONCEPTS OF MULTIVARIATE TIME SERIES, SUCH AS THE CONCEPT OF STATIONARITY AND THE DESCRIPTORS OF STATIONARY TIME SERIES, ARE ANALOGOUS TO THOSE FOR THE UNIVARIATE (SCALAR) CASE ALREADY DISCUSSED.
A RANDOM VECTOR Zt
= (Z1t,…,Zkt)’, t = 0, ![]() 1,
1, ![]() 2,… INDEXED ON TIME (t) IS A k-DIMENSIONAL TIME SERIES
VECTOR (OR VECTOR STOCHASTIC PROCESS, OR VECTOR PROCESS). EACH OF THE
COMPONENT RANDOM VARIABLE Zit OF Zt IS A
UNIVARIATE TIME SERIES.
2,… INDEXED ON TIME (t) IS A k-DIMENSIONAL TIME SERIES
VECTOR (OR VECTOR STOCHASTIC PROCESS, OR VECTOR PROCESS). EACH OF THE
COMPONENT RANDOM VARIABLE Zit OF Zt IS A
UNIVARIATE TIME SERIES.
THE VECTOR PROCESS Zt
IS STRICTLY STATIONARY IF THE PROBABILITY DISTRIBUTIONS OF THE RANDOM VECTORS (Zt1,
Zt2, …, Ztm) AND (Zt1+h, Zt2+h,
…, Ztm+h) ARE THE SAME FOR ANY SELECTION OF TIMES (t1,
t2,,…tm), ALL m, AND ALL LAGS OR LEADS h = 0, ![]() 1,
1, ![]() 2,….
2,….
FOR A STRICTLY STATIONARY PROCESS, THE MEAN (IF IT EXISTS) IS CONSTANT, E(Zt) = µ = (µ1, …, µk)’ AND THE COVARIANCE MATRIX (IF IT EXISTS) IS CONSTANT, E[(Zt - µ)(Zt - µ)’] = ΣZ.
THE k BY k MATRIX OF CROSS COVARIANCES AT LAG h (IF IT EXISTS) IS DEFINED AS
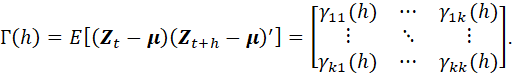
For h = 0, ![]() 1,
1, ![]() 2,…. THE CROSS-CORRELATIONS AT LAG h ARE DEFINED AS
2,…. THE CROSS-CORRELATIONS AT LAG h ARE DEFINED AS

WHERE
![]()
NOTE THAT ![]() =
= ![]() . FOR i = j
. FOR i = j ![]() DENOTES THE AUTOCORRELATION FUNCTION OF THE i-th
SERIES Zit, AND FOR i ≠ j
DENOTES THE AUTOCORRELATION FUNCTION OF THE i-th
SERIES Zit, AND FOR i ≠ j ![]() DENOTES THE CROSS-CORRELATION FUNCTION BETWEEN THE
SERIES Zit AND Zjt.
DENOTES THE CROSS-CORRELATION FUNCTION BETWEEN THE
SERIES Zit AND Zjt.
THE k BY k CROSS-CORRELATION MATRIX ρ(h) AT LAG h IS
![]()
FOR h = 0, ![]() 1,
1, ![]() 2,…, WHERE
2,…, WHERE
![]()
NOTE THAT Γ(h)’ = Γ(-h) AND ρ(h)’ = ρ(-h).
AS IN THE UNIVARIATE CASE, IT IS DIFFICULT TO ESTABLISH STRICT (STRONG) STATIONARITY, AND ATTENTION FOCUSES ON WEAK STATIONARITY, IN WHICH THE MEAN VECTOR AND COVARIANCE MATRIX DO NOT DEPEND ON t (ONLY ON h). WEAK STATIONARITY IS ALSO CALLED SECOND-ORDER STATIONARITY OR COVARIANCE STATIONARITY.
IN THE UNIVARIATE CASE, REPRESENTATIVE AUTOCORRELATION FUNCTIONS WERE DISPLAYED FOR VARIOUS CLASSES OF TIME SERIES (AUTOREGRESSIVE, MOVING AVERAGE, AUTOREGRESSIVE MOVING AVERAGE). BECAUSE OF THE SUBTANTIALLY INCREASED COMPLEXITY OF MULTIVARIATE TIME SERIES, CHARACTERIZATION OF TIME SERIES BY THE CROSS-CORRELATION FUNCTION IS SUBSTANTIALLY MORE DIFFICULT. THE EXAMINATION OF THE CROSS-CORRELATION FUNCTION SHOULD INVOLVE EXAMINATION OF THE AUTOCORRELATION FUNCTION OF EACH COMPONENT SERIES, JUST AS WAS DONE IN THE CASE OF UNIVARIATE TIME SERIES ANALYSIS. IT SHOULD ALSO INCLUDE EXAMINATION OF BIVARIATE CROSS-CORRELATION FUNCTIONS, AS DISCUSSED IN THE SECTION ON TRANSFER-FUNCTION MODELS.
AS IN THE UNIVARIATE CASE, WE SHALL DESCRIBE SOME MAJOR STATIONARY MULTIVARIATE TIME SERIES MODELS. THESE MODELS ARE ANALOGOUS TO THOSE DESCRIBED IN THE UNIVARIATE CASE, AND THEY WILL NOT BE DESCRIBED IN AS MUCH DETAIL. BEFORE PROCEEDING WITH THE DESCRIPTION OF GENERAL MODELS, WE WILL DESCRIBE A VERY BASIC ONE, THE VECTOR WHITE NOISE PROCESS, WHICH IS A BUILDING BLOCK IN THE CONSTRUCTION OF MORE COMPLEX MODELS.
IN THE UNIVARIATE CASE, WE INCLUDED SOME DISCUSSION OF THE POWER SPECTRUM AND THE SPECTRAL DENSITY FUNCTION. THESE SAME CONCEPTS APPLY TO THE CASE OF MULTIVARIATE TIME SERIES, BUT WE SHALL OMIT DISCUSSION OF THEM IN THIS PRESENTATION. SEE BJRL FOR DETAILS. AN ADVANTAGE OF THE SPECTRAL METHODS IS THAT THEY DO NOT REQUIRE PREWHITENING OF THE INPUT.
VECTOR WHITE NOISE PROCESS
A VECTOR WHITE NOISE PROCESS IS A SEQUENCE OF RANDOM VECTORS, …, a1,…,at,…, WHERE at = (a1t,…,akt)’, SUCH THAT E(at) = 0, E[ata’t] = Σ, AND E[ata’t+h] = 0 FOR h ≠ 0. THE COVARIANCE MATRICES ARE DENOTED AS:
![]()
THE WHITE NOISE PROCESS IS OF INTEREST PRIMARILY AS THE REPRESENTATION OF THE ERROR TERMS OF A MULTIVARIATE MODEL.
SINCE THE WHITE NOISE SEQUENCES OF THIS SECTION ARE ALMOST ALWAYS VECTOR WHITE NOISE SEQUENCES, WE SHALL GENERALLY DROP THE DESCRIPTOR “VECTOR” FROM THE TERM, AND GENERALLY REFER TO A VECTOR WHITE NOISE SEQUENCE SIMPLY AS A WHITE NOISE SEQUENCE.
WOLD’S REPRESENTATION OF A NONDETERMINISTIC STOCHASTIC PROCESS
THE MULTIVARIATE VERSION OF WOLD’S THEOREM ASSERTS THAT IF Zt IS A NONDETERMINISTIC STATIONARY PROCESS WITH MEAN VECTOR µ, THEN Zt CAN BE REPRESENTED AS AN INFINITE VECTOR MOVING AVERAGE (MA) PROCESS:
![]()
WHERE ![]() IS A k x k MATRIX IN THE BACKSHIFT OPERATOR B AND THE
k x k MATRICES Ψj SATISFY
IS A k x k MATRIX IN THE BACKSHIFT OPERATOR B AND THE
k x k MATRICES Ψj SATISFY ![]() AND at IS A VECTOR WHITE NOISE
PROCESS DEFINED ABOVE.
AND at IS A VECTOR WHITE NOISE
PROCESS DEFINED ABOVE.
THE COVARIANCE MATRIX OF Zt IS GIVEN BY
![]()
IN THE MOVING AVERAGE REPRESENTATION, THE COEFFICIENT MATRIX Ψi INDICATES THE RESPONSE OF THE OUTPUT VARIABLE Zt TO A UNIT CHANGE IN at-j, AND IS CALLED AN IMPULSE RESPONSE. IN THE CASE OF A UNIVARIATE MODEL, THE ats WERE UNCORRELATED, AND EACH IMPULSE RESPONSE COULD BE VIEWED INDEPENDENTLY OF THE OTHERS. IN THE MULTIVARIATE CASE, THE SITUATION IS DIFFERENT. THE INPUT at IS A VECTOR WHOSE COMPONENTS ARE CORRELATED. AS A RESULT, A CHANGE IN ONE COMPONENT OF THE ats IMPLIES A CHANGE IN THE OTHERS, AND IT IS NOT REASONABLE TO VIEW THE COEFFICIENT Ψj AS THE RESPONSE TO A UNIT CHANGE IN at. (SEE TSAY MTSA pp. 92-93 FOR DISCUSSION.)
IN ORDER FOR THE COEFFICIENTS OF THE MOVING AVERAGE REPRESENTATION TO BE EASILY INTERPRETED (AS IMPULSE RESPONSES), IT IS HELPFUL TO TRANSFORM THE MODEL TO ONE IN WHICH THE COMPONENTS OF THE VECTOR ERROR TERM ARE UNCORRELATED. THIS IS DONE BY MEANS OF A CHOLESKY TRANFORMATION.
SINCE Σ IS POSITIVE DEFINITE, IT MAY BE FACTORED AS Σ = LL’, WHERE L IS A LOWER TRIANGULAR MATRIX WITH POSITIVE DIAGONAL ELEMENTS. THE VARIABLE bt = L-1at HAS cov(bt) = Ik. THE MODEL MAY BE WRITTEN AS
![]()
WHERE ![]() AND
AND ![]() FOR j > 0. IN THIS REPRESENTATION, THE bj
ARE UNCORRELATED. IT IS MEANINGFUL TO CONSIDER THE OCCURRENCE OF A UNIT CHANGE
IN ONE COMPONENT OF bj INDEPENDENTLY OF THE OTHER COMPONENTS,
AND THE MATRIX
FOR j > 0. IN THIS REPRESENTATION, THE bj
ARE UNCORRELATED. IT IS MEANINGFUL TO CONSIDER THE OCCURRENCE OF A UNIT CHANGE
IN ONE COMPONENT OF bj INDEPENDENTLY OF THE OTHER COMPONENTS,
AND THE MATRIX ![]() IS READILY INTERPRETED (AS REFLECTING THE EFFECT OF A
UNIT CHANGE IN bt ON THE COMPONENTS OF Zt).
THE MATRICES
IS READILY INTERPRETED (AS REFLECTING THE EFFECT OF A
UNIT CHANGE IN bt ON THE COMPONENTS OF Zt).
THE MATRICES ![]() ARE CALLED THE IMPULSE RESPONSE WEIGHTS (OR IMPULSE
RESPONSE FUNCTION) WITH RESPECT TO THE ORTHOGONAL INNOVATIONS bj.
ARE CALLED THE IMPULSE RESPONSE WEIGHTS (OR IMPULSE
RESPONSE FUNCTION) WITH RESPECT TO THE ORTHOGONAL INNOVATIONS bj.
NOTE THAT THE CHOLESKY TRANSFORMATION DEPENDS ON THE ORDER OF THE COMPONENTS OF THE VECTOR at (OR Zt). IF THE COMPONENTS ARE REARRANGED, A DIFFERENT TRANSFORMATION RESULTS. THE USUAL PROCEDURE IS TO ARRANGE THE COMPONENTS IN AN ORDER THAT IS PHYSICALLY REASONABLE (IF SUCH AN ORDERING EXISTS), GIVEN THE NATURE OF THE APPLICATION.
NOTE ALSO THAT THIS PROCEDURE IS NOT WITHOUT ITS OWN DIFFICULTY. THE TRANSFORMED VARIABLES ARE LINEAR COMBINATIONS OF THE ORIGINAL VARIABLES, AND IT MAY BE DIFFICULT TO INTERPRET THE PHYSICAL MEANING OF THE TRANSFORMED VARIABLES. IN A SENSE, IN THIS APPROACH WE HAVE SUBSTITUTED ONE DIFFICULTY OR ANOTHER. IN ANY EVENT, IMPULSE RESPONSE ANALYSIS IS USUALLY DONE WITH RESPECT TO ORTHOGONALIZED VARIATES.
THEORETICAL STATIONARY MODELS: VECTOR MOVING AVERAGE PROCESS, VECTOR AUTOREGRESSIVE PROCESS, VECTOR AUTOREGRESSIVE MOVING AVERAGE PROCESS
THE BOX-JENKINS APPROACH TO MODELING TIME SERIES IS TO ASSUME THAT THE POLYNOMIAL Ψ(B) CAN BE APPROXIMATED BY THE PRODUCT Φ-1(B) Θ(B) WHERE Φ(B) AND Θ(B) ARE FINITE AUTOREGRESSIVE AND MOVING MATRIX POLYNOMIALS OF ORDERS p AND q, RESPECTIVELY. A VECTOR PROCESS INVOLVING ONLY A MOVING AVERAGE POLYNOMIAL IS CALLED A VECTOR MOVING AVERAGE (VMA) PROCESS; A VECTOR PROCESS INVOLVING ONLY AN AUTOREGRESSIVE POLYNOMIAL IS CALLED A VECTOR AUTOREGRESSIVE (VAR) PROCESS, AND A VECTOR PROCESS INVOLVING BOTH MOVING AVERAGE AND AUTOREGRESSIVE POLYNOMIALS IS CALLED A VECTOR AUTOREGRESSIVE MOVING AVERAGE (VARMA) PROCESS.
A PROCESS DEFINED AS ABOVE IS STATIONARY IF THE (VECTOR) ROOTS OF THE Φ POLYNOMIAL ARE OUTSIDE THE UNIT CIRCLE. IT IS INVERTIBLE (OR STABLE) IF THE ROOTS OF THE Θ POLYNOMIAL ARE OUTSIDE THE UNIT CIRCLE. INVERTIBILITY IS NECESSARY SO THAT THE CURRENT VALUE OF THE MODEL ERROR TERM CAN BE REPRESENTED AS A LINEAR COMBINATION OF PREVIOUS OBSERVATIONS, WITH WEIGHTS THAT TEND TO DIMINISH WITH INCREASING LAG, AND FOR WHICH THE SUM OF THE ABSOLUTE VALUES OF THE WEIGHTS IS BOUNDED. (ESTIMATION OF THE MODEL ERROR TERM IS IMPORTANT IN ESTIMATION OF PARAMETERS AND IN FORECASTING.)
FOR UNIVARIATE PROCESSES, THE MOVING-AVERAGE POLYNOMIAL ARISES IN MANY MODELS. THE PROCEDURE OF DIFFERENCING A SERIES TO ACHIEVE STATIONARITY (I.E., INTRODUCING THE AUTOREGRESSIVE POLYNOMIAL FACTOR (1 – B)) GENERALLY REQUIRES THAT A MOVING AVERAGE TERM OF THE FORM (1 – ΘB) BE PRESENENT THE MODEL. IF DIFFERENCING IS APPLIED WHEN IT IS NOT JUSTIFIED (I.E., THE DATA ARE “OVERDIFFERENCED”), THEN A FACTOR OF (1-B) IS INTRODUCED INTO THE MOVING AVERAGE POLYNOMIAL, CAUSING THE MODEL TO BE NONINVERTIBLE.
OVERDIFFERENCING IS MORE LIKELY TO OCCUR IN MULTIVARIATE TIME SERIES MODELS THAN IN UNIVARIATE TIME SERIES MODELS, FOR A REASON TO BE DISCUSSED LATER.
MOVING AVERAGE POLYNOMIALS ARE VERY IMPORTANT IN UNIVARIATE TIME SERIES MODELS, BUT TO SOME EXTENT LESS SO IN MULTIVARIATE TIME SERIES MODELS. THE REASON FOR THIS IS THAT THE INTRODUCTION OF COVARIATES INTO A MODEL GENERALLY DECREASES THE EXTENT OF AUTOCORRELATION OF THE MODEL RESIDUALS, THEREBY DIMINISHING THE IMPORTANCE OF THE MOVING-AVERAGE POLYNOMIAL. IN UNIVARIATE MODELS, COVARIATES TAKE THE FORM OF THE EXOGENOUS VARIABLES IN TRANSFER-FUNCTION MODELS. IN MULTIVARIATE MODELS, COVARIATES MAY BE EITHER OTHER COMPONENTS OF THE MULTIVARIATE OBSERVATION VECTOR, OR EXOGENOUS VARIABLES NOT INCLUDED IN THE OBSERVATION VECTOR.
BECAUSE OF THE PRECEDING FACT (THAT MOVING AVERAGE TERMS ARE LESS IMPORTANT IN VECTOR TIME SERIES MODELS THAN IN UNIVARIATE TIME SERIES MODELS), APPLIED TIME SERIES ANALYSIS INVOLVES VAR MODELS MUCH MORE THAN IT DOES VMA OR VARMA MODELS. FOR THAT REASON, IN THE DISCUSSION THAT FOLLOWS, WE DISCUSS VAR MODELS FIRST.
VECTOR AUTOREGRESSIVE (VAR) MODELS
A VECTOR AUTOREGRESSIVE MODEL OF ORDER p (DENOTED AS VAR(p)) IS DEFINED AS
![]()
OR
![]()
WHERE µ IS THE MEAN OF THE PROCESS,
![]()
Φi IS A k BY k PARAMETER MATRIX WITH Φp ≠ 0, AND at IS A VECTOR WHITE NOISE SEQUENCE WITH MEAN 0 AND COVARIANCE MATRIX Σ.
THE PROCESS IS STATIONARY IF ALL OF THE ROOTS OF THE DETERMINANTAL EQUATION det(Φ(B)) = 0 ARE GREATER THAN ONE IN ABSOLUTE VALUE, I.E., LIE OUTSIDE THE UNIT CIRCLE. WHEN THIS CONDITION IS SATISFIED, THE MODEL MAY BE WRITTEN AS AN INFINITE MOVING AVERAGE PROCESS,
![]()
OR
![]()
WHERE
![]()
AND THE COEFFICIENT
MATRICES SATISFY ![]() .
.
SINCE ![]() THE COEFFICIENT MATRICES MAY BE CALCULATED
RECURSIVELY FORM THE RELATION
THE COEFFICIENT MATRICES MAY BE CALCULATED
RECURSIVELY FORM THE RELATION
![]()
WHERE Ψ0 = I AND Ψj = 0 FOR j < 0.
REDUCED AND STRUCTURAL FORMS OF THE MODEL REPRESENTATION
IN THE CASE OF UNIVARIATE AUTOREGRESSIVE TIME SERIES MODELS, THE MODEL COULD BE REPRESENTED IN AUTOREGRESSIVE FORM OR IN MOVING AVERAGE FORM, AND THESE TWO REPRESENTATIONS WERE UNIQUE. IN THE CASE OF MULTIVARIATE AUTOREGRESSIVE TIME SERIES MODELS, A VARIETY OF REPRESENTATIONS IS AVAILABLE. TWO STANDARD REPRESENTATIONS ARE THE STRUCTURAL FORM AND THE REDUCED FORM.
THE REDUCED FORM IS THE WOLD DECOMPOSITION, OR MOVING AVERAGE REPRESENTATION, JUST DESCRIBED ABOVE. THE VAR MODEL IS:
![]()
WHERE ![]() ,
, ![]() IS A k x k PARAMETER MATRIX, AND at
IS A VECTOR WHITE NOISE SEQUENCE WITH MEAN 0 AND COVARIANCE MATRIX Σ. FOR
A VAR PROCESS, THE MOVING AVERAGE REPRESENTATION IS A UNIQUE REPRESENTATION OF
THE STOCHASTIC PROCESS (AMONG MOVING AVERAGE REPRESENTATIONS).
IS A k x k PARAMETER MATRIX, AND at
IS A VECTOR WHITE NOISE SEQUENCE WITH MEAN 0 AND COVARIANCE MATRIX Σ. FOR
A VAR PROCESS, THE MOVING AVERAGE REPRESENTATION IS A UNIQUE REPRESENTATION OF
THE STOCHASTIC PROCESS (AMONG MOVING AVERAGE REPRESENTATIONS).
FOR THE STRUCTURAL FORM, WE TRANSFORM THE MODEL TO ONE IN WHICH THE MODEL RESIDUALS ARE UNCORRELATED (BUT NOT OF UNIT VARIANCES, AS WAS DONE FOR THE ORTHOGONAL-INNOVATIONS TRANSFORMATION DONE FOR THE IMPULE RESPONSE FUNCTION).
SINCE Σ IS POSITIVE
DEFINITE, THERE EXISTS A LOWER TRIANGULAR MATRIX ![]() WITH ONES ON THE DIAGONAL SUCH THAT
WITH ONES ON THE DIAGONAL SUCH THAT ![]() IS A DIAGONAL MATRIX WITH POSITIVE DIAGONAL
ELEMENTS. PREMULTIPLYING THE VAR MOLDEL BY
IS A DIAGONAL MATRIX WITH POSITIVE DIAGONAL
ELEMENTS. PREMULTIPLYING THE VAR MOLDEL BY ![]() PRODUCES THE MODEL
PRODUCES THE MODEL
![]()
WHERE ![]() AND
AND ![]() , AND cov(
, AND cov(![]() ) =
) = ![]() .
.
THIS MODEL SHOWS THE
CONCURRENT RELATIONSHIP AMONG THE COMPONENTS OF Zt. IT IS
CALLED A STRUCTURAL FORM OR STRUCTURAL REPRESENTATION OF THE MODEL. SINCE ![]() IS LOWER TRIANGULAR, EACH OF THE COMPONENTS OF Zt
IS DEFINED, IN ORDER, AS A FUNCTION OF PREVIOUSLY DEFINED COMPONENTS. IT IS
HENCE A RECURSIVE SPECIFICATION, WHICH DEPENDS ON THE ORDERING OF THE
COMPONENTS. WHAT ORDERING IS SELECTED DEPENDS ON THE NATURE OF THE
APPLICATION.
IS LOWER TRIANGULAR, EACH OF THE COMPONENTS OF Zt
IS DEFINED, IN ORDER, AS A FUNCTION OF PREVIOUSLY DEFINED COMPONENTS. IT IS
HENCE A RECURSIVE SPECIFICATION, WHICH DEPENDS ON THE ORDERING OF THE
COMPONENTS. WHAT ORDERING IS SELECTED DEPENDS ON THE NATURE OF THE
APPLICATION.
FOR A SPECIFIED ORDERING, THE STRUCTURAL SPECIFICATION UNIQUELY DEFINES THE STOCHASTIC PROCESS. (THAT IS, THE MODEL IS IDENTIFIED, OR IDENTIFIABLE, OR ESTIMABLE.) ALTHOUGH MODEL UNIQUENESS IS NOT ESSENTIAL TO SOME APPLICATIONS (E.G., FORECASTING) UNIQUENESS IS CRUCIAL TO ESTIMATION; IF A PROCESS CAN BE REPRESENTED BY MULTIPLE MODEL SPECIFICATIONS, THEN THE NUMERICAL PROCEDURES USED TO ESTIMATE MODEL PARAMETERS MAY NEVER CONVERGE TO A SOLUTION.
RELATIONSHIP TO TRANSFER FUNCTION MODEL
THE TRANSFER FUNCTION MODEL DISCUSSED EARLIER IS A SPECIAL CASE OF THE VECTOR AUTOREGRESSIVE MODEL IN WHICH THE OUTPUT VARIABLES DEPEND ON PAST VALUES OF THE INPUT VARIABLES, BUT THE INPUT VARIABLES DO NOT DEPEND ON PAST VALUES OF THE OUTPUT VARIABLE (“STRONG EXOGENEITY”). IN ADDITION, THE ERROR TERMS FOR THE OUTPUT VARIABLES MUST NOT BE CORRELATED WITH THE INPUT VARIABLES. SATISFYING THIS REQUIREMENT MAY REQUIRE A TRANSFORMATION OF VARIABLES. SEE BJRL p. 512 FOR DISCUSSION.
VECTOR MOVING AVERAGE (VMA) MODEL
A VECTOR MOVING AVERAGE PROCESS OF ORDER q (DENOTED AS MA(q)) IS DEFINED AS
![]()
OR
![]()
WHERE µ IS THE MEAN OF THE PROCESS,
![]()
Θi IS A k BY k PARAMETER MATRIX WITH Θq ≠ 0, AND at IS A VECTOR WHITE NOISE SEQUENCE WITH MEAN 0 AND COVARIANCE MATRIX Σ.
JUST AS IN THE UNIVARIATE CASE, A VECTOR MOVING AVERAGE MODEL MAY BE PREFERRED TO A VECTOR AUTOREGRESSIVE MODEL, IN A SITUATION WHERE A VMA MODEL OF LOW ORDER q MAY PROVIDE AN ADEQUATE REPRESENTATION, BUT AN AUTOREGRESSIVE MODEL WOULD REQUIRE A HIGH ORDER p.
IN PRACTICAL APPLICATIONS, A PURE VMA IS UNUSUAL. MOST REAL-WORLD APPLICATIONS ARE BETTER REPRESENTED BY VARs OR VARMAs. HISTORICALLY, ECONOMETRICIANS MIGHT FIT AN AUTOREGRESSIVE (LAGGED-VARIABLE) MODEL TO DATA, AND THEN USE A PURE MOVING AVERAGE MODEL TO REPRESENT THE AUTOCORRELATION STRUCTURE OF THE MODEL RESIDUALS.
A VECTOR MOVING AVERAGE PROCESS IS UNIQUE (I.E., NO TWO SUCH PROCESSES HAVING DIFFERENT PARAMETER VALUES REPRESENT THE SAME STOCHASTIC PROCESS). THAT IS, THE PARAMETERS ARE ESTIMABLE.
VECTOR AUTOREGRESSIVE MOVING AVERAGE (VARMA) PROCESS
IF THE MOVING AVERAGE REPRESENTATION OF THE WOLD DECOMPOSITION CAN BE APPROXIMATELY REPRESENTED BY A POLYNOMIAL PRODUCT OF THE FORM
![]()
WHERE Φ(B) AND Θ(B) ARE THE AUTOREGRESSIVE AND MOVING AVERAGE POLYNOMIALS DEFINED EARLIER, THEN THE MODEL IS A VECTOR AUTOREGRESSIVE – MOVING AVERAGE MODEL (DENOTED BY VARMA(p,q)):
![]()
WHERE ![]() IS AVECTOR WHITE NOISE SEQUENCE WITH MEAN 0
AND COVARIANCE MATRIX Σ.
IS AVECTOR WHITE NOISE SEQUENCE WITH MEAN 0
AND COVARIANCE MATRIX Σ.
THE VARMA MODEL MAY BE REPRESENTED IN REDUCED (MOVING AVERAGE) OR STRUCTURAL FORMS, IN THE SAME WAY AS THE VAR MODEL. IN THE CASE OF THE VAR, THE STRUCTURAL REPRESENTATION WAS UNIQUE. IN THE CASE OF THE VARMA, THIS IS NO LONGER TRUE.
IN THE UNIVARIATE CASE, AN ARMA REPRESENTATION IS UNIQUE, AS LONG AS IDENTICAL FACTORS DO NOT OCCUR IN THE AR AND MA POLYNOMIALS. IN THE MULTIVARIATE CASE, A MORE COMPLICATED CONDITION MUST BE IMPOSED TO OBTAIN UNIQUENESS OF THE MODEL REPRESENTATION. UNIQUENESS IS DESIRED SO THAT THE MODEL IS ESTIMABLE (IDENTIFIED, IDENTIFIABLE). IT IS NOT REQUIRED FOR SOME FORECASTING APPLICATIONS, BUT IS FOR OTHERS.
THE CONDITIONS REQUIRED TO ASSURE UNIQUENESS ARE A LITTLE COMPLICATED, AND ARE DISCUSSED (FOR EXAMPLE) ON pp. 528-529 OF BJRL. THESE CONDITIONS ARE SUMMARIZED IN THE NEXT SECTION.
THE VECTOR AUTOREGRESSIVE MOVING AVERAGE MODEL DOES NOT ARISE IN PRACTICE NEARLY AS OFTEN AS THE VECTOR AUTOREGRESSIVE MODEL. ONCE COVARIATES ARE INTRODUCED INTO A MODEL (AS THE COMPONENTS OF THE MULTIVARIATE OBSERVATION VECTOR), AUTOREGRESSIVE TERMS ARE GENERALLY REQUIRED TO OBTAIN AN ADEQUATE REPRESENTATION; AND, ONCE THEY ARE INCLUDED, THE NEED FOR MOVING AVERAGE TERMS IS REDUCED (AS DISCUSSED EARLIER). ON THE OTHER HAND, ONCE DIFFERENCING IS APPLIED TO ACHIEVE STATIONARITY, INCORPORATION OF A SIMILAR FACTOR (WITH ROOT OUTSIDE THE UNIT CIRCLE) IS OFTEN NECESSITATED. THAT IS, THE REQUIREMENT FOR ADDING A MOVING AVERAGE COMPONENT TO A VAR MODEL IS OFTEN A TECHNICAL ISSUE, NOT A SUBSTANTIVE ONE. AS WILL BE DISCUSSED IN THE FOLLOWING SECTION, ESTIMATION OF VARMA MODELS IS DIFFICULT, AND THAT FACT ALONE ACCOUNTS FOR LESSENED USE OF THAT MODEL CLASS IN APPLICATIONS.
PROBLEMS ASSOCIATED WITH VARMA MODELS: EXCHANGEABILITY, OBSERVATIONAL EQUIVALENCE, IDENTIFIABILITY
EXCHANGEABILITY (OBSERVATIONAL EQUIVALENCE)
TWO DIFFERENT ARMA MODELS (I.E., TWO ARMA MODELS OF DIFFERENT ORDERS (VALUES OF p AND q)) ARE SAID TO BE EXCHANGEABLE IF THEY CORRESPOND TO THE SAME COVARIANCE STRUCTURE OF A PROCESS, OR, EQUIVALENTLY, HAVE THE SAME WOLD REPRESENTATION (INFINITE MOVING AVERAGE REPRESENTATION). TWO EXCHANGEABLE ARMA MODELS ARE SAID TO BE OBSERVATIONALLY EQUIVALENT. SEE REINSEL pp. 40-41 FOR DETAILS.
THE OCCURRENCE OF EXCHANGEABLE MODELS CAN BE CAUSED BY THE PRESENCE OF A UNIMODULAR MATRIX FACTOR IN AN AR OR MA MATRIX POLYNOMIAL. A MATRIX IS UNIMODULAR IF AND ONLY IF ITS INVERSE EXISTS AND IS A MATRIX POLYNOMIAL OF FINITE DEGREE, OR (EQUIVALENTLY) IF AND ONLY IF ITS DETERMINANT IS A NONZERO CONSTANT.
FOR EXAMPLE, SUPPOSE THAT U(B) IS A UNIMODULAR MATRIX OPERATOR POLYNOMIAL. THEN THE PROCESS Zt = U(B)Θ(B)at IS EQUIVALENT TO THE PROCESS U(B)-1 Zt = Θ(B)at.
AS AN EXAMPLE OF EXCHANGEABLE MODELS, CONSIDER THE BIVARIATE MA(1) MODEL Zt = at – Θat-1 AND THE BIVARIATE AR(1) MODEL Zt – ΦZt-1 = at, WHERE
![]()
AND
![]()
THESE MODELS ARE EXCHANGEABLE SINCE (1 – ΘB)-1 = (1 + ΘB).
NOTE THAT ALTHOUGH THESE MODELS ARE EXCHANGEABLE, THEY ARE NEVERTHELSS IDENTIFIABLE. THAT IS, THE MA(1) SPECIFICATION IS UNIQUE AMONG ALL MA(1) MODELS, AND THE AR(1) SPECIFICATION IS UNIQUE AMONG ALL AR(1) MODELS. WITHIN THE MODEL CLASS, THE MODEL IS UNIQUE, AND THE PARAMETER MAY BE ESTIMATED WITHOUT ANY PROBLEM.
IN ANY EVENT, THE PRESENCE OF EXCHANGEABILITY MAY CAUSE A PROBLEM IN INTERPRETATION AND UNDERSTANDING OF AN APPLICATION, SINCE THE MODELS ARE COMPLETELY DIFFERENT YET CORRESPOND TO THE SAME PROCESS (AND COVARIANCE FUNCTION).
IDENTIFIABILITY
EVEN MORE SERIOUS THAN THE PHENOMENON OF EXCHANGEABILITY IS THE ISSUE OF IDENTIFIABILITY. A VARMA MODEL MAY BE MULTIPLIED ON BOTH SIDES BY A UNIMODULAR MATRIX TO FORM AN OBSERVATIONALLY EQUIVALENT MODEL OF DIFFERENT ORDER. SEE BJRL, REINSEL OR LÜTKEPOHL FOR DISCUSSION.
FOR EXAMPLE, CONSIDER THE BIVARIATE VARMA(1,1) MODEL OBTAINED BY MULTIPLYING BOTH SIDES OF THE ABOVE MA(1) MODEL Zt = at – Θat-1 BY THE UNIMODULAR FACTOR U(B) = I - Φ*B. THIS MODEL IS Zt – Φ*Zt-1 = at – Θ*at-1, WHERE
![]()
AND
![]()
THIS MODEL IS OBSERVATIONALLY EQUIVALENT TO BOTH THE AR(1) AND MA(1) MODELS DEFINED ABOVE, FOR ANY VALUE OF α. FOR EXAMPLE,
![]()
AS A RESULT, SINCE α IS ARBITRARY, THE PARAMETERS Φ* AND Θ* IN THE VARMA(1,1) MODEL ARE NOT IDENTIFIABLE.
THIS SITUATION IS ANALOGOUS TO THE SITUATION IN UNIVARIATE ARMA MODELS, WHERE THE PRESENCE OF COMMON FACTORS IN THE AR AND MA POLYNOMIALS CAUSES PROBLEMS. IN THE MULTIVARIATE CASE, IT DOES NOT SUFFICE SIMPLY TO REMOVE COMMON FACTORS. IN ORDER FOR A VARMA TO BE IDENTIFIABLE, THE FOLLOWING CONDITIONS MUST HOLD FOR THE AR MATRIX Φ(B) AND THE MA MATRIX Θ(B):
1. THE MATRICES Φ(B) AND Θ(B) HAVE NO COMMON LEFT FACTORS OTHER THAN UNIMODULAR ONES (I.E., THEY ARE LEFT-COPRIME).
2. WITH q AS SMALL AS POSSIBLE AND p AS SMALL AS POSSIBLE FOR THAT q, THE JOINT MATRIX [Φp, Θq] MUST BE OF RANK k, THE DIMENSION OF Zt.
IT IS EMPHASIZED THAT SIMPLY REMOVING COMMON FACTORS, EVEN IF THEY ARE UNIMODULAR, DOES NOT SUFFICE TO ACHIEVE UNIQUENESS IN A MULTIVARIATE VARMA REPRESENTATION. THE SECOND CONDITION IS ESSENTIAL.
BECAUSE OF THE POSSIBILITY OF LACK OF UNIQUENESS AND THE COMPLEXITY OF THE METHOD FOR OVERCOMING IT, THE PROCESS OF ESTIMATING PARAMETERS FOR VARMA MODELS IS COMPLICATED. VAR AND MA MODELS DO NOT SUFFER FROM THIS LACK-OF-UNIQUENESS PROBLEM. THIS SITUATION IS A SIGNIFICANT REASON WHY THE USE OF VAR MODELS IS MUCH MORE WIDESPREAD THAN THE USE OF VARMA MODELS, DESPITE THE FACT THAT THE LATTER MAY BE MORE EFFICIENT REPRESENTATIONS (I.E., INVOLVE FEWER PARAMETERS, OR MEASURE BETTER WITH RESPECT TO MODEL PERFORMANCE MEASURES SUCH AS THE AIC, BIC AND HQC).
EXOGENOUS VARIABLES
COVARIATES ARE VARIABLES (RANDOM OR OTHERWISE) RELATED TO THE RESPONSE VARIABLE OF INTEREST. COVARIATES MAY BE EITHER COMPONENTS OF THE MULTIVARIATE OBSERVATION VECTOR (I.E., OF A JOINT DISTRIBUTION) OR EXOGENOUS VARIABLES. EXOGENOUS VARIABLES WERE DISCUSSED EARLIER, IN THE SECTION ON TRANSFER-FUNCTION MODELS. EXOGENOUS VARIABLES MAY BE INCLUDED AS COMPONENTS OF A MULTIVARIATE RESPONSE VARIABLE, BUT THAT IS NOT AS REASONABLE A REPRESENTATION AS INCLUDING THEM AS SEPARATE EXPLANATORY VARIABLES.
MULTIVARIATE MODELS THAT INCLUDE EXOGENOUS VARIABLES ARE REFERRED TO AS VARX AND VARMAX MODELS.
NONSTATIONARITY AND COINTEGRATION
MANY REAL-WORLD TIME SERIES EXHIBIT NONSTATIONARY BEHAVIOR. FOR UNIVARITE TIME SERIES ANALYSIS, THE STANDARD APPROACH TO REPRESENTING HOMOGENEOUS NONSTATIONARY BEHAVIOR IS TO ALLOW THE AUTOREGRESSIVE POLYNOMIAL TO INCLUDE ONE OR MORE ROOTS ON THE UNIT CIRCLE. ONE WAY OF INCLUDING UNIT ROOTS IN A MODEL IS THROUGH DIFFERENCING THE DATA. IN APPLYING DIFFERENCING, IT IS IMPORTANT TO NOT DIFFERENCE A SERIES PAST THE POINT AT WHICH STATIONARITY IS ACHIEVED, OR ELSE A UNIT ROOT WILL BE INSERTED INTO THE MOVING AVERAGE POLYNOMIAL, AND THE SERIES WILL BE NONINVERTIBLE.
WITH A MULTIVARIATE TIME SERIES, THE APPROACH OF DIFFERENCING THE DATA MUST BE APPROACHED WITH CAUTION. THE APPROACH OF APPLYING DIFFERENCING TO ALL SERIES TO RENDER THEM STATIONARY IS PROBLEMATIC. THIS APPROACH OBVIOUSLY DOES NOT WORK IF SOME OF THE COMPONENTS ARE STATIONARY, SINCE IT WOULD LEAD TO OVERDIFFERENCING OF THOSE COMPONENTS.
AN APPROACH THAT WORKS IN SOME SITUATIONS IS TO DIFFERENCE EACH COMPONENT SERIES SEPARATELY, THE NUMBER OF TIMES REQUIRED TO ACHIEVE STATIONARITY. IF THIS IS DONE, THE MODEL IS OF THE FORM:
![]()
WHERE
![]()
IS A DIAGONAL MATRIX, d1,…,dk ARE NONNEGATIVE INTEGERS, AND det[Φ1(B)] = 0 HAS ALL ROOTS GREATER THAN ONE IN ABSOLUTE VALUE. THE TRANSFORMED VECTOR SERIES
![]()
IS A STATIONARY VARMA(p,q) PROCESS.
IN THE PRECEDING METHOD, THE REUQIUREMENT THAT det[Φ1(B)] = 0 HAS ALL ROOTS GREATER THAN ONE IN ABSOLUTE VALUE IS ESSENTIAL. IT IS NOT SATISFIED IF THERE EXIST LINEAR COMBINATIONS OF THE DATA SUCH THAT THE NUMBER OF DIFFERENCES REQUIRED TO ACHIEVE STATIONARITY FOR THE LINEAR COMBINATONS IS LOWER THAN THE NUMBER OF DIFFERENCES REQUIRED TO ACHIEVE STATIONARITY OF EACH COMPONENT SERIES. IF THIS SITUATON APPLIES, THEN THE TRANSFORMED SERIES WILL NOT BE INVERTIBLE, AND PROBLEMS WILL ARISE IN ESTIMATION AND FORECASTING.
FOR EXAMPLE, SUPPOSE THAT EVERY COMPONENT SERIES Zit IS NONSTATIONARY, THAT THE FIRST DIFFERENCES (1 – B)Zit ARE STATIONARY, BUT THAT CERTAIN LINEAR COMBINATIONS Yit = bi’Zt ARE STATIONARY. IN THIS CASE, THE COMPONENT TIME SERIES ARE SAID TO BE COINTEGRATED WITH COINTEGRATING VECTORS bi. IF DIFFERENCING IS APPLIED TO ALL TIME SERIES IN THIS CASE, OVERDIFFERENCING WILL RESULT (EVEN THOUGH ALL SERIES ARE INDIVIDUALLY NONSTATIONARY)), AND PROBLEMS WILL ARISE (IN ESTIMATION AND FORECASTING).
A TIME SERIES Zt IS SAID TO BE AN INTEGRATED PROCESS OF ORDER d (DENOTED AS I(d)), IF (1 – B)dZt IS STATIONARY AND INVERTIBLE, WHERE d > 0. THE NUMBER d IS CALLED THE ORDER OF INTEGRATION, AND IT INDICATES THE MULTIPLICITY OF THE UNIT ROOT. IF Zit ARE I(d) NONSTATIONARY AND b’Zt IS I(h) WITH h < d, THEN Zt IS COINTEGRATED. THE VECTOR b IS CALLED A COINTEGRATING VECTOR. IN PRACTICAL APPLICATIONS, THE MAJOR CASE IS d = 1 AND h = 0.
THE PRECEDING DEFINITION REFERS TO A SINGLE COINTEGRATING VECTOR. IN GENERAL, THERE MAY BE MORE THAN ONE LINEARLY INDEPENDENT COINTEGRATING VECTOR. CONSIDER A NONSTATIONARY VARMA MODEL Φ(B)Zt = Θ(B)at HAVING d < k ROOTS EQUAL TO ONE AND OTHER ROOTS GREATER THAN ONE IN ABSOLUTE VALUE. THEN THE MATRIX Φ(1) = I – Φ1 - … - Φp HAS RANK r = k – d, AND IT CAN BE ESTABLISHED THAT r LINEARLY INDEPENDENT VECTORS bi EXIST SUCH THAT bi’Zt IS STATIONARY. IN THIS CASE, Zt IS SAID TO HAVE COINTEGRATING RANK r.
COINTEGRATION IS EXHIBITED BY SERIES HAVING A COMMON TREND, SUCH AS THE VALUE OF CURRENCY IN DIFFERENT MARKETS, OR OTHER CLOSELY RELATED ECONOMIC SERIES.
THE ERROR CORRECTION MODEL
A STANDARD MODEL USED TO REPRESENT COINTEGRATION IS THE ERROR CORRECTION (EC) MODEL. AS ABOVE, LET US ASSUME A MODEL OF THE FORM Φ(B)Zt = Θ(B)at WHERE det[Φ(B)] = 0 HAS d < k ROOTS EQUAL TO ONE AND ALL OTHER ROOTS GREATER THAN ONE IN ABSOLUTE VALUE. A PROCESS DESCRIBED BY THIS MODEL IS CALLED PARTIALLY NONSTATIONARY. THIS MODEL IS SAID TO BE REPRESENTED IN ERROR-CORRECTION FORM IF IT IS EXPRESSED AS FOLLOWS:
![]()
WHERE
![]()
![]()
AND
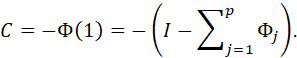
THIS MODEL DIFFERS FROM ONE INVOLVING TRANSFORMATION TO A DIFFERENCED VARIATE (1-B)Zt IN THAT THE DIFFERENCE OCCURS ON THE LEFT-HAND-SIDE OF THE MODEL BUT THE UNDIFFERENCED VARIATE Zt (THE “LEVEL” OF THE VARIATE) OCCURS ON THE RIGHT-HAND SIDE. THE MOTIVATION FOR THE MODEL IS THAT THE VARIATE Zt TENDS TO MOVE TO THE RECENT LEVEL OF THE SERIES (IN CONTRAST TO A FIRST-DIFFERENCE MODEL IN WHICH THE VARIATE Zt TENDS TO MOVE TO THE PRECEDING VALUE OF THE VARIATE). THAT IS, THE PROCESS TENDS TO “CORRECT” DEPARTURES FROM THE RECENT MEAN.
METHODS OF MODEL SIMPLIFICATION: ASSUMPTIONS, RESTRICTIONS, CANONICAL CORRELATION ANALYSIS, PRINCIPAL COMPONENTS ANALYSIS
A MAJOR DIFFICULTY ASSOCIATED WITH MULTIVARIATE TIME SERIES MODELS IS THAT THE VERY LARGE NUMBER OF PARAMETERS MAKES IT DIFFICULT TO DETERMINE A REASONABLE MODEL. A NUMBER OF APPROACHES ARE AVAILABLE TO ASSIST THE MODEL IDENTIFICATION PROCESS. THESE INCLUDE:
1. MODEL SPECIFICATION GUIDED BY SUBSTANTIVE THEORY (E.G., BY ECONOMIC THEORY, IN AN ECONOMIC APPLICATION). FOR THIS APPROACH, IT IS OFTEN EASIER TO WORK WITH THE STRUCTURAL FORM OF THE MODEL (INSTEAD OF THE REDUCED FORM).
2. REDUCTION IN THE NUMBER OF VARIABLES, BY DISCARDING VARIABLES THAT ARE HIGHLY CORRELATED WITH OTHERS.
3. REDUCTION IN THE NUMBER OF VARIABLES BY REPLACING SETS OF VARIABLES WITH LINEAR COMBINATIONS THAT ACCOUNT FOR MUCH OF THE VARIATION IN THE ORIGINAL VARIABLES.
TO ASSIST REDUCTION IN THE NUMBER OF VARIABLES, STANDARD MULTIVARIATE ANALYSIS TOOLS, SUCH AS CANONICAL CORRELATION AND PRINCIPAL COMPONENTS ANALYSIS ARE AVAILABLE.
AFTER THE VARIABLE SET HAS BEEN REDUCED AS MUCH AS POSSIBLE, THE VARIOUS TIME SERIES DESCRIPTORS, SUCH AS THE CROSS-CORRELATION FUNCTION, MAY BE EXAMINED TO SUGGEST REASONABLE ORDERS FOR TENTATIVE MODELS. INITIALLY, ATTENTION SHOULD FOCUS ON THE USE OF VAR REPRESENTATIONS, SINCE THE IDENTIFICATION AND ESTIMATION PROCEDURES FOR THIS CLASS OF MODELS IS SIMPLER THAN FOR ARMA MODELS.
THE IDENTIFICATION PROCESS FOR MULTIVARIATE MODELS IS SIMILAR TO THAT FOR UNIVARIATE MODELS (ESPECIALLY TRANSFER-FUNCTION MODELS) AND WILL NOT BE DESCRIBED IN FURTHER DETAIL HERE. SEE BJRL, TSAY MTSA, LÜTKEPOHL OR HAMILTON FOR DETAILS.
STATIONARITY TRANSFORMATIONS AND TESTS (FOR HOMOGENEITY, COINTEGRATION)
THE VAR, VMA AND VARMA MODELS ARE USED TO REPRESENT STATIONARY TIME SERIES. IF THE OBSERVED DATA ARE NONSTATIONARY, IT IS NECESSARY TO TRANSFORM THE DATA TO STATIONARY VARIABLES OR IDENTIFY A COINTEGRATED REPRESENTATION.
NONSTATIONARY BEHAVIOR OF COMPONENT SERIES IS ASSESSED IN THE SAME FASHION AS WAS USED FOR UNIVARIATE PROCESSES. COINTEGRATED BEHAVIOR IS ASSESSED BY OBSERVING THAT COMPONENTS THAT ARE NONSTATIONARY MOVE TOGETHER.
TESTS FOR UNIT ROOTS WERE DESCRIBED EARLIER.
AIDS TO MODEL IDENTIFICATION
IN ADDITION TO THE PROCEDURES THAT ARE ANALOGOUS TO THOSE USED FOR SINGLE-VARIABLE UNIVARIATE OR TRANSFER-FUNCTION MODELS (I.E., THE ACF, PACF AND CCF), A NUMBER OF OTHER PROCEDURES ARE AVAILABLE TO ASSIST MODEL IDENTIFICATION IN THE MULTIVARIATE CASE, FOR VARMA MODELS. THESE INCLUDE THE USE OF KRONECKER INDICES, SCALAR COMPONENT MODELS, AND ORDER DETERMINATION USING LINEAR LEAST SQUARES.
GRANGER-CAUSALITY TESTS
IN FORECASTING A MULTIVARIATE MODEL, TWO CASES ARISE. THE FIRST IS THE PROBLEM OF MAKING UNCONDITIONAL FORECASTS, AND THE SECOND IS THE PROBLEM OF MAKING FORECASTS CONDITIONAL ON SPECIFIED VALUES FOR SOME OF THE COMPONENT VARIABLES OR EXOGENOUS VARIABLES. IN ORDER TO DO CONDITONAL FORECASTING, IT IS NECESSARY TO IDENTIFY THE EXOGENEITY PROPERTIES OF THE EXPLANATORY VARIABLES. THIS TOPIC WAS DISCUSSED IN THE SECTION ON TRANSFER-FUNCTION MODELS.
THE ISSUE OF MAKING CONDITIONAL FORECASTS AND ASSESSING VARIABLE EXOGENEITY FALLS IN THE REALM OF CAUSAL MODELING AND ANALYSIS. CAUSAL MODELING IS BEST GUIDED BY SUBSTANTIVE KNOWLEDGE, BUT IN SOME CASES IT CAN BE ASSISTED BY STATISTICAL ANALYSIS. IN THIS RESPECT, A RELEVANT TOPIC IS THE NOTION OF GRANGER CAUSALITY.
WITHIN A MODEL, A VARIABLE IS SAID TO BE A GRANGER CAUSE OF ANOTHER IF INFORMATION ABOUT THE FIRST VARIABLE REDUCES THE FORECAST ERROR VARIANCE OF THE SECOND, CONDITIONAL ON ALL OTHER VARIABLES IN THE MODEL. TWO VARIABLES MAY BE GRANGER CAUSES OF EACH OTHER, IN WHICH CASE THE VARIABLES ARE SAID TO HAVE INSTANTANEOUS GRANGER CAUSALITY.
ESTIMATION
THE PARAMETERS OF AN IDENTIFIED MULTIVARIATE TIME SERIES MODEL ARE ESTIMATED USING THE SAME TECHNIQUES AS WERE DESCRIBED EARLIER FOR UNIVARIATE TIME SERIES MODELS. THESE INCLUDE THE METHOD OF MOMENTS, THE METHOD OF LEAST SQUARES, THE METHOD OF MAXIMUM LIKELIHOOD, AND BAYESIAN ESTIMATION. BECAUSE OF THE LARGE NUMBER OF PARAMETERS INVOLVED IN MULTIVARIATE TIME SERIES MODELS, THESE PROCEDURES ARE MORE DIFFICULT TO IMPLEMENT IN THE MULTIVARIATE CASE. (ALTHOUGH THE CONCEPTUAL APPROACHES (SUCH AS MAXIMUM LIKELIHOOD) ARE THE SAME, THEY ARE MORE DIFFICULT TO IMPLEMENT IN THE MULTIVARIATE CASE BECAUSE THE NUMERICAL METHODS USED TO IMPLEMENT THE METHODS MAY CONVERGE SLOWLY (OR NOT AT ALL) AS THE NUMBER OF PARAMETERS INCREASES.) IT IS THE PURPOSE OF THIS PRESENTATION TO DESCRIBE BASIC CONCEPTS, NOT DETAILED COMPUTATIONAL PROCEDURES. FOR THIS REASON, ESTIMATION METHODS WILL NOT BE DESCRIBED FOR MULTIVARIATE MODELS, EXCEPT FOR A BRIEF DISCUSSION OF LEAST-SQUARES ESTIMATION, TO FOLLOW. SEE THE CITED REFERENCES ON MULTIVARIATE TIME SERIES ANALYSIS FOR DISCUSSION AND DETAILS.
LEAST-SQUARES ESTIMATION FOR MULTIVARIATE MODELS
THIS SECTION PRESENTS INFORMATION ABOUT THE METHOD OF LEAST-SQUARES, IN THE ESTIMATION OF PARAMETERS OF A MULTIVARIATE REGRESSION MODEL, AND, IN PARTICULAR, OF A VECTOR AUTOREGRESSIVE MODEL. THE PRESENTATION FOLLOWS THE NOTATION OF GREENE OP. CIT., pp. 292-296 (AND IS SIMILAR TO THE PRESENTATION IN ZIVOT AND WANG pp. 364-366, AND, FOR A SPECIAL CASE, TO THE PRESENTATION IN TSAY pp. 44-47).
LET US CONSIDER THE CASE OF AN UNRESTRICTED SYSTEM OF M LINEAR REGRESSION EQUATIONS:
![]()
WHERE yi
DENOTES THE i-th DEPENDENT VARIABLE, M DENOTES THE NUMBER OF DEPENDENT
VARIABLES, ki DENOTES THE NUMBER OF REGRESSORS IN THE i-th EQUATION,
K = ![]() , T DENOTES THE NUMBER OF OBSERVATIONS, yi
IS (T x 1), Xi is (T x ki), βi is (K x 1), AND εi is (T x 1). WE ASSUME STRICT EXOGENEITY OF Xi,
, T DENOTES THE NUMBER OF OBSERVATIONS, yi
IS (T x 1), Xi is (T x ki), βi is (K x 1), AND εi is (T x 1). WE ASSUME STRICT EXOGENEITY OF Xi,
![]()
AND HOMOSCEDASTICITY,
![]()
THE ERROR TERMS εi ARE CORRELATED ACROSS THE EQUATIONS (VARIABLES), BUT OVER OBSERVATIONS (WHICH, IN A TIME-SERIES APPLICATION, IS TIME):
![]()
THIS MODEL IS CALLED A SEEMINGLY UNRELATED REGRESSIONS (SUR) MODEL.
THE M EQUATIONS MAY BE STACKED TO FORM A GENERALIZED REGRESSION MODEL (OR “GIANT” REGRESSION MODEL):
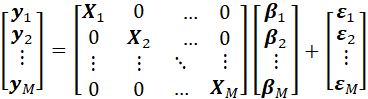
OR
![]()
WHERE y IS (MT x 1), X IS (MT x K), β IS (K x 1) AND ε IS (MT x 1).
FOR EACH OF THE i OBSERVATIONS, THE M x M COVARIANCE MATRIX OF THE MODEL ERROR TERM IS
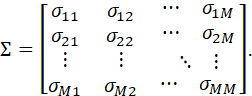
WE HAVE
![]()
AND
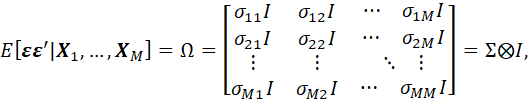
HENCE
![]()
DENOTING THE ij-th ELEMENT OF Σ-1 BY σij, THE GENERALIZED LEAST-SQUARES ESTIMATOR OF β IS GIVEN BY:
![]()
IT CAN BE SHOWN THAT IN THE CASE IN WHICH THE SAME REGRESSORS (EXPLANATORY VARIABLES) ARE USED IN EVERY EQUATION (WHICH IS THE CASE FOR A VAR), OR THE REGRESSORS IN ONE EQUATION ARE A SUBSET OF THOSE IN ANOTHER, THAT THIS REDUCES TO
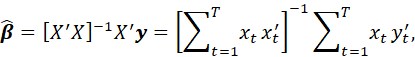
WHERE, IN THIS EXPRESSION, THE MATRIX X IS THE COMMON VALUE OF THE MATRICES Xi, NOT THE “GIANT” MATRIX X GIVEN EARLIER. THIS EXPRESSION DOES NOT INVOLVE THE COVARIANCE MATRIX Σ. THIS MEANS THAT THE GENERALIZED LEAST-SQUARES ESTIMATE IS IDENTICAL TO THE ORDINARY LEAST-SQUARES ESTIMATE.
IT CAN ALSO BE SHOWN (SEE GREENE) THAT THE PARAMETER ESTIMATES FOR EACH REGRESSION EQUATION (CORRESPONDING TO EACH DEPENDENT VARIABLE) CAN BE OBTAINED BY APPLYING OLS TO EACH EQUATION SEPARATELY. (THIS SAME RESULT HOLDS IF THE DEPENDENT VARIABLES ARE UNCORRELATED.)
TESTS OF MODEL ADEQUACY
MODELS ARE TESTED FOR ADEQUACY BY TESTING WHETHER THE MODEL RESIDUALS ARE WHITE, AND BY TESTING THE SIGNIFICANCE OF MODEL PARMATERS. FOR MULTIVARIATE MODELS THESE TESTS ARE ANALOGOUS TO THOSE USED FOR UNIVARIATE MODELS.
MEASURES OF MODEL EFFICIENCY
THE EFFICIENCY OF MODELS IS ASSESSED USING THE SAME CRITERIA AS WERE USED IN THE UNIVARIATE CASE, I.E., THE AIC, THE BIC AND THE HQC.
IMPULSE RESPONSE
AS WAS DISCUSSED EARLIER, ESTIMATION OF AN IMPULSE RESPONSE OF ONE VARIABLE ON ANOTHER (THE RESPONSE VARIABLE) IS REASONABLE ONLY IF THE PULSED VARIABLE IS UNCORRELATED WITH THE OTHER MODEL VARIABLES (I.E., OTHER THAN THE RESPONSE VARIABLE). IN GENERAL, THE ERROR TERMS IN A MULTIVARIATE MODEL ARE CORRELATED. TO ESTIMATE REASONABLE IMPULSE RESPONSES, IT IS DESIRABLE TO TRANSFORM THE MODEL SO THAT THE MODEL ERROR TERMS ARE UNCORRELATED (ORTHOGONAL). THIS TOPIC WAS ADDRESSED EARLIER IN THE SECTION ON DESCRIPTORS OF MULTIVARIATE TIME SERIES.
FORECASTING (UNCONDITIONAL VS. CONDITIONAL)
THE ISSUE OF MAKING UNCONDITIONAL VS. CONDITIONAL FORECASTS WAS ADDRESSED IN THE PRECEDING SECTION ON MODEL IDENTIFICATION.
FORECAST ERROR VARIANCE DECOMPOSITION
WHEN A MODEL INCLUDES MULTIPLE VARIABLES, IT IS OF INTEREST TO ESTIMATE THE PORTION OF THE FORECAST ERROR VARIANCE IN ONE VARIABLE THAT IS ASSOCIATED WITH EACH OF THE OTHER VARIABLES. SINCE THE MODEL VARIABLES ARE CORRELATED, THE CONTRIBUTION OF A VARIABLE TO THE TOTAL ERROR VARIANCE DEPENDS ON WHAT OTHER VARIABLES ARE INCLUDED IN THE MODEL. A STANDARD PROCEDURE IS TO ORDER THE MODEL VARIABLES AND ESTIMATE THE EXTENT TO WHICH THE FORECAST ERROR VARIANCE CHANGES AS EACH VARIABLE IS REMOVED FROM THE MODEL. OBVIOUSLY, THE CONTRIBUTION OF A PARTICULAR VARIABLE TO THE TOTAL FORECAST ERROR VARIANCE WILL DEPEND ON THE ORDER IN WHICH THE VARIABLES ARE REMOVED.
PROCESS CONTROL
A TIME SERIES MODEL MAY BE USED FOR PROCESS CONTROL. THE METHODS OF PROCESS CONTROL ARE SIMILAR TO THOSE IN FORECASTING, EXCEPT FOR THE FACT THAT THE FORECAST IS DESIRED FOR THE SITUATION IN WHICH FORCED CHANGES ARE MADE IN THE CONTROL VARIABLES. TO USE A MODEL TO ESTIMATE THE CHANGES THAT FORCED CHANGES IN CERTAIN VARIABLES WILL CAUSE IN OTHER VARIABLES REQUIRES THAT THE MODEL BE ESTIMATED FROM A CAUSAL MODEL (SUCH AS AN EXPERIMENTAL DESIGN, IN WHICH FORCED CHANGES ARE MADE IN THE CONTROL VARIABLES).
SOME ASPECTS OF PROCESS CONTROL WERE DISCUSSED EARLIER, IN THE SECTION ON TRANSFER-FUNCTION MODELS. FOR DISCUSSION OF OPTIMAL FEEDBACK CONTROL USING ARMAX MODELS, SEE REINSEL OP. CIT. (2ND ED), pp. 280-285.
AS MENTIONED, THE TOPIC OF OPTIMAL CONTROL IS NOT ADDRESSED IN THIS PRESENTATION, WHICH FOCUSES ON ESTIMATION AND FORECASTING. ONCE A VALID MULTIVARIATE TIME SERIES MODEL HAS BEEN DEVELOPED, THE TECHNIQUES OF OPTIMIZATION MAY BE USED TO DETERMINE OPTIMAL CONTROL SCHEMES (PROVIDED APPROPRIATE EXOGENEITY CONDITIONS ARE SATISFIED). DETERMINATION OF SUCH CONTROL SCHEMES REQUIRES FACILITY IN THE USE OF CONSTRAINED OPTIMIZATION TECHNIQUES, WHICH MAY BE IMPLEMENTED USING MODELING AND OPTIMIZATION SOFTWARE PACKAGES SUCH AS GAMS.
ALTERNATIVE REPRESENTATIONS: STATE SPACE, KALMAN FILTER
THE PRECEDING SECTIONS HAVE DESCRIBED TIME SERIES ANALYSIS FOR STATIONARY PROCESSES IN THE CASE OF NO MEASUREMENT ERROR AND TIME-INVARIANT PARAMETERS. THEORY IS AVAILABLE FOR ANALYSIS OF TIME SERIES IN THE CASE OF TIME-VARYING PARAMETERS AND MEASUREMENT ERROR. THIS THEORY INCLUDES METHODS SUCH AS ARCH, GARCH, STATE-SPACE MODELS, AND THE KALMAN FILTER. FOR DISCUSSION OF THESE TOPICS, SEE THE CITED REFERENCES. FOR DETAILED DISCUSSION OF KALMAN FILTER SEE
DURBIN, J. AND S. J. KOOPMAN, TIME SERIES ANALYSIS BY STATE SPACE METHODS, 2ND ED. (OXFORD UNIVERSITY PRESS, 2012).
ALTERNATIVES TO THE GAUSSIAN DISTRIBUTION; COPULAS
[NOTE: THE MATERIAL PRESENTED IN THIS SECTION IS NOT INCLUDED IN THE PRESENTATION ON CONTINUOUS MULTIVARIATE ANALYSIS.]
MUCH OF THE THEORY OF MULTIVARIATE TIME SERIES IS BASED ON THE ASSUMPTION THAT THE MODEL RESIDUALS ARE NORMALLY DISTRIBUTED, OR GAUSSIAN. A NORMAL DISTRIBUTION IS CHARACTERIZED BY ITS MEAN VECTOR AND COVARIANCE MATRIX. FOR THIS DISTRIBUTION, THE CORRELATIONAL STRUCTURE IS VERY SIMPLE – IT IS SYMMETRIC AND ELLIPTICAL IN NATURE. IT IS COMPLICATED TO DESCRIBE, REQUIRING THE SPECIFICATION OF A MATRIX CONTAINING K x K PARAMETERS (THE CORRELATIONS), WHERE K IS THE NUMBER OF COMPONENTS OF THE MULTIVARIATE RESPONSE VARIABLE.
IN SOME APPLICATIONS, THE GAUSSIAN ASSUMPTION IS NOT APPROPRIATE. IN FINANCE, FOR EXAMPLE, THE BEHAVIOR OF INVESTORS IS MUCH MORE HIGHLY CORRELATED IN A FALLING MARKET (DOWNSIDE, CRISIS, PANIC) THAN IN A RISING MARKET. SUCH BEHAVIOR IS AT DIFFERENCE WITH THE SYMMETRIC NATURE OF THE GAUSSIAN CORRELATION SPECIFICATION. IN FINANCE APPLICATIONS, IT IS ALSO DESIRABLE TO REPRESENT CORRELATION OF HIGH-DIMENSIONAL RANDOM VARIABLES BY ONE OR A FEW PARAMETERS, NOT BY ALL OF THE ENTRIS OF A CORRELATION MATRIX.
A MEANS FOR ADDRESSING THESE ISSUES IS PROVIDED BY COPULA THEORY. THIS SECTION DESCRIBES SOME BASIC CONCEPTS OF COPULA THEORY. FOR A READABLE DISCUSSION OF COPULA THEORY, SEE THE WIKIPEDIA ARTICLE POSTED AT https://en.wikipedia.org/wiki/Copula_(probability_theory) .
COPULAS HAVE BEEN WIDELY USED IN MATHEMATICAL FINANCE TO MODEL AND MINIMIZE “TAIL RISK” (RISK ASSOCIATED WITH RARE EVENTS, ASSOCIATED WITH THE TAILS OF A PROBABILITY DENSITY) AND PORTFOLIO OPTIMIZATION APPLICATIONS. THEY ARE USED IN RISK MANAGEMENT, PORTFOLIO MANAGEMENT, PORTFOLIO OPTIMIZATION AND DERIVATIVES PRICING.
A COPULA IS A MULTIVARIATE PROBABILITY DISTRIBUTION FOR WHICH THE MARGINAL PROBABILITY DISTRIBUTION OF EACH VARIABLE IS UNIFORM. SKLAR’S THEOREM STATES THAT ANY MULTIVARIATE JOINT DISTRIBUTION CAN BE WRITTEN IN TERMS OF UNIVARIATE MARGINAL DISTRIBUTION FUNCTIONS AND A COPULA WHICH DESCRIBES THE DEPENDENCE STRUCTURE AMONG THE VARIABLES.
SUPPOSE THAT (X1, X2,…,Xd) IS A RANDOM VECTOR WITH CONTINUOUS MARGINAL CUMULATIVE DISTRIBUTION FUNCTIONS (CDFs) Fi(x) = Pr[Xi <= x]. THE RANDOM VECTOR
(U1, U2,…,Ud) = (F1(X1),F(X2),…,Fd(Xd))
HAS UNIFORM MARGINAL DISTRIBUTIONS.
THE COPULA OF (X1,…Xd) IS DEFINED AS THE JOINT CDF OF (U1,…,Ud):
C(u1, …, ud) = Pr[U1 <= u1,…,Ud <= ud].
THE COPULA CONTAINS ALL OF THE INFORMATION ABOUT THE DEPENDENCE STRUCTURE AMONG THE COMPONENTS OF (X1,…,Xd), AND THE MARGINAL CDFs Fi CONTAIN ALL OF THE INFORMATION ABOUT THE MARGINAL DISTRIBUTIONS.
THE REVERSE OF THESE STEPS CAN BE USED TO GENERATE PSEUDO-RANDOM SAMPLES FROM GENERAL CLASSES OF MULTIVARIATE PROBABILITY DISTRIBUTIONS. GIVEN A PROCEDURE TO GENERATE A SAMPLE (U1,…,Ud) FROM A COPULA DISTRIBUTION, THE DESIRED SAMPLE CAN BE CONSTRUCTED AS
(X1,…,Xd) = (F1-1(U1),…,Fd-1(Ud)).
THE CORRESPONDING COPULA FUNCTION IS
C(u1,…,ud) = Pr[X1 <= F1-1(u1),…,Xd <= Fd-1(ud)].
SKLAR’S THEOREM STATES THAT EVERY MULTIVARIATE CDF
H(x1,…,xd) = Pr[X1 <= x1,…,Xd <= xd]
OF A RANDOM VECTOR (X1,…,Xd) CAN BE EXPRESSED IN TERMS OF ITS MARGINALS Fi(x) = Pr[Xi <= xi] AND A COPULA C:
H(x1,…,xd) = C(F1(x1),…,Fd(xd)).
IF THE MULTIVARIATE DISTRIBUTION HAS A DENSITY h, THEN
H(x1,…,xd) = c(F1(x1),…,Fd(xd)) f1(x1)…fd(xd),
WHERE c IS THE DENSITY OF THE COPULA.
DETAILED EXAMPLE OF A MULTIVARIATE TIME SERIES ANALYSIS APPLICATION
THE CITED REFERENCES (ESPECIALLY BJRL, TSAY MTSA AND LÜTKEPOHL) PROVIDE DETAILED EXAMPLES OF ALL ASPECTS OF MULTIVARIATE TIME SERIES ANALYSIS. FOR A COMPACT SUMMARY OF KEY ASPECTS, THE ARTICLE VECTOR AUTOREGRESSIONS BY JAMES H. STOCK AND MARK W. WATSON (2001), POSTED AT INTERNET WEBSITE https://pubs.aeaweb.org/doi/pdfplus/10.1257/jep.15.4.101 IS RECOMMENDED.
5. TIME SERIES ANALYSIS SOFTWARE
SOME STANDARD GENERAL-PURPOSE STATISTICAL SOFTWARE PACKAGES, SUCH AS SAS AND STATA, INCLUDE MODULES FOR ESTIMATING AND ANALYZING VECTOR AUTOREGRESSIVE (VAR) TIME SERIES MODELS (SPSS DOES NOT). FOR VECTOR AUTREGRESSIVE MOVING AVERAGE MODELS, R SOFTWARE IS AVAILABLE. SOFTWARE SOURCES AND PROCEDURES FOR USING THIS SOFTWARE ARE DESCRIBED IN THE CITED REFERENCE TEXTS. FOR THE MAJOR REFERENCES, LINKS TO R SOFTWARE ARE AS FOLLOWS:
THE MAIN WEBSITE FOR THE R PROJECT IS https://www.r-project.org/ . SEE DISCUSSION ON pp. 17-18 FOR DETAILS. SEE PACKAGES TSA, MTS, astata, stats.
THE WEBSITE FOR THE BOOK TSAY, MULTIVARIATE TIME SERIES ANALYSIS WITH R AND FINANCIAL APPLICATIONS (WILEY, 2014) IS http://faculty.chicagobooth.edu/ruey.tsay/teaching/mtsbk/ .
THE WEBSITE FOR THE BOOK TSAY, ANALYSIS OF FINANCIAL TIME SERIES (WILEY, 2010) IS http://faculty.chicagobooth.edu/ruey.tsay/teaching/fts3/ .
THE WEBSITE FOR THE BOOK LÜTKEPOHL, NEW INTRODUCTION TO MULTIPLE TIME SERIES ANALYSIS (SPRINGER, 2006) IS http://www.jmulti.de/ .
THE WEBSITE FOR THE BOOK (ON UNIVARIATE TIME SERIES ANALYSIS) BY CRYER AND CHAN, TIME SERIES ANALYSIS WITH APPLICATIONS IN R (SPRINGER, 2008) IS http://homepage.divms.uiowa.edu/~kchan/TSA.htm .
FOR BACKGOUND ON R AND S, SEE
VENABLES, W. N., AND B. D. RIPLEY, MODERN APPLIED STATISTICS WITH S, 4TH ED. (SPRINGER, 2002)
ADLER, JOSEPH, R IN A NUTSHELL 2ND ED. (O’REILLY, 2012)
CRAWLEY, MICHAEL J., THE R BOOK, (WILEY, 2007)
SAWITZKI, GÜNTER, COMPUTATIONAL STATISTICS, AN INTRODUCTION TO R (CRC PRESS, 2009)
CORNILLON, PIERRE-ANDRÉ, R FOR STATISTICS (CRC PRESS, 2012)
ZIVOT, ERIC AND JIAHUI WANG, MODERN FINANCIAL TIME SERIES WITH S-PLUS 2ND ED., (SPRINGER, 2006). POSTED AT INTERNET WEBSITE http://faculty.washington.edu/ezivot/econ589/manual.pdf .
FndID(207)
FndTitle(MULTIVARIATE TIME SERIES ANALYSIS: LECTURE NOTES)
FndDescription(MULTIVARIATE TIME SERIES ANALYSIS: LECTURE NOTES)
FndKeywords(time series analysis; multivariate analysis; multivariate time series analysis; stochastic processes; statistics course; short course)