Subtractive Overlapping Island Defense with Imperfect Interceptors
I. Introduction
A. Formulation of the Problem
The objective of this study is to examine the effect of relaxing the assumption of perfect interceptors on damage from nuclear attack, in the case of subtractive overlapping island defense. As such, this effort is an extension of the work described in Lambda Special Report 4 (Reference 1), which analyzed the imperfect interceptor situation in the terminal defense case.
This section will define the problem of subtractive overlapping island defense with imperfect interceptors, and the next section will summarize the results of the study.
Subtractive Overlapping Island Defense
Let us consider a collection of n targets and a collection of N batteries of interceptors. The interceptors at a battery are assumed to be able to intercept weapons aimed at any targets within a specified flyout radius, R, of the battery. The flyout radius is assumed to be the same for all interceptors at all batteries. The circular defense zone around a battery defined by the flyout radius is called an "island." A particular target may be defended by interceptors from any battery not farther away from it than the flyout radius. Whenever there are two or more batteries capable of defending the targets in common, we say that their islands "overlap."
A "subtractive" defense of overlapping islands is a defense such that weapons fired at a target are intercepted as they arrive by interceptors from any battery whose island includes the target, until all interceptors from those batteries are exhausted.
Note that if the defender uses a subtractive island defense, he is actually letting the attacker determine the deployment of interceptors to targets within each island. The attacker controls this deployment by his firing order. For example, in the nonoverlapping case, if there are Yj interceptors allocated by the defender to zone j, then the attacker's allocation of his first Yj weapons to targets in the zone determines and is in fact the same as the allocation of the Yj interceptors to targets. Of course, the defender determines the value of Yj. In the case of overlapping islands, the defender can determine which battery intercepts a weapon aimed at a target defended by more than one battery. Because of this, the attacker must attack targets in order of the number of zones covering them, in order to have full control over the deployment of interceptors to targets.
An "optimal" subtractive overlapping island defense against a specified total number of weapons is one in which the defender determines his allocations of interceptors to zones so as to minimize the damage caused by the attack.
It is of interest to note the difference between subtractive overlapping island defense and terminal defense. (Note: This report deals exclusively with area defense. Area interceptors can be deployed, however, either in a subtractive mode, or in a terminal mode (fixed number of area interceptors associated with each target). The latter deployment of area interceptors is what is meant in this report by "terminal defense.") In terminal defense, area interceptors are deployed directly to targets, and can defend only the target with which they are associated. Terminal defense plays an important role in this report, since the damage from terminal defense is shown to be closely related to the damage from subtractive overlapping island defense.
Imperfect Interceptors
The problem of determining an optimal defense becomes more difficult if we allow for the possibility of "imperfect interceptors." By an imperfect interceptor, we mean one whose probability of destroying a weapon at which it is fired is less than unity. In this report, the term "interceptor" can in fact refer to a salvo of interceptors; the interceptor or interceptor salvo is characterized by its reliability, or probability of destroying a weapon at which it is fired.
We further assume that the firing of interceptors is not reprogrammable, i.e., a second interceptor cannot be fired at a weapon if the first interceptor fails. However, for defenses involving large numbers of interceptors, the results of this study can be used to provide good approximate results for the reprogrammable case. Suppose, for example, that we have a total of Y interceptors of reliability κ, and that through reprogramming, the expected number of weapons which the defense can intercept becomes Y', and the probability of successful interception becomes κ'. Then the results of this study can be applied, using Y' interceptors of reliability κ'.
The Problem
The objective of this study, as noted above, is to determine the nature of subtractive overlapping island defense in the case in which interceptors are imperfect. This objective will be accomplished by examining the effect of changing interceptor kill probability, κ, on the damage from the optimal subtractive overlapping defense.
B. Summary of Results
In the perfect interceptor case (interceptor kill probability κ = 1), the optimal subtractive overlapping island defense is determined. For κ < 1, the exact solution is not found, but a close approximate solution, and "tight" bounds on the exact solution, are determined.
TO BE DONE: When completed, this report will estimate the expected damage for optimal attack and defense using subtractive overlapping island defense, for a national missile defense system protecting the United States. Work is currently in progress to develop an up-to-date US city list that contains population and geographic-size data.
In general, the expected damage for subtractive defense is greater than that for optimal terminal defense. The reason for this is that, by employing a subtractive defense, the defender is allowing the attacker to determine the allocation of interceptors to targets within a defense zone, by means of his (the attacker's) firing order. This begs the question: Why would anyone use a subtractive defense, if the optimal terminal defense is better? The reason is that this result holds under the assumption that both the attacker and the defender know the total weapon and interceptor inventories. In an actual attack, this assumption may not apply. It is because the attack size may not be known that the defender employs a subtractive defense. An example will clarify this. In a large attack against the US, the US may (rationally, in an optimal defense) allocate all interceptors near Washington, DC, to defend that city, and choose not to defend nearby Baltimore (or other nearby cities) at all. If, however, a single attacking missile is detected, and it is aimed at Baltimore, the US may decide that the attack is a single missile from a "rogue nation," rather than a massive attack from a significant nuclear power. In this case, it makes sense to save Baltimore by firing an interceptor from the Baltimore-Washington defense zone at the attacking missile. If it turns out that a single missile was all that was involved in the attack, this was a desirable outcome -- Baltimore is saved. If, however, it turns out that this missile was simply the first one of a massive attack against the US, then firing an interceptor in defense of Baltimore will simply mean that there is one less interceptor available to defend Washington, and the defense will not be optimal.
Sections II and III of this report provide technical descriptions of optimal attacks, and may be skipped by the reader not interested in examining technical detail.
II. Optimal Subtractive Overlapping Island Defense with Imperfect Interceptors: Mathematical Formulation of the Problem
We shall now present a mathematical formulation of the problem of determining the optimal subtractive overlapping island defense damage in the case of imperfect interceptors.
A. Notation
Before defining an optimal subtractive overlapping island defense, we shall introduce some further notation. To recapitulate, we have already defined
n = total number of targets;
N = total number of interceptor batteries;
R = interceptor flyout radius;
Y = total number of interceptors;
Yj = total number of interceptors allocated to battery j (zone j);
κ = interceptor kill probability (probability that an interceptor successfully destroys a weapon at which it is fired); interceptor kill probability.
Further, we define:
X = total number of weapons;
xij = number of weapons allocated to the i-th target of j-th zone;
yij = number of interceptors deployed at i-th target of j-th zone;
nj = total number of targets in j-th zone;
y = (y11,y21,…,yn1 1,…,y1N,y2N,…,ynN N)';
x = (x11,x21,…,xn1 1,…,x1N,x2N,…,xnN N)';
Y = (Y1,Y2,…,YN)'; note that Yj = Σ(i) yij, where Σ(.) denotes the summation operator;
Pij = population of i-th target of j-th zone.
The symbol Σ(.) denotes the summation operator, where the arguments specifies the index and range (or indices and ranges) of summation. For example, Σ(i) yij denotes the sum of yij over the index i; Σ(i:1,t) yij denotes the sum over i from 1 to t; Σ(i,j) denotes the sum over indices i and j, and so on. Also note that the word processor used to produce this article does not enable subscripts within subscripts, so that, for example, in the term ynN N the first subscript stands for nN, not nN.
Continuing, we define Hij(xij,yij) to be the damage to the i-th target of the j-th zone if xij weapons and yij interceptors are placed on that target. This damage is assumed to be independent of the x's and y's of other targets. The total damage,
Σ(i,j) H(ij(xij,yij)) ,
is denoted by H(X,Y). We shall also denote this damage by H(x,y) in the case of terminal defense, and by H(x,Y) in the case of subtractive overlapping island defense.
B. Optimal Subtractive Overlapping Island Defense
We shall now define what we mean by the optimal subtractive overlapping island defense. We assume that the attacker and defender both know each other's total force sizes, X and Y. We assume that the attacker "moves last," i.e., he determines his allocations x and y of weapons and therefore interceptors to targets after observing the defender's allocation Y of interceptors to zones. Whatever the defense, the attacker is assumed to allocate his weapons to targets so as to maximize fatalities. The attacker is assumed to know the number and deployment of interceptors, the flyout radius of the interceptors, the interceptor kill probability, κ, the type of defense (subtractive overlapping island or terminal), the firing doctrine (one-on-one), and, of course, the population and k-factor of each target. The defender is assumed to know the total attack size and the weapon characteristics (yield, CEP, reliability). The defender is assumed to allocate interceptors so as to minimize the total damage that the attacker can cause. To maximize damage, the attacker will choose strategies x*(Y) and y*(Y) such that
H(x*(Y),y*(Y)) = max(x,y) H(x,y) ,
where the notation max(x,y) denotes maximization over x and y of the function that follows (in this case, H(x,y)).
To minimize damage, the defender will choose a strategy Y* such that
H(x*(Y*),y*(Y*)) = min (Y) max(x,y) H(x,y) ,
where max(Y) denotes maximization over Y of the expression that follows.
The resource constraints on the above optimization are
Σ(j) Yj = Y
Σ(i,j) Yij = Y
Σ(i) yij = Yj
yij ≥ 0
Σ(i,j) xij = X
xij ≥ 0
for all i,j.
The "subtractive" constraints are that for each j, we have
either xij ≤ yij for all i
or xij ≥ yij for all i .
We shall write the above expressions and constraints as
H(x*,Y*) = (min(Y) | Σ(j) Yj = Y, Yj ≥ 0) (max(y) | Σ(i,j) yij = Y, Σ(i) yij = Yj, yij ≥ 0)
(max(x) | Σ(i,j) xij = X, xij ≥ 0, S) H(x,y)
where S denotes the subtractive condition
for each j, either xij ≥ yij for all i
or xij ≤ yij for all i .
The optimal defense is thus the "minimax" defense.
The above optimization problem is difficult to solve for interceptor reliabilities less than unity. Although solving this optimization problem might appear to be the most direct method of determining the relationship of optimal subtractive overlapping island defense damage to interceptor kill probability, it is in fact an inefficient approach. Instead, lower bounds to the optimal damage curve are found, in terms of optimal terminal defense damage curves. These lower bounds prove sufficient to indicate the effect of interceptor kill probability on the optimal subtractive overlapping island defense damage curve. The advantage of finding a solution in terms of optimal terminal defenses is that the optimal terminal defense problem has already been solved (Reference 1) and a computer program is available to perform analysis for specified target sets. Even if a direct solution could have been found to the above optimization problem, which is not the case, additional computer programming would be required to implement it. Another benefit of the lower-bound approach is that it showed the theoretical relationship between the optimal subtractive overlapping island and optimal terminal defense damage curves.
III. Optimal Terminal Defense with Imperfect Interceptors: A Review
Since the lower bound to be determined for the optimal subtractive overlapping island defense damage curve involves the optimal terminal defense damage curve, we shall review the latter in this section. See Reference 1 for a complete description of the theory.
As we noted earlier, terminal defense can be considered a limiting form of subtractive overlapping island defense, one in which each defense zone contains but a single target. Since the zone concept is hence redundant, we shall drop the subscript j and refer to the weapon and interceptor allocations simply as
x = (x1,...,xn)'
and
y = (y1,...,yn)' .
As in the overlapping island case, an optimal terminal defense is defined to be one in which the attack and defense allocations x* and y* are chosen so that
H(x*,y*) = min(y) max(x) H(x,y)
subject to the constraints Σ(i) yi = Y, yi ≥ 0, Σ(i) xi = X, xi ≥ 0. We shall also write this expression as
H(x*,y*) = (min(y) | Σ(i) yi = Y, yi ≥ 0) (max(x) | Σ(i) xi = X, xi ≥ 0) H(x,y) .
The optimal defense is thus the "minmax" defense.
We shall now describe the nature of the solution to this optimization problem. Figure 1 illustrates the damage function of an individual target in the case of the minmax terminal defense. The attacker determines x1 and x2, and the defender chooses y on each target so that the tangents to the damage curve at x1 and x2 coincide, and the slope, L = L(Y), of this tangent is the same on all targets. (Not illustrated are those targets whose no-defense damage functions are everywhere of slope less than L; such targets are neither defended nor attacked.) If the initial portion of the damage curve is everywhere of slope less than L, then x1 = 0, and the tangent to the damage curve at x2 must pass through the origin.
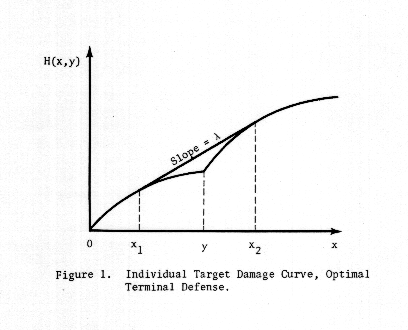
Figure 2 illustrates the total damage curve for
the minmax terminal defense. The curve is best described in terms of two
attack levels, Xmin(Y) and Xmax(Y), which depend on the
total defense size, Y. For attacks of size X < Xmin(Y), damage
occurs only through "leakage"; there are more interceptors than
weapons on every target. The level at which each target is attacked is such
that the slope (L1 > L) of the target damage curve at that point
is the same for all targets. At X = Xmin(Y), all targets are
attacked at the x1 level. For X between Xmin(Y) and Xmax(Y),
some targets are attacked at the x1 level, and the remainder at the
x2 level. At X = Xmax(Y), all targets are attacked at
the x2 level. Up to the attack level Xmax(Y), the
defense need not change (it is in fact somewhat arbitrary for attack levels
below Xmin(Y)). As X increases above Xmax(Y), the
defender defends fewer and fewer targets, until only one target is defended.
The level at which each target is attacked is such that the slope (L2
< L) of the target damage curve at that point is the same for all targets.
Between Xmin(Y) and Xmax(Y) the concave hull of the total
damage curve is linear, of slope L.

IV. Lower Bounds to the Optimal Subtractive Overlapping Island Defense Damage Curve and Its Concave Hull
As was mentioned in the preceding section, the approach used to determine the relationship of the optimal subtractive overlapping island defense damage curve to interceptor kill probability involves the use of certain lower bounds. These bounds are derived in Appendix A.
The most important bound found is a lower bound to the concave hull of the optimal damage curve. The lower bound is in fact the concave hull of the optimal terminal defense damage curve (for the same interceptor kill probability). The optimal damage curve coincides with its hull over the curved portions at the beginning and end of the damage curve, but the damage curve drops below the hull along the central, linear portion. The damage curve reaches the hull along the linear portion (M - 1)M! times, where M is the number of disconnected regions of connected defense zones (islands). Since the attacker "moves last," he can choose to attack only at attack levels for which the damage is on the hull, hence the importance of the lower bound to the hull.
In the case of perfect interceptors (κ = 1), it is shown in Appendix A that the hull of the optimal subtractive overlapping island defense damage curve coincides with the hull of the optimal terminal defense damage curve. The latter is known from Lambda Special Report 4 (Reference 1), and hence we know the hull of the optimal subtractive overlapping island defense damage curve for κ = 1.
Two lower bounds were also determined for the optimal subtractive overlapping island defense damage curve itself. The first lower bound is useful over the initial portion of the linear region of the hull, and the second, an approximate bound, is useful over the remaining portion of the linear region.
V. Application of Theoretical Results to a Specified Target Complex
TO BE DONE: Summary of section purpose and results.
A. Description of the Target Complex
TO BE DONE: A description of the city list used in the analysis. For each city, the geographic size of the city is described by a parameter known as a "k-factor." That factor appears in the damage functions used in this report.
.
B. Defenses Studied
TO BE DONE: A description of interceptor stockpile sizes, interceptor batteries (defense zone locations), interceptor kill probabilities, interceptor flyout radii. These quantities will be varied parametrically over reasonable ranges.
For the minmax, or optimal, defense, it is assumed that the defender knows the total attack size.
In the analysis that follows, a number of different interceptor allocations are studied. These defenses will be referred to by the indicated uppercase Latin letters.
A*: Optimal subtractive overlapping island defense. Interceptors are allocated to the 30 batteries so as to minimize the total damage from a specified attack size. The allocation is a function of the attack size and the interceptor flyout radius (R).
A': Proportional-to-value subtractive overlapping island defense. Interceptors are allocated to each of the 30 batteries proportional to the total population of the defense zone (island) covered by the battery, regardless of overlap among zones. The allocation hence depends on the flyout radius, but is not a function of the attack size.
B*: Optimal terminal defense. Interceptors are allocated to targets of zones so as to minimize the total damage from specified attack size. The allocation depends on the attack size and the flyout radius.
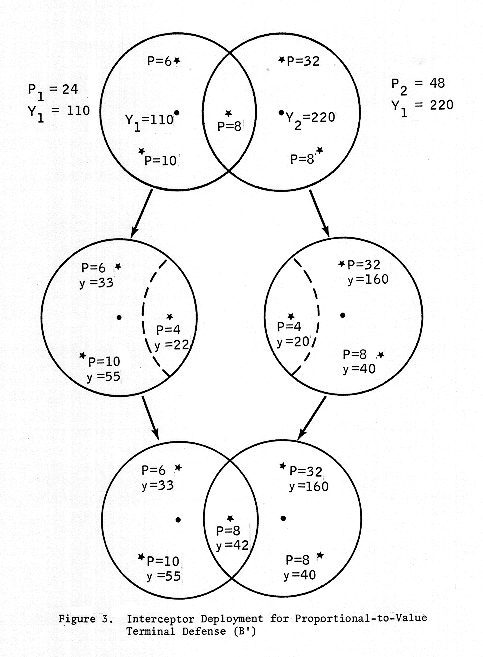
B': Proportional-to-value terminal defense. Allocate interceptors to batteries as in defense A' (proportional to population of zone defended by battery). Deploy interceptors of a zone to each target of the zone proportional to the population of the target divided by the number of zones covering it. The deployment is not a function of the attack size. See Figure 3 for an example of a B' defense deployment. Note that this definition of proportional-to-value terminal defense differs from the usual definition, in which the number of interceptors allocated to each defended target is proportional to the population of the target. The nonstandard proportional-to-value defense defined here is used because it is felt that its damage curve provides a better approximation to the optimal subtractive overlapping island defense damage curve than the damage curve of the usual proportional-to-value defense. (Of course, if we were in general primarily interested in approximating the optimal terminal defense damage curve, then the usual proportional-to-value defense would be more appropriate.) As the flyout radius, R, decreases to the point (5 n.m.) at which each island contains but a single target, then the two definitions yield the same defense.
C. Nature of the Attack
Whatever the defense, the attacker is assumed to allocate his weapons to targets so as to maximize fatalities. The attacker is assumed to know the number and deployment of interceptors, the flyout radius of the interceptors, the interceptor kill probability, κ, the type of defense (subtractive overlapping island or terminal), the firing doctrine (one-on-one), and, of course, the population and k-factor of each target. We assume that there are no penetration aids ("penaids").
TO BE DONE: Assumptions will be made about the yield (in megatons, MT), geographic variability of hitting the target (the CEP, or circle of equal probability), and the reliability of the weapons. These quantities are reflected in the damage function through the k-factor (mentioned above as a parameter describing the geographic size of a city). For each city of the city list, a nominal k-factor will be specified that reflects expected damage from a particular ("nominal") size weapon (yield and CEP). A formula will be determined to determine k-factors for weapons other than nominal.
D. Form of the Damage Function
An "exponential" damage function was used for this analysis. This damage function is described in Appendix B, which also presents a comparison of the exponential damage function to the "square root" damage function.
E. Sensitivity of Damage Curves to Attack Assumptions
TO BE DONE: This analysis will show the effect of varying weapon yield and CEP in the no-defense case.
F. Lower Bounds to Optimal Subtractive Overlapping Island Defense Damage Curves
TO BE DONE: This analysis will present lower bounds for the optimal subtractive overlapping island defense curve and its concave hull, for a range of flyout radii and interceptor reliabilities.
VI. Approximations to Optimal Defense
As mentioned before, determination of the exact optimal subtractive overlapping island defense is a difficult problem for interceptor reliabilities κ less than unity. Of course, for κ = 1, the hull of the optimal subtractive overlapping island defense curve (A*) is simply the hull of the optimal terminal defense curve, an easily computed curve. Nevertheless, even for κ = 1, the hull of the optimal curve is often approximated by the hull of the "proportional-to-value" subtractive overlapping island defense (A') damage curves. By a "proportional-to-value subtractive overlapping island defense," recall that we mean a defense in which interceptors are allocated to each island proportional to the total population of all targets located within the island, regardless of the overlap among islands.
TO BE DONE: This analysis will examine the nature of the proportional-to-value approximation in the case of perfect interceptors (κ = 1).
VII. Proportional-to-Value "Expected-Value" Approximation to the Optimal Subtractive Overlapping Island Defense Damage Curve
In the past, the hull of the optimal subtractive overlapping island defense (A*) curve for Y interceptors of reliability κ has sometimes been approximated by the hull of the proportional-to-value subtractive overlapping island defense (A'exp) hull for κY perfect interceptors.
TO BE DONE: This analysis will determine the difference between this A'exp hull and the correct optimal defense (A*) damage hull.
VIII. Proportional-to-Value Terminal Defense Approximation to the Optimal Subtractive Overlapping Island Defense Damage Curve
TO BE DONE: This analysis will show the relationship of the proportional-to-value terminal defense (B') damage curve hull to the optimal subtractive overlapping island defense (A*) damage curve hull.
IX. Conclusions
The main conclusions of this study are the following:
1. For perfect interceptors, the hull of the optimal subtractive overlapping island defense damage curve is identical to the hull of the optimal terminal defense damage curve. A program (MINMAX), developed as part of Lambda Special Report 4 (Reference 1), is available for computing this curve.
2. For interceptor kill probability κ less than one, the hull of the optimal subtractive overlapping island defense lies above the hull of the optimal terminal defense. (The reason for this is that in subtractive defense, the defender allows the attacker to determine the allocation of interceptors to targets within a zone, by means of his firing (targeting) order.) Hence, if the attacker chooses to attack only on the hull, optimal terminal defense is always better (for the defender) than optimal subtractive overlapping island defense.
3. TO BE DONE: Additional conclusions, based on the completed analysis of a US national missile defense system.
References
1. Some Problems in Ballistic Missile Defense Involving Radar Attacks and Imperfect Interceptors, ACDA/ST-145 SR 4, Lambda Special Report No. 4, Lambda Corporation, Arlington, VA May 1969. Portions of this report are reproduced as the report, Optimal Attack and Defense for a Number of Targets in the Case of Imperfect Interceptors, at Internet web site http://www.foundationwebsite.org.
Appendix A: Lower Bounds to the Optimal Subtractive Overlapping Island Defense Damage Curve
This appendix derives lower bounds to the optimal subtractive overlapping island defense damage curve and its concave hull.
I. Lower Bound for the Concave Hull of the Optimal Subtractive Overlapping Island Defense Damage Curve
This section will prove that the concave hull of the optimal subtractive overlapping island defense damage curve for a set of targets cannot be below the concave hull of the optimal terminal defense damage curve. The notation is as described in the text.
A result that is used in the derivation that follows is the following.
Lemma: If f(x) ≤ g(x) for all x, then min(x) f(x) ≤ min(x) g(x).
The variable x may be a vector, x = (x1,...,xn)' .
Proof: Let x* denote any minimizing value of g(x). Then
min(x) f(x) ≤ f(x*) ≤ g(x*) = min)x) g(x) . QED
The proof follows through for constrained minimization, as well.
We shall now determine a lower bound to the damage, HA*(X<Y), resulting from the optimal subtractive overlapping island defense.
We require xij ≥ 0, yij ≥ 0, and Yj ≥ 0 in all that follows. Regardless of overlap of defense zones, and regardless of the value of κ, the following is true.
First, we have
A(X) = (min(y) | Σ(i,j) yij = Y) ( max(x) | Σ(i,j) xij = X, S) H(x,y)
≤ (min(y) | Σ(i,j) yij = Y, Σ(i) yij = Yj) (max(x) | Σ(i,j) xij = X, S) H(x,y)
≤ (max(y) | Σ(i,j) yij = Y, Σ(i) yij = Yj) (max(x) |Σ(i,j) xij = X, S) H(x,y)
= B(X,Y).
Hence, by the lemma,
(min(Y) | Σ(j) Yj = Y) A(X) ≤ (min(Y) | Σ(j) Yj = Y) B(X,Y) . (A-1)
But
(min(Y) | Σ(j) Yj = Y) A(X) = A(X)
since A(X) does not depend on Y, hence (A-1) reduces to
A(X) ≤ (min(Y) | Σ(j) Yj = Y) B(X,Y) ,
or
A(X) = (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = X, S) H(x,y)
≤ (min(Y) | Σ(j) Yj = Y) (max(y) | Σ(i,j) yij = Y, Σ(i) yij = Yj)
(max(x) | Σ(i,j) xij = X, S) H(x,y)
= C(X) . (A-2)
Now C(X) is the damage corresponding to the optimal attack with X weapons against the optimal subtractive overlapping island defense (A*), i.e.,
C(X) = HA*(X,Y) .
Hence we have the lower bound
HA*(X<Y) ≥ A(X) (A-3)
to the damage in the optimal subtractive overlapping island defense (A*) corresponding to total attack level X and total defense level Y.
We shall now examine certain values for X for which the quantity A(X) is the damage for the optimal terminal defense (B*).
First, consider the B* defense for attack levels X ≤ Xmin(Y). For such attack levels, we have xij ≤ yij for all i,j. Hence
HB*(X,Y) = (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = X) H(x,y)
= (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = X, S) H(x,y)
= A(X) .
Similarly, the same result holds for all attack levels X ≥ Xmax(Y), since for such attack levels we have xij ≥ yij for all i,j.
Hence (A-3) implies that
HA*(X,Y) ≥ HB*(X,Y) (A-4)
for all X ≤ Xmin(Y) and all X ≥ Xmax(Y).
Let us denote the concave hulls of A* and B* damage curves by DA*(X,Y) and DB*(X,Y), respectively. Since the concave hull of the B* damage curve is linear between Xmin(Y) and Xmax(Y) (by the definition of these quantities), (A-4) implies that the A* hull must everywhere exceed the B* hull. Thus
DA*(X,Y) ≥ DB*(X,Y) (A-5)
for all X,Y. The main result of this section is hence proved: the concave hull of the optimal subtractive overlapping island defense (A*) damage curve is bounded below by the concave hull of the optimal terminal defense (B*) damage curve.
We can derive a result somewhat stronger than (A-4) for points X ≤ Xmin(Y). Let us denote the point corresponding to the left end of the linear portion of the A* damage curve by XL. For points X ≤ XL, all damage is due to leakage. Similarly, for points X ≤ Xmin(Y) on the B* damage curve, all damage is due to leakage. Hence for X≤ XM = min (XL,Xmin(Y)), damage is due to leakage on both curves, and the damage curves must coincide over this region. We hence have that
HA*(X,Y) = HB*(X,Y)
for X ≤ XM.
Furthermore, the result (A-5) implies that the linear portion of the hull of the A* damage curve must be tangent to the initial "leakage" portion for a lower attack level X than that at which the linear portion of the hull of the B* damage curve is tangent to the initial leakage portion. Hence XL ≤ Xmin(Y), and so XM = min(XL, Xmin(Y)) = XL. Hence we have
HA*(X,Y) = HB*(X,Y) (A-6)
for X ≤ XL.
We shall now determine a class of points along the linear portion of the hull of the A* damage curve for which the A* damage curve exceeds (or equals) the B* damage curve. Over the linear portion of the hull of the optimal terminal defense damage curve (i.e., for attack levels X satisfying Xmin(Y) ≤ X ≤ Xmax(Y)), the attacker is indifferent to attacking targets at the high or low level, and he does so in any order that allows him to meet (or nearly meet) his total weapon constraint. Consider now a particular point Xh on the linear hull, namely, that point corresponding to the attacker's attacking all of the targets of some defense regions at the high level, and all of the targets of the remaining defense regions at the low level. (Thus Xh is an attainable point on the hull of the damage function, i.e., it is a point of the damage function itself.) Then we have, for the j-th defense zone, either xij ≥ yij or xij ≤ yij for all i. That is, for the point Xh the subtractive condition S holds. Hence we have
HB*(Xh,Y) = (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = Xh) H(x,y)
= (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = Xh, S) H(x,y)
= A(Xh)
≤ HA*(Xh,Y) , (A-7)
i.e., the damage for the A* defense exceeds the damage for the B* defense at the point Xh (a specially chosen attainable point on the hull of the optimal terminal defense damage curve).
The relationship of the concave hull of the optimal subtractive overlapping island defense damage curve to its lower bound (the concave hull of the optimal terminal defense damage curve) is illustrated in Figure A-1.
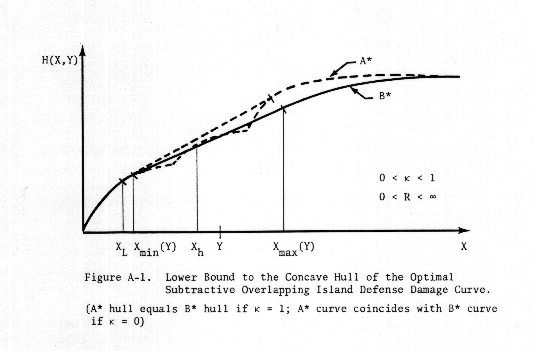
Note that, if all zones are connected, there are
only two points, Xh, namely Xmin(y) and Xmax(Y).
Note also that the results (A-4), (A-6) and (A-7) are stronger conditions than
(A-5), since the former are statements about the A* damage, whereas
(A-7) is a statement about the A* hull.
Note that, since the attacker "moves last," he can in fact choose to attack only at points on the concave hull of the optimal subtractive overlapping island defense curve. Because of this, the fact that the damage curve using subtractive defense can be much lower than the hull appears to be of academic interest. If is of interest to determine the number of points for which the optimal subtractive overlapping island defense damage curve reaches the hull along its linear portion. (The damage curve coincides, with its hull, of course, over the nonlinear portions.) Excluding the two endpoints, this number is (M - 1)M! where M is the number of disconnected collections of connected defense zones (islands). The reasoning behind this number is as follows. Over the linear portion of the hull of the optimal defense curve, the defender will adjust his interceptor allocations, Y, such that disconnected defense regions are equally attractive to the attacker. That is, the marginal damage per weapon after the attacker has "bought into" and "saturated" a region must be the same for all regions (otherwise there would be a succession of linear portions of the damage curve, decreasing slopes, and hence decreasing attractiveness to the attacker). Hence, the attacker is indifferent concerning the order in which he attacks these regions. If there are M disconnected defense regions, then there are M! orderings in which he can attack these regions, and for each ordering, there are M - 1 points on the hull (one for each region, less an endpoint). Hence there are (M - 1)M! points on the hull (assuming that none of the arrangements have points in common).
Particular Cases of Interest
Case 1: κ = 1 (Perfect Interceptors)
For κ = 1, the hulls of A* and B* coincide. This is easily seen by noting that (in the subtractive case) the order in which the attacker fires his weapons into a zone, and hence his deployment of interceptors to targets, has no effect on the damage. At the rightmost point (Xmax(Y)) of the B* damage curve, all interceptors have been exhausted and so condition S holds. Hence we have
HB*(Xmax(Y),Y) = (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = Xmax(Y)) H(x,y)
= (min(y) | Σ(i,j) yij = Y) (max(x) | Σ(i,j) xij = Xmax(Y), S) H(x,y)
= (min(Y) | Σ(j) yij = Yj) (max(y) | Σ(i,j) yij = Y, Σ(i) yij = Yj)
(max(x) | Σ(i,j) xij = Xmax(y), S) H(x,y)
(since damage is affected only by the Yj's, and no the rearrangement within zones)
= HA*(Xmax(Y),Y) .
Case 2: κ = 0 (Completely Unreliable Interceptors)
For κ = 0, either defense (A* or B*) is in fact no defense at all, and so the damage curves coincide (see Figure A-2).

Case 3: Changing Flyout Radius (R) for κ not equal to zero or one
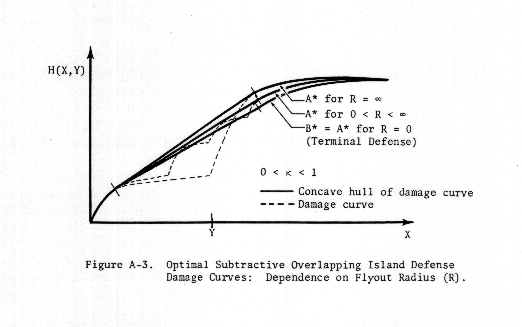
As R approaches zero, we approach the terminal defense case, i.e., the damage curves approach each other. As R approaches infinity, we approach the case of a single island. In general, as R increases, the convexities for A* become wider, but the hull becomes higher (see Figure A-3).
II. Lower Bounds to the Optimal Subtractive Overlapping Island Defense Damage Curve
A. The Leakage Curve
Consider the situation in which an unlimited supply of interceptors is available at each defense zone (island). Since damage is a nonincreasing function of the number of interceptors, an optimal attack against all targets, so defended, cannot result in more damage than the optimal attack against the same targets defended with a finite number of interceptors at each zone. Hence the damage curve for the former situation is a lower bound to the optimal subtractive overlapping island defense damage curve. Since, for targets in defense zones, damage occurs only through leakage (interceptor failure), we shall call this lower bound the "leakage curve" even though it includes (in the region over which the hull is linear) nonleakage damage from undefended targets outside the defense zones.
B. The Perfect Interceptor Curve
In the case of perfect interceptors, the optimal subtractive overlapping island damage curve is completely known. It is simply the no-defense curve, displaced Y units to the right of the origin. This curve is a lower bound to the damage for the optimal curves for any interceptor kill probability κ ≤ 1.
C. The Exhaustion Curve (Approximate Lower Bound)
Consider a particular target set, with a specified set of defense zones (islands). As the flyout radius increases, the "gap" of the optimal subtractive overlapping island defense damage curve becomes wider until the point at which we have a single defense zone and a single gap. The damage curve for this single defense zone lies generally below the damage curves corresponding to smaller flyout radii over the gap, but lies above them on the hull.
An approximation to the single defense zone curve is the perfect interceptor curve, displaced κY units to the right of the origin. This approximation is exact for κ = 0 and κ = 1, but in general seriously underestimates damage for X < Y. It overestimates the damage for X > Y, but not seriously for κ fairly close to 1 (κ = .9 and often κ = .75). How well this curve approximates the actual damage curve is observable for portions of the actual damage curve beyond either end of the linear portion, since we can determine the damage over those regions. If the approximate curve is quite close to the actual damage curve to the right of the linear portion, then it is either quite close to, or below, the actual damage curve over the linear portion. Hence, if the approximate curve is close to the actual damage curve to the right of the linear portion of the actual damage curve, it is a good approximate lower bound.
A "safer" lower bound is obtained by drawing a straight line from the intersection of the approximate curve with the leakage curve to the end of the linear portion of the optimal terminal defense curve. This is a "safer" lower bound since the right endpoint of it is assuredly a lower bound.
It is emphasized that the decision to use this approximate lower bound rests on the "closeness" of the approximate damage curve to the actual damage curve to the right of the linear portion. If the approximate curve is much higher than the actual curve over this region, the approximate lower bound should not be used.
The procedure described above for obtaining the approximate lower bound is illustrated in Figure A-4.

Appendix B: A Generalization of the Exponential Damage Function
I. Expected Damage for the Exponential Damage Function
The following expression for expected damage using the exponential damage function is derived in Lambda Special Report 4, but is included here for completeness of this appendix.
The expected damage on the i-th target if u weapons get through is given by
Di(u) = Pi(1 - exp(-βiu)) .
The probability that u weapons get through, given that there are xi weapons and yi interceptors, both integers, is
A if 0 < u < xi and xi < yi
Pxiyi(u) = 0 if 0 < u < xi-yi and xi > yi
B if xi-yi < u < xi and xi > yi
where
A = C(xi,u)(1 - κ)u κxi - u
and
B = C(yi,(u - (xi - yi))) (1-κ)u - (xi - yi) κxi - u ,
and C(n,e) denotes the combination function (i.e., the number of combinations of n things taken e at a time). (Note: The word processing program used to display this article cannot place subscripts or superscripts on subscripts or superscripts; the exponents xi and yi in the preceding expressions (and in similar expressions that follow) should be xi and yi, respectively.)
The expected damage on the i-th target is hence
Hi(xi,yi) = Σ(u:0,xi) (Expected damage given that u weapons
get through) (Probability that u weapons get
through)
= Σ(u:0,xi) Pi(1 - exp(-βiu))Pxiyi(u)
= PiΣ(u:0,xi) (1 - exp(-βiu))Pxiyi(u)
= PiQi ,
where
A, xi < yi
Qi =
B, xi > yi
where
A = 1 - ((1-κ)exp(-βi)+κ)xi
and
B = 1 - exp(-βi(xi - yi)) ((1 - κ)exp(-βi) + κ)yi .
We shall use this expression for all xi, yi, not just for integral values. We shall simplify the expression for Qi by defining
exp(-αi) = (1 - κ)exp(-βi) + κ
where αi < βi since κ < 1. Hence we have
1 - exp(-αixi) , xi < yi
Qi =
1 - exp(-βi(xi - yi)) exp(-αiyi) , xi > yi .
The total expected damage is
H(x,y) = Σ(i:1,t) Hi(xi,yi)
= Σ(i:1,t) PiQi .
We shall denote the expected damage corresponding to the optimal solutions x*, y* as H(X,Y).
II. Expected Damage for a Damage Function That is a Sum of Exponentials
The analysis of the preceding section follows through mutatis mutandis if we replace the damage function Di(u) by an expression involving a sum of exponentials:
Di(u) = Pi(1 - Σ(t:1,T) ct exp(-bitu) )
where exp(.) denotes the exponential function, i.e., exp(x) = ex where e is the base of natural logarithms.
We obtain
1 - Σ(t:1,T) ct exp(-aitxi) xi ≤ yi
Qi =
1 - Σ(t:1,T) ct exp(-bit(xi - yi) - ai + yi) xi > yi
where ait is defined by
exp(-ait) = (1 - κ) exp(-bit) + κ .
Using this expression for Qi, the analysis for determining the optimal terminal defense goes through as described in Lambda Special Report 4. Some changes must be made to the computer program MINMAX to use such a function, however. A computer program MAX has been written that determines the optimal attack for a specified defense. This program can accept a damage function of the above form with T = 1, 2, or 3.
III. Exponential Approximations to the Square Root Damage Function
A damage function that is widely used is the so-called "square root" damage law:
Di(u) = Pi (1 - (1 - κi sqrt(x)) exp(-κi sqrt(x))
where κi replaces bi as the parameter describing the geographic size of the target, and sqrt(.) denotes the square-root function. The expression for Qi using this formula for Di(u) cannot be put in closed form, and hence the mathematical analysis to determine the optimal damage for the square root law becomes intractable. However, this damage function can be approximated as close as we please by a "sum of exponentials" damage law. Hence we can in essence determine the optimal terminal defense using the square root damage law. The following table gives empirically derived values for the parameters of the expression
Di(u) = Pi (1 - (1 - κi sqrt(x)) exp(-κi sqrt(x))
≈ Pi (1 - Σ(t:1,T) ct exp(-bt κj2 x))
= Pi (1 - Σ(t:1,T) ct exp(-bit x))
where bit = bt κj2.
|
Table B-1. Exponential Approximations to the Square Root Damage Function |
|||||||
|
T |
c1 |
c2 |
c3 |
b1 |
b2 |
b3 |
Maximum Absolute Error 1/ |
|
1 |
1.0 |
0 |
0 |
.219 |
0 |
0 |
.07 |
|
2 |
.561 |
.439 |
0 |
.527 |
.082 |
0 |
.03 |
|
3 |
.492 |
.212 |
.296 |
.172 |
.081 |
.853 |
.01 |
|
1/ For a target of unit value, this is the maximum absolute difference between the square root damage law and the approximation. The c's and b's were chosen so as to (approximately) minimize this quantity. |
|||||||
The "3-term" curve, for all practical purposes, can be considered to coincide with the "square root law" curve.
FndID(216)
FndTitle(Subtractive Overlapping Island Defense with Imperfect Interceptors)
FndDescription(Derivation of the optimal method for allocating attacking missiles and defending interceptors to targets, in the case of subtractive overlapping island defense with imperfect interceptors)
FndKeywords(ballistic missile defense; resource-constrained game; generalized lagrange multipliers)